Новини освіти і науки:

G+

Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция

Явище резонансу і автоколивання

Явище досягнення максимальної амплітуди вимушених коливань при заданих ωо і β називають резонансом. Явище резонансу спостерігається при такій частоті Ω_рез вимушуючої сили, при якій амплітуда вимушених коливань А досягає максимального значення. Відповідно до формули (1.55) дослідження функції A =f(Ω) на екстремум дає рівняння 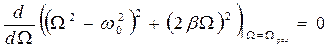, яке дозволяє отримати значення резонансної частоти:

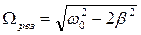Цьому значенню резонансної частоти відповідає значення резонансної максимальної амплітуди

За відсутності затухання (β = 0): Ω_рез = ω₀, а А_рез →.

На мал. 1.25б подані резонансні криві - залежності амплітуди вимушених коливань від частоти змушуючої сили при різних коефіцієнтах затухання (β₁< β₂).

Мал. 1.256. Явище резонансу.

При вимушених коливаннях подача енергії ззовні (для компенсації втрат на тертя) здійснюється і регулюється зовнішньою періодичною силою, яка нав'язує системі свою частоту і визначає амплітуду коливань. Однак, можна викликати незатухаючі коливання І постійною силою, якщо сама система буде регулювати подачу енергії ззовні.

Системи, які автоматично регулюють подачу енергії від зовнішнього джерела, називають автоколивальними, а періодичні процеси, які в них відбуваються, -автоколиваннями. Амплітуда і частота автоколивань залежать від властивостей самої системи. Схему автоколивальної системи, яка складається з чотирьох обов'язкових елементів, подано на мал. 1.26.

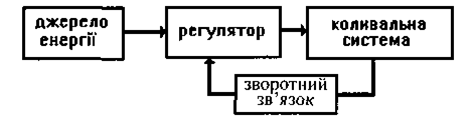
Мал. 1.26. Автоколивальна система.

Прикладами автоколивальних систем є:

1. Годинник (маятник - коливальна система, піднесена гиря або пружина - джерело енергії, анкер-регулятор надходження енергії від джерела в коливальну систему, який зв'язаний з коливальною системою зворотним зв'язком).

2. Генератор електромагнітних коливань.

3. Серце, легені - біологічні автоколивальні системи. Форма автоколивань може бути різною: це можуть бути

коливання, що наближаються до гармонічних (маятниковий годинник, коливання в LC-генераторах), або імпульсні коливання різної форми - прямокутні, експоненціальні, пилкоподібні.

1.3.5. Додавання гармонічних коливань

Коливання, для котрих зміщення як функція часу може бути описано будь-яким законом, окрім синуса чи косинуса, називають складними (негармонічними).

Відомо, що будь-яке складне коливання можна подати у вигляді суми простих гармонічних коливань. Перш ніж аналізувати складні коливання (а таку задачу медикам доводиться розв'язувати досить часто), розглянемо, до яких результатів може призвести додавання гармонічних коливань.

1. Додавання гармонічних коливань, спрямованих вздовж однієї прямої

Нехай тіло бере участь одночасно у двох коливаннях, спрямованих вздовж однієї прямої, причому амплітуди і періоди (частоти) цих коливань однакові, а початкові фази різні

Результуюче зміщення х тіла від положення рівноваги дорівнює алгебраїчній сумі зміщень х₁ і х₂:

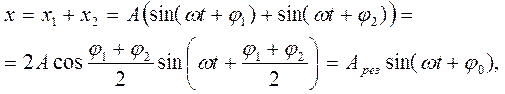де

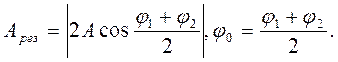
Таким чином, результуюче коливання являє собою гармонічне коливання, яке відбувається вздовж тієї ж самої прямої, що і складові коливання, і з періодом (частотою), який дорівнює періоду (частоті) складових коливань. Амплітуда результуючого коливання залежить від різниці початкових фаз складових коливань. Якщо φ₁ -φ₂ = 2kπ , де k= 0, 1,2, ...,то 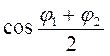= ±1 і А_рез = 2А (або А_рез = А₁+A₂, якщо A₁≠ А₂). Якщо φ₁- φ₂ = (2k + 1)π, то

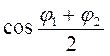= 0 і А_рез= 0 (або А_рез = А₁-A₂, якщо A₁≠ А₂ ).

Якщо складові коливання відрізняються періодами (частотами), то результуюче коливання вже не буде гармонічним. Розглянемо, як особливо цікавий, результат додавання двох гармонічних коливань рівних амплітуд і фаз, періоди (частоти) яких відрізняються, тобто

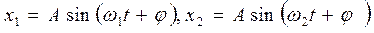Результуюче зміщення дорівнює

де .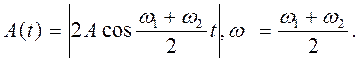

Якщо різниця ω₁-ω₂ мала, то амплітуда A(t) змінюється з часом за гармонічним законом, але з частотою 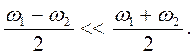Такі коливання називають биттям (мал. 1.27).

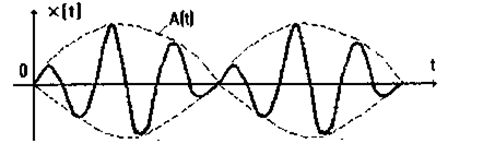
Мал. 1.27. Биття.

Період зміни амплітуди коливань називають періодом биття (Т_б). Період биття може бути визначений з умови:

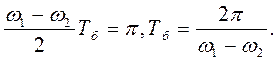Отже, частота 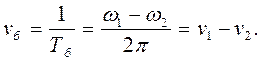. Таким чином,

частота зміни амплітуди результуючого коливання дорівнює різниці частот складових коливань.

2. Додавання взаємноперпендикулярних гармонічних коливань

Нехай матеріальна точка водночас бере участь у двох коливаннях, що відбуваються у взаємно перпендикулярних напрямках:

Сукупність координат х і у матеріальної точки у різні моменти часу визначають траєкторію руху матеріальної

точки у площині XY. Форма траєкторії залежить від співвідношення частот і різниці фаз складових коливань. Наведемо деякі випадки додавання коливань (мал. 1.28):

1) ,

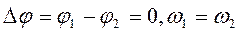рівняння траєкторії ;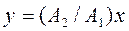

2) ,

рівняння траєкторії ;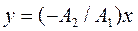

3) , рівняння траєкторії ;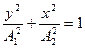

4, 5) 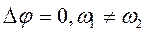, у цьому випадку форма траєкторії залежить від співвідношення частот ω₁ і ω₂. На мал. 1.28 наведено траєкторії для випадків ω₁:ω₂=1:2 і ω₁: ω₂= 2:3.

Мал. 1.28. Складання взаємно перпендикулярних коливань (фігури Лісажу).

Отримані криві, що їх описує матеріальна точка, називають фігурами Лісажу. Криві, подібні до кривих Лісажу, спостерігають при дослідженні біопотенціалів серця методом векторелектрокардіографії.

Читайте також:

<== попередня сторінка	\|	наступна сторінка ==>
Вимушені коливання	\|	МЕХАНІЧНІ ХВИЛІ

Не знайшли потрібну інформацію? Скористайтесь пошуком google:

Генерація сторінки за: 0.004 сек.