• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Принцип відповідності

Принцип відповідності є одним з фундаментальних методологічних принципів сучасної квантової фізики, який в гносеологічному плані в повній мірі відображує аспект матеріальної єдності фізичної картини світу, необхідності розгляду фізики як цілісної науки з урахуванням зміни її якісних станів на різних стадіях розвитку.

Саме принцип відповідності забезпечив вирішальний внесок у створення квантової механіки як на першій стадії (1900-1920 рр.), і продовжує відігравати провідну роль у її подальшому розвитку (з 20-х років минулого сторіччя і дотепер).

Найбільш узагальненим вважається визначення принципу відповідності, здійснене І.В.Кузнецовим як „…теорії, справедливість якої була експериментально встановлена для певної групи явищ; з появою нової теорії не відкидаються, але зберігають своє значення для попередньої області явищ як гранична форма та частковий випадок нових теорій” [44].

Методологічна цінність принципу відповідності у наведеній трактовці полягає в тому, що І.В.Кузнецов співставляє подібність дії принципу відповідності в історії розвитку фізики з особливостями розвитку математичного знання, стверджуючи: „Математичний апарат нової теорії, яка містить деякий характеристичний параметр, значення якого є різним у старій та новій областях явищ, при належному значенні характеристичного параметра переходить у математичний апарат старої теорії”[44].

Підтвердимо зазначене рядом прикладів з історії розвитку сучасної науки, а отже й відповідних стадій формування принципу відповідності. В межах класичної фізики (оптики) одним з перших проявів принципу відповідності є співвідношення поміж хвильовою оптикоюта їїпопередницею геометричною оптикою, яка є граничним випадком хвильової оптики, при якому нехтується кінцеве значення довжини світлової хвилі (l ~ 10^–7 м), тобто вважається, що l ® 0 або хвильовий вектор . Такий наближений підхід має місце за умови, коли геометричні розміри d предметів, які огинаються світловими хвилями та відстані r до цих предметів значно перевищують довжину хвиль l, тобто при .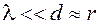

Отже характеристичними параметрами хвильової оптики є довжина хвилі 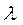або хвильовий вектор 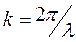. І саме при певних значеннях цих параметрів відбувається перехід поміж теоріями.

Як зазначають автори фундаментальної монографії [58], найближчим історичним попередником принципу відповідності у наведеному його визначенні є відповідний аналіз своєї квантової гіпотези теплового випромінювання, проведений М.Планком у 1906 році.

Неодноразові спроби пояснити закони теплового випромінювання методами класичної теоретичної фізики (термодинаміки, електродинаміки, статичної фізики) переконливо довели хибність такого підходу, оскільки теоретичні висновки були в явному протиріччі з принципом збереження енергії. Теоретичне обґрунтування спектральних закономірностей випромінювання абсолютно чорного тіла в усьому інтервалі частот вперше вдалося здійснити М. Планку. Саме він, розглядаючи випромінюючу систему як сукупність лінійних гармонічних осциляторів з різними власними частотами ν, першим запропонував дискретність енергії цих осциляторів 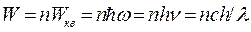, де п = 0, 1, 2, 3, …

При цьому квант енергії (елементарна порція) пропорційний частоті

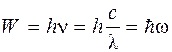, (2.1)

де h = 6,626 ∙ 10^–34 Дж ∙ с та 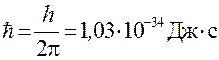– універсальна стала (стала Планка), квант дії, а ω = 2πν – циклічна частота.

Саме на підставі такої квантової гіпотези М. Планк після декількох років праці отримав формулу для спектральної випромінювальної здатності абсолютно чорного тіла r або об’ємної ρ спектральної здатності, яка визначалася через квант енергії h .

Гіпотеза М. Планка була певною мірою обмеженою, бо ґрунтувалася на емпіричній формулі. До того ж, М. Планк наполягав, що корпускулярний, квантовий характер випромінювання чи поглинання відбувається лише безпосередньо поблизу тіла, а на відстані від тіла (у просторі) це випромінювання є виключно хвильовим. Отже, М. Планк не вірив у реальність існування квантів світла (фотонів) поза межами тіла, у просторі.

Проте саме гіпотеза М. Планка про квантову корпускулярну природу процесу випромінювання абсолютно чорного тіла стала основою для створення сучасної квантової теорії.

На підставі теорії М. Планка можна довести експериментальні закони теплового випромінювання (закон Стефана-Бальмана та закон зміщення Віна), оскільки спектральна випромінювальна здатність r ( , T) за квантовою теорією співпадає з експериментом в усьому інтервалі частот ν від 0 до ∞, на відміну від спектральної випромінювальної здатності за класичною теорією, яка ґрунтувалася на хвильовій природі теплового випромінювання і узгоджувалася з експериментом лише в інтервалі малих частот (так звана УФ-катастрофа).

Не важко переконатися, що при h 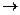0 спостерігається відповідність поміж квантовими та класичними висновками. Отже характеристичним параметром в даному випадку є квант дії h або 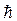, який має різні значення в квантовій ( 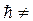0) та класичний (h 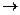0) теоріях.

Аналізуючи еволюцію понять квантової механіки М. Джеммер [24] зазначає, що термін „відповідність” як terminus technicus вперше був використаний Н. Бором у його статті „Про серіальні спектри елементів” у такому вигляді: „Природа цієї відповідності саме така, що справжню теорію спектрів в певному сенсі слід розглядати як раціональне узагальнення звичайної теорії випромінювання”.

Лінійчатий спектр випромінювання атомів чи ядер зумовлений дискретністю їх енергетичного спектру, тобто квантованними значеннями енергії Wn (енергетичними рівнями), які визначаються головним квантовим числом n (n = 1, 2, 3… ).

Залежність квантування енергії Wn від величини квантового числа n можна представити у вигляді співвідношення: ,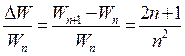

яке при значному збільшенні числа n, набуває виду 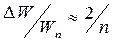[109].

Отже, при великих значеннях n величина різниці сусідніх енергетичних рівнів 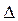W стає малою у порівнянні з Wn (енергією кожного з рівнів). Відбувається зближення енергетичних рівнів, вони стають квазібезперервними. Завдяки цьому маємо результати близькі до результатів класичної теорії.

Характеристичним параметром відповідності поміж квантовою та класичною теоріями є головне квантове число n. Тому принцип відповідності був сформульований Н. Бором у такому вигляді: при значних за величиною значеннях квантових чисел висновки та результати квантової механіки повинні бути відповідними до класичних результатів.

Е. Віхман, розглядаючи зміст принципу відповідності Н. Бора як „ідею про те, що класичну механіку слід вважати граничним випадком квантової механіки” [15], зауважує, що саме принцип відповідності за своєю суттю ставить під сумнів вибір правил „квантування” в якості своєрідного дороговказу на вибір напрямків переходу від класичного засобу описання до квантово-механічного.

При цьому Е. Віхман вважає, що характеристичними параметрами для переходу поміж квантовою механікою і класичною (граничним випадком квантовою) є невизначеність координат та проекцій імпульсу класичних чи квантових об’єктів.

При цьому класична та квантова механіки стають еквівалентними теоріями за умови, що невизначеністю зазначених характеристичних параметрів можна знехтувати.

Близьким за формою, але більш деталізованим у порівнянні з визначенням Е. Віхмана [12] є визначення принципу відповідності у підручнику Л.Д. Ландау та Є.М. Ліфшица [47], що поданий у такому вигляді: „Квантова механіка займає досить своєрідне місце серед фізичних теорій – вона містить класичну механіку як свій граничний випадок і в той же час відчуває потребу в останньому задля свого власного обґрунтування” [47].

Проте Маріо Бунге не погоджується з таким визначенням, вважаючи, що квантова механіка не охоплює класичну механіку в цілому, а містить лише крихітний її фрагмент [11].

Спробуємо переконатися в цьому на хрестоматійному прикладі по визначенню відповідності поміж класичною механікою, тобто механікою відносно малих за величиною швидкостей (ν << с = 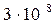м/с), та релятивістською механікою (ν 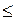с = 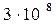м/с), яка описується спеціальною теорією відносності (СТВ), постулатам якої спроможні задовольнити лише перетворення Лоренца для координат та часу поміж двома інерціальними системами відліку – нерухомою ( 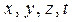) та системою ( 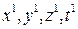), що рухається з швидкістю .

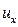Не важко довести [60], що ці перетворення мають такий вигляд:

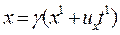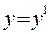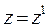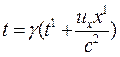; ; ; , (2.2)

де 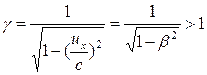– співмножник Лоренца.

Характеристичним параметром для переходу поміж релятивістською та класичною механіками є співвідношення швидкостіруху 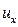дошвидкості с= 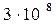м/с, а саме.

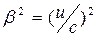Якщо 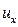<< 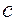, тобто 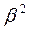<<1 та 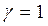маємо перетворення Галілея (класична механіка) як граничний випадок більш узагальнених перетворень Лоренца.

Згідно принципу відповідності з релятивістського закону додавання швидкостей [50] маємо в якості граничного випадку при класичний закон додавання швидкостей: ( ).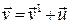

Аналогічно релятивістське визначення кінетичної енергії: як різниці повної енергії 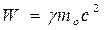, та енергії спокою 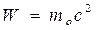, релятивістського імпульсу 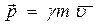, релятивістської сили 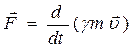повністю співпадають з їх визначеннями у класичній механіці за умови, щ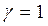о або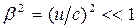

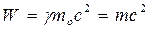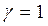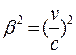Проте співвідношення для повної енергії , всупереч принципу відповідності не має свого граничного випадку, класичного аналогу навіть при або << 1.

Кінетична енергія як у релятивістській механіці, так і у класичній має однаковий фізичний зміст, як енергія, що зумовлена рухом будь-якого об’єкту (класичного чи квантового) з швидкістю . Але при цьому існує істотна різниця, оскільки у класичній механіці кінетична енергія спокою ( 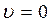) дорівнює нулю, а у релятивістській механіці маємо енергію спокою не рівну нулю .

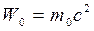Більш узагальненою теорією простору-часу у порівнянні з спеціальною теорією відносності (СТВ), є загальна теорія відносності (ЗТВ), яка охоплює не тільки інерціальні системи відліку ( 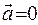), але й неінерціальні системи, що рухаються з прискоренням ( ).

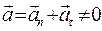Виходячи з принципу еквівалентності поля сил інерції, зумовлених прискоренням та сил тяжіння. А. Ейнштейн довів, що зазначена еквівалентність спостерігається за рахунок викривлення простору – часу (СТВ), інваріантною абсолютною величиною для якого є просторово-часовий інтервал S 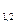поміж двома подіями:

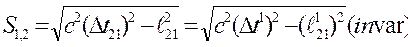, де 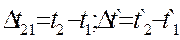– проміжки часу, а 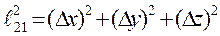; 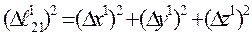– відстань поміж точками ізотропного однорідного простору різних неінерціальних систем відліку [60].

Отже ЗТВ розглядає іншу модель Всесвіту (неоднорідного та неізотропного), як викривленого чотиривимірного простору-часу, який змінюється залежно від розподілу матерії.

Для будь-якого виду матерії (фізичного вакууму, поля, плазми, речовини) подібне викривлення неевклідового простору-часу залежить від різноділу матерії, тобто визначається не лише величиною мас m, але й всіма видами енергії, які властиві матеріальним об’єктам.

Вплив будь-якого з зазначених видів матерії на властивості, метрику такого просторово-часового континіуму описується універсальною гравітаційного сталою 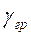, яка є коефіцієнтом зв'язку простору-часу з середовищем.

При цьому взаємозв’язок поміж гравітаційними універсальними сталими у класичній та релятивістській теорії описується співвідношенням

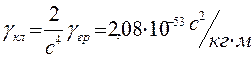
При слабких полях та відносно малих швидкостях 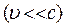рівняння ЗТВ співпадають з рівняннями класичної теорії тяжіння.

Таким чином згідно зметодологічним принципом відповідності попередня (за часом появи) класична теорія тяжіння І. Ньютона є окремим випадком більш узагальнених релятивістських теорій гравітації, зокрема загальної теорії відносності (ЗТВ). Характеристичним параметром переходу поміж теоріями і в цьому випадку є .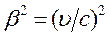

Принцип відповідності стає в нагоді і при з’ясованій проблеми законів збереження енергії в загальній теорії відносності (ЗТВ). При цьому існують протилежні точки зору на цю проблему: від твердження про відсутність взагалі такої проблеми до песимістичних прогнозів про надзвичайну складність теоретичною розв’язання зазначеної проблеми.

Не зупиняючись на детальному аналізі цих точок зору, вважаємо за доцільне зупинитися на одному з варіантів підходу до законів збереження енергії, імпульсу та моменту імпульсу в ЗТВ, викладеному в статті [20], автор якої спирається на принцип відповідності.

Підставою для цього є те, що класична нерелятивістська механіка є початковим (логічним та історичним) пунктом та граничним випадком для релятивістської механіки (СТВ), яка в свою чергу повинна бути граничним випадком для ЗТВ за умови визначення тих фізичних величин і властивостей СТВ, що можуть бути узагальнені в ЗТВ.

Такимабсолютним елементом в ЗТВ, як показано в [20] є розмірність простору-часу, однакова для всіх його точок подібно до просторово-часового інтервалу 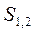в СТВ. При цьому розмірностна однорідність виражається симетрією квазигрупового характеру і чотиривимірна геометрія простору-часу задається функцією восьми змінних, яка визначає інтервал поміж двома довільними точками через інтервали від цих точок до чотирьох фіксованих точок [20]. Саме з такою квазигрупною структурою і слід асоціювати закони збереження в ЗТВ.

Надзвичайно важливо, що згідно з принципом відповідності введене для опису викривленого простору-часу 10-параметрове сімейство з квазигрупною структурою (метрика ЗТВ) переходить в граничному випадку в групу Пуанкаре, з якою асоціюються закони збереження в СТВ.

Отже, спираючись на принцип відповідності та виходячи з безпосереднього взаємозв’язку законів збереження з відповідними симетріями простору-часу [11] можна стверджувати, що у ЗТВ має місце узагальнений закон збереження енергії – імпульсу – моменту імпульсу, тобто поодинці закон збереження енергії-імпульсу та закон збереження моменту імпульсу втрачають свій інваріантний зміст.

Подібна відповідність спостерігається, і в релятивістській СТВ, де енергія та імпульс поодинці теж втрачають свій інваріантний зміст, який вони мали в класичній, нерелятивістській механіці (СТВ), тобто має місце узагальнений закон збереження енергії-імпульсу.

Принцип відповідності є невід’ємною складовою сучасного наукового пізнання, однієї з найбільш важливих форм переходу від існуючої теорії (з певними обмеженнями та протиріччями) до більш узагальненої теорії. Такий перехід передбачає не тільки уточнення основних математичних співвідношень, якими описується існуюча реальність, але введення та подальше використання нових уявлень, та понять. В цьому і полягає методологічна та гносеологічна роль принципу відповідності не тільки в процесі визначення взаємозв’язку поміж науковими теоріями, але й поміж окремими стилями мислення. Отже і розвиток теоретичного мислення на його різних стадіях відбувається згідно принципу відповідності.

Слід пам’ятати, що механізм переходу поміж фундаментальними теоріями „…не вичерпується лише принципом відповідності, а саме відношення відповідності є далеко не елементарним, а, напроти, досить комплексним відношенням” [58].

Подібні погляди щодо принципу відповідності висловлює і відомий філософ Р.А. Аронов, котрий зазначає „…вірно в цьому принципі лише те, що старі теорії зберігають своє значення для попередньої області явищ. Все ж інше, про що йде в ньому мова, потребує певної корекції. В основному математичний апарат квантової механіки дійсно переходить в математичний апарат класичної фізики при h 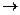0 (де h – стала М. Планка). Проте, наприклад, принцип суперпозиції хвильових функцій ніяким чином не зачіпається цим граничним переходом” [2], як не має свого класичного аналізу і співвідношення для повної енергії .

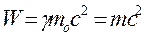При цьому, посилаючись на свої попередні статті, автор не розділяє точку зору про те, що існуючі старі теорії можуть зберегти своє значення для попередньої області в якості „часткового випадку нових теорій”. Завдяки тому, що „ні очі, ні нерви, ні мозок суб’єкта-спостерігача не володіють квантовими властивостями і не підпорядковуються законам квантової механіки, наближеним виявляється лише граничний перехід запропонованого автором статті [56] їх квантово-механічного опису при h 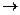0, але аж ніяк не класичний опис їх поведінки” [2].

Таким чином, кінцеві висновки більш сучасних теорій (квантової та релятивістських механік) не в повному обсязі співпадають з висновками класичної механіки завдяки наявності зазначених невідповідностей.

Отже принцип відповідності, як найбільш суттєва форма переходу від існуючих до більш сучасних нових теорій є необхідною, але недостатньою умовою істинності нової, більш узагальненої теорії.

Принцип відповідності може бутизастосований лише за умови наявності певної відповідності поміж двома теоретичними системами, які стосуються однієї предметної області, що досліджують один і той же об’єкт „з різним ступенем глибини аналізу на рівні системи” або підсистеми. Отже, між об’єктами теорії, які розглядаються, повинна існувати певна структурна та матеріальна спільність. При цьому не тільки більш сучасна стадія розвитку зберігає ознаку свого минулого, але й саме минуле в певній мірі „передбачає” майбутнє. Саме за таких умов „відношення граничного переходу, існуюче поміж теоріями, які змінюють одне одну і стосуються однієї і тієї ж предметної області, набуває необхідного евристичного характеру” [58].

Саме наявність зазначених умов і є підґрунтям для формулювання принципу відповідності як узагальненої методологічної вимоги. Зокрема, в класичній фізиці співвідношення поміж термодинамікою та статистичною фізикою, як більш глибокою теорією (у порівнянні з термодинамікою) щодо одних і тих же явищ, не є наслідком принципу відповідності [11, 85]. Причинами цього є невиконання вимог граничного переходу поміж цими теоріями, наявність яких і є обов’язковою умовою застосування принципу відповідності.

Тим не менш, термодинаміка має певні переваги перед статистичною фізикою і більш широко застосовується. Маріо Бунге не виключає „можливість певного регресу, коли на місце сучасних теорій можуть прийти нові, більш низького рівня…” [11]. Хоча автор передбачає і у майбутньому наявність вже існуючих відношень поміж теоріями у досить різноманітному їх варіанті, а саме якметодологічні та евристичні.

При цьому методологічні відношення М. Бунге розподіляє на такі дві різновидності:

1) першого роду, коли одна теорія є по суті лише інструментом, за допомогою якого відбувається пошук та вибір можливих експериментальних перевірок іншої теорії;

2) другого роду, якщо попередня теорія розглядається в якості необхідної умови, якій повинна задовольнити наступна теорія, здебільшого в певному граничному випадку.

Евристичні відношення характерні на стадії виникнення нової теорії, коли принципи її побудови здебільшого не є очевидними і витікають в певній мірі з основ та протиріч попередньої існуючої теорії. При цьому принцип відповідності має важливе самостійне евристичне значення.

Переконливим підтвердженням такої евристичності відношень є зокрема відношення між класичними квантовими теоріями електропровідності та теплопровідності.

Самостійне евристичне значення принцип відповідності (як своєрідний селектор можливих нових наукових гіпотез та принципів побудові більш сучасної наступної теорії) має саме на стадії виникнення нової теорії з обов’язковим доказом існування граничного переходу поміж теоріями.

При цьому, слід розрізняти суттєву відміну поміж узагальненим відношенням граничного переходу в розвитку математичного знання та принципом відповідності в фізиці, незважаючи на їх певну схожість.

При формальному підході результат переходу математичного апарату більш сучасних теорій може розглядатися як гранична форма та частковий випадок. Але при цьому не враховується суттєва відмінність формального та змістовного аспектів граничного переходу, а саме те, що за змістом граничний перехід є насправді не лише кількісним, а перш за все якісним переходом.

Не можна розглядати класичну фізику як граничний випадок квантової або релятивістської фізики, оскільки класична фізика має інший зміст неквантової та нерелятивістської фізики, яка розглядає змістовно іншу фізичну реальність.

Для математичних понять, як і для природознавчих наукових понять(зокрема понять фізики), існують царини їх застосування, за межами яких усім цим поняттям не відповідає будь-що справжнє реальне.

Досить нагадати, що геометрія викривленого простору-часу, створена Лобачевським і Ріманом та висновки загальної теорії відносності А.Ейнштейна як сучасної теорії тяжіння, охоплюють просторово-часові масштаби, де домінуючу роль має гравітаційна взаємодія, а геометрія плоского простору Евкліда обмежується просторово-часовою цариною, де головну роль відіграє електромагнітна взаємодія.

Отже, математичні і фізичні поняття є відповідними образами однієї і тієї ж реальності, причому саме образами, а не ознаками чи символами, оскільки в підсумку дозволяють отримати один і той же елемент наукового знання. Реалістичність математики, як і будь-якої іншої природознавчої науки, полягають в тому, що вони являють собою певний фрагмент теоретичної конструкції однієї й тієї ж реальної дійсності.

Ще Арістотель прозорливо відзначав, що корні абстрактних математичних понять заглиблені в реальному світі.Розділяв подібні погляди і А.Ейнштейн, який був переконаний в тому, що саме завдяки „математичним конструкціям можливо визначити ті фізичні поняття та існуючі закономірні взаємозв’язки поміж ними, які дають підстави до з’ясування суті явищ природи”.

В зв’язку з цим, як наполягає Р.І.Аронов, потрібне уточнення змісту принципу відповідності, який розглядає класичну фізику не у вигляді часткового випадку квантової чи релятивістської, тобто за відсутності розмежування поміж галузями застосування зазначених фізик. Принцип відповідності передбачає існування межі поміж галузями застосування класичної та квантової чи релятивістської фізики, але завдяки певній кореляції поміж цими областями ця межа є досить прозорою щодо взаємного проникнення, тобто виконує одночасно функції певного їх відділення і засобу їх своєрідного взаємозв’язку.

Як зазначають автори монографії [58] „відношення граничного переходу стосується математичного каркасу” теорії, а принцип відповідності – перш за все області предметної інтерпретації, екстенсивного розповсюдження засобу інтерпретації нової моделі на галузь інтерпретації попередньої моделі.

Отже, перш за все, предметна змістовність фізичних теорій зумовила перетворення граничного переходу саме в відношення відповідності. Так, перетворення Лоренца з допоміжним математичним поняттям місцевого часу, характерного для різних систем відліку, так би і залишилися прикладом граничного переходу поміж формулами релятивістської та класичної механіки, якби А. Ейнштейн не здійснив корінну перебудову уявлень про простір та час (форми існування матерії), запропонувавши чотиримірний простір-час.

Завдяки цьому вникла якісно нова фізична теорія простору-часу, яка узагальнювала попередню класичну теорію згідно вимогам принципу відповідності. Евристичність цього принципу полягає в тому, що він завдяки новим предметним поняттям, категоріям та їх відповідної інтерпретації не тільки значно „розширює” межі застосування більш сучасної теорії, але й зберігає попередню теорію в якості окремого, більш „звуженого”, наближеного випадку. Отже, попередня теорія залишається „відносною істиною, тобто абсолютною істиною у певних межах” [49].

Тому цілком природно, що в переважній більшості праць філософів чи фізиків, з’ясовуючих суть та значення принципу відповідності, цей принцип аналізується в контексті теорії істини. При цьому надзвичайно важливо не обмежуватися пошуками дійсно існуючого взаємозв’язку поміж принципом відповідності та загально-філософським положенням про діалектику відносної та абсолютної істини, але й аналізувати ті відмінності, які існують між ними.

Узагальнено-методологічний філософський принцип (положення) щодо взаємозв’язку відносної та абсолютної істини є більш універсальним, тобто розповсюджується на зміну найбільш фундаментальних теоретичних уявлень, характеризує розвиток узагальненого наукового знання про об’єктивну дійсність. Тому для таких узагальнених форм розвитку знань не можуть бути застосовані не тільки відношення граничного переходу, але й відношення відповідності.

Принцип відповідності ґрунтується на відношеннях поміж теоріями лише певної предметної спрямованості. Тому він не може претендувати на роль узагальнено-філософського принципу.

Отже, принцип відповідності є підтвердженням узагальненого методологічного положення про взаємозв’язок відносної та абсолютної істинивиключно в межах певної області знань, характеризуючи співвідношення, які виникають поміж теоріями, що стосуються будь-якої, але однієї сфери реальності.

Розвиток таких теорій являє собою закономірний перехід від одного рівня аналізу суті фізичних явищ до більш поглибленого. При цьому будь-яка логічно замкнена теорія (наприклад класична чи квантова механіка) є лише певною сходинкою, щаблем процесу пізнання об’єктивної реальності в межах, охоплюваних цією теорією. Процес пізнання йде шляхом певного заперечення, усунення або замін попередніх теоретичних систем іншими, але при обов’язковому врахуванні, збереженні позитивних здобутків теорії-попередниці.

Спадкоємний зв’язок поміж теоріями полягає в тому, що фізичні уявлення, поняття і навіть принципи теорії-попередниці використовуються в подальшій теорії в більш „удосконаленому”, а можливо, і новому тлумаченні. Отже, основні конструктивні елементи теоретичних систем зберігаються. Суттєво, щоб нові універсальні фізичні теорії, які більш повно відображають властивості матерії, мали в свою чергу певний запас можливостей їх подальшого удосконалення на якісно новому, більш глибокому рівні наукового пізнання.

Принцип відповідності об’єктивно спрямовує дослідника проти спроб зведення зазначених теорій в ранг абсолютної істини, проти абсолютизації тих положень та уявлень, на яких ґрунтується будь-яка теоретична система. При цьому специфіка принципу відповідності, зумовлена особливими умовами за яких він діє, не дозволяє вважати цей принцип як автоматичний наслідок філософської тези про взаємозв’язок абсолютної та відносної істини.

Принцип відповідності має гносеологічне та евристичне значення в межах окремих наук, тому поступаючись в узагальненості філософському положенню про відносну та абсолютну істину, цей принцип суттєво виграє в конкретності визначення алгоритмів побудови нової фізичної теорії, шляхів та варіантів її вибору.

Отже, принцип відповідності, як і інші методологічні принципи окремих наук, здатні до виходу „за межі гносеологічних положень загальної філософської теорії. Так, принцип відповідності не тільки може бути інтерпретований як прояв діалектики абсолютної та відносної істини в процесі пізнання, але й свідчить також на користь онтологічного статусу нової теорії і тому може розглядатися як важливий доказ на користь об’єктивної істинності теоретичного пізнання” [58].

Слід підкреслити, що в гносеологічному значенні принцип відповідності розкриває певний аспект матеріальної єдності всесвіту, взаємозв'язку фізичних явищ, надає можливість переконатися на підставі аналізу різних фізичних картин світу та стадій розвитку фізичної науки в тому, що фізика повинна розглядатися як єдина цілісна наука.

Принцип відповідності є методологічним орієнтиром для побудови та подальшого критичного співставлення різних наукових теорій в їх взаємозв’язку, єдності та подальшому розвитку.

На певній стадії розвитку квантової механіки Н. Бор вважав принцип відповідності виключно законом квантової теорії, стверджуючи, що „увесь апарат квантової механіки можна розглядати як точне формулювання тенденцій, закладених в принципі відповідності”. Дійсно, саме цей принцип став вирішальним внеском в зусилля багатьох фізиків по створенню квантової механіки.

Проте методологічне значення принципу відповідності на сучасному етапі розвитку науки виходить за межі квантової механіки, і саме цей принцип є гносеологічним орієнтиром в процесі наукового пізнання. Аналізуючи еволюцію понять квантової механіки та особливості співвідношень поміж квантовою та класичною механіками, М. Джеммер зазначає, що „…формалізм (мова) квантової механіки, які з концептуальної точки зору найбільш радикальним чином відрізняються від формалізму класичної…, незважаючи на це і нібито охоплює останню у вигляді окремого випадку, як це й стверджує принцип відповідності в його звичному формулюванні” [24].

Переконливим доказом цього є, зокрема, принцип невизначеності, один з найбільш важливих методологічних принципів квантової механіки.

Але перед цим слід підкреслити, що на існуючій стадії розвитку сучасної науки методологічне знання принципу відповідності не обмежується виключно квантовою механікою. Саме цей принцип став надійним гносеологічним орієнтиром в процесі виникнення, створення нових гіпотез, концепцій, теоретичних моделей, як існуючих, так і тих, що будуть виникати в майбутньому і поза межами природознавчих наук.

Читайте також:

1. Аграрна політика як складова економічної політики держави. Сут­ність і принципи аграрної політики
2. Адекватна реалізація принципів міжнародної економіки можлива лише в стабільному політичному середовищі.
3. Адміністративна відповідальність: поняття, мета, функції, принципи та ознаки.
4. Адміністративні методи - це сукупність прийомів, впливів, заснованих на використанні об'єктивних організаційних відносин між людьми та загальноорганізаційних принципів управління.
5. Алкмеон. Принцип нервізма. Нейропсіхізм. Принцип подібності
6. Аналіз отриманих результатів, прийняття рішення про можливість видачі сертифікату відповідності
7. Аналогія права - вирішення справи або окремого юридичного питання на основі принципів права, загальних засад і значення законодавства.
8. Антикорупційні принципи
9. Антикорупційні принципи
10. Антикорупційні принципи
11. Антикорупційні принципи
12. Антропологічний принцип філософії Л. Фейербаха

Переглядів: 3161