
РЕЗОЛЮЦІЯ: Громадського обговорення навчальної програми статевого виховання
ЧОМУ ФОНД ОЛЕНИ ПІНЧУК І МОЗ УКРАЇНИ ПРОПАГУЮТЬ "СЕКСУАЛЬНІ УРОКИ"
ЕКЗИСТЕНЦІЙНО-ПСИХОЛОГІЧНІ ОСНОВИ ПОРУШЕННЯ СТАТЕВОЇ ІДЕНТИЧНОСТІ ПІДЛІТКІВ
Батьківський, громадянський рух в Україні закликає МОН зупинити тотальну сексуалізацію дітей і підлітків
Відкрите звернення Міністру освіти й науки України - Гриневич Лілії Михайлівні
Представництво українського жіноцтва в ООН: низький рівень культури спілкування в соціальних мережах
Гендерна антидискримінаційна експертиза може зробити нас моральними рабами
ЛІВИЙ МАРКСИЗМ У НОВИХ ПІДРУЧНИКАХ ДЛЯ ШКОЛЯРІВ
ВІДКРИТА ЗАЯВА на підтримку позиції Ганни Турчинової та права кожної людини на свободу думки, світогляду та вираження поглядів
- Гідрологія і Гідрометрія
- Господарське право
- Економіка будівництва
- Економіка природокористування
- Економічна теорія
- Земельне право
- Історія України
- Кримінально виконавче право
- Медична радіологія
- Методи аналізу
- Міжнародне приватне право
- Міжнародний маркетинг
- Основи екології
- Предмет Політологія
- Соціальне страхування
- Технічні засоби організації дорожнього руху
- Товарознавство продовольчих товарів
Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция
Принцип невизначеностей
Цей принцип, введений одним з творців квантової механіки В. Гейзенбергом, ґрунтується на співвідношенні невизначеностей для координат (х, у, z) та відповідних проекцій імпульсу 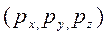 будь-якого квантового мікрооб’єкту. Тому в деяких літературних джерелах обмежуються саме аналізом зазначених співвідношень невизначеностей без розкриття методологічного їх значення на рівні відповідного принципу. Спробуємо довести обмеженість такого підходу.
будь-якого квантового мікрооб’єкту. Тому в деяких літературних джерелах обмежуються саме аналізом зазначених співвідношень невизначеностей без розкриття методологічного їх значення на рівні відповідного принципу. Спробуємо довести обмеженість такого підходу.
Вирішальним для створення квантової механіки в цілому і співвідношення невизначеностей зокрема, стала гіпотеза (теорія) Луі де Бройля про корпускулярно-хвильовий дуалізм, двоєдиність всіх без винятку матеріальних об’єктів мікросвіту чи макросвіту.
Суть гіпотези зводилася до того, що дуалізм є особливістю не тільки фотонів (квантів випромінювання) з енергією 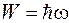 та імпульсом
та імпульсом 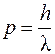 , але й має універсальне значення, розповсюджується на всі без винятку матеріальні об’єкти.
, але й має універсальне значення, розповсюджується на всі без винятку матеріальні об’єкти.
Отже, нерелятивістській рух будь-якого мікрооб’єкта (електрона, атома) або макрооб’єкта з імпульсом p = mv нерозривно взаємопов’язаний з хвильовим процесом, довжина хвилі якого (так званої хвилі де Бройля)
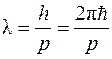 . (2.3)
. (2.3)
Цілий ряд дослідів повністю підтвердили хвильові властивості мікрооб’єктів на підставі наявності дифракційних та інтерференційних явищ як у випадку пучків електронів, атомів чи молекул газу, так і для по одиночних мікрооб’єктів.
У всіх зазначених дослідах довжина хвилі, притаманна різним мікрооб’єктам, узгоджувалася з довжиною хвилі де-Бройля (2.3).
Не дивно, що у випадку макрооб’єктів, які також мають корпускулярно-хвильову природу, експериментально переконатися у наявності хвильових властивостей практично неможливо. Внаслідок значної маси таких об’єктів довжина хвилі де-Бройля l лежить за межею досягнутої дотепер точності вимірювання відстаней (³ 10–18 м).
Так, для кулі масою m = 10–2 кг з швидкістю польоту v = 103 м/с маємо надзвичайно мале значення  згідно (2.3).
згідно (2.3).
Отже, у макрооб’єктів хвильові властивості менш помітні у порівнянні з корпускулярними. Згадайте, що кривизна гарматного ядра була очевидна в епоху середньовіччя, хоча інквізиція посилала на тортури та страту тих, хто вважав, що Земля має кулеподібну форму.
Зверніть увагу, що вирішальну роль при наведених оцінках відіграє не імпульс того чи іншого об’єкту, а стала Планка (квант найменшої дії) 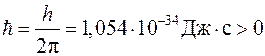 . При h ® 0 (класична фізика) маємо l = 0 для всіх об’єктів (мікро чи макро) при будь-яких значеннях їх імпульсів
. При h ® 0 (класична фізика) маємо l = 0 для всіх об’єктів (мікро чи макро) при будь-яких значеннях їх імпульсів 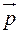 .
.
Взаємозв’язок поміж корпускулярними характеристиками (енергією W та імпульсом 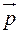 ) і хвильовими (частотою w та довжиною хвилі l) визначаються універсальними для всіх мікрооб’єктів співвідношеннями М. Планка – А. Ейнштейна:
) і хвильовими (частотою w та довжиною хвилі l) визначаються універсальними для всіх мікрооб’єктів співвідношеннями М. Планка – А. Ейнштейна:  ,
, 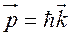 (2.4), де
(2.4), де  – хвильовий вектор, величина якого визначається як
– хвильовий вектор, величина якого визначається як 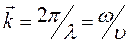 .
.
Проте взаємозв’язок поміж енергією W мікрооб’єктів та їх імпульсом 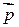 є індивідуальним, залежним від виду мікрооб’єкту.
є індивідуальним, залежним від виду мікрооб’єкту.
Індивідуальним, залежним від виду мікрооб’єкту є також і закон дисперсіїw( 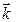 ), тобто залежність частоти w тієї чи іншої хвилі де-Бройля від її хвильового вектора
), тобто залежність частоти w тієї чи іншої хвилі де-Бройля від її хвильового вектора 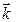 , який є характерною ознакою певної хвилі.
, який є характерною ознакою певної хвилі.
Розрізняються також групова и = vгр та фазова vф = v швидкість хвилі де-Бройля для мікрооб’єктів з малою масою m при швидкості їх руху v, бо фазова швидкість такої хвилі  , а групова швидкість хвилі де-Бройля
, а групова швидкість хвилі де-Бройля 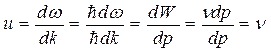 (2.5), тобто дорівнює швидкості руху v мікрооб’єкта, що свідчить про нерозривний взаємозв’язок хвиль де-Бройля з рухомими мікрочастинками.
(2.5), тобто дорівнює швидкості руху v мікрооб’єкта, що свідчить про нерозривний взаємозв’язок хвиль де-Бройля з рухомими мікрочастинками.
З’ясуємо фізичний зміст хвиль де-Бройля, зв’язаних з рухом певних мікрооб’єктів. Розглядаючи тиск світла на підставі хвильової чи корпускулярної його природи можна переконатися, що інтенсивність світлових хвиль J (квадрат її амплітуди J ~ Е2) в будь-якій точці простору пропорційна кількості N фотонів, які попадають саме в цю точку простору. Так само і інтенсивність хвилі де-Бройля в певній частині простору визначає кількість частинок (мікрооб’єктів), які потрапили в зазначену частину простору.
Саме ймовірнісну (статистичну) трактовку хвиль де-Бройля запропонував М. Борн, яка полягає в тому, що квадрат амплітуди хвилі де-Бройля в певній точці простору є мірою ймовірності знаходження мікрооб’єкту саме в цій точці.
Згідно формули (2.5) з будь-якою мікрочастинкою, що рухається з швидкістю v нерозривно зв’язана хвиля де-Бройля з груповою швидкістю и = v. Отже, частинка локалізована всередині хвильового пакету (цуга хвиль) шириною Dх (рис. 2.1), рухається вздовж осі х зшвидкістю 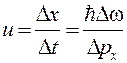 , звідки маємо
, звідки маємо 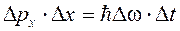 (2.6)
(2.6)
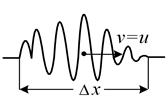 |
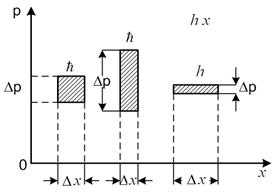
Рис. 2.1 Хвильовий пакет Рис. 2.2
Для будь-яких хвильових процесів виконуються співвідно-шення
 або
або 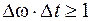 , (2.7)
, (2.7)
де Dw – інтервал частот монохроматичних хвиль, які утворюють хвильовий пакет (цуг); Dk – інтервал хвильових чисел ( 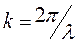 ) в хвильовому пакеті довжиною Dх.
) в хвильовому пакеті довжиною Dх.
Враховуючи (2.7) запишемо співвідношення (2.6) у вигляді
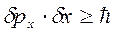 , (2.8)
, (2.8)
де рх – проекція імпульсу на вісь х.
Аналогічні співвідношення мають місце і у випадку руху мікрооб’єкта вздовж осей y або z
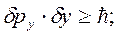
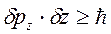 . (2.9)
. (2.9)
Стан квантового мікрооб’єкту згідно співвідношенню невизна-ченостей (2.8) не може бути заданий на площині (х, р) точкою, а задається прямокутником з площею  , величина якої визначається квантом дії, сталою М. Планка (рис. 2.2). При Dх ® 0 маємо Dрх ® µ і навпаки Dрх ® 0 при Dх ® µ. Отже, ці співвідношення забороняють рух мікрооб’єктів з суттєво вираженими хвильовими властивостями за певними траєкторіями. («орбітальний» рух електронів у атомі навколо ядра, тощо).
, величина якої визначається квантом дії, сталою М. Планка (рис. 2.2). При Dх ® 0 маємо Dрх ® µ і навпаки Dрх ® 0 при Dх ® µ. Отже, ці співвідношення забороняють рух мікрооб’єктів з суттєво вираженими хвильовими властивостями за певними траєкторіями. («орбітальний» рух електронів у атомі навколо ядра, тощо).
| |
| |
Обмежимося розглядом одномірного руху (вздовж осі х) нерелятивістського об’єкту в стаціонарному, тобто незалежному від часу, силовому полі.
В класичній механіці рівнянням такого руху є рівняння Ньютона (диференціальне рівняння другого порядку), причому стан класичного об’єкта в будь-який момент часу t однозначно задається рішеннями цього рівняння, тобто значеннями координати х(t) та імпульсу mv(t) за умови наявності їх значень (стану об’єкта) в початковий момент t = 0.
Для квантових мікрооб’єктів внаслідок їх корпускулярно-хвильового дуалізму (співвідношення невизначеностей) втрачає свій зміст класичне поняття стану мікрооб’єкта, поняття траєкторій, поняття сили, як функції класичного стану.
Експериментальні явища та відповідні гіпотези М.Планка та Луї-де-Бройля, накопичені на протязі першої чверті минулого століття, стали підґрунтям для створення зусиллями багатьох фізиків з різних країн всього за три роки (1925–1928 р.р) основ нерелятивістської квантової механіки.
В. Гейзенберг запропонував матричну теорію механіки мікрооб’єктів, надаючи перевагу дискретно-корпускулярному аспекту мікроявищ. В свою чергу Е. Шредінгер на підставі хвильових властивостей мікрооб’єктів(гіпотези Луї де Бройля) запропонував хвильове рівняння руху мікрооб’єктів.
Корпускулярно-хвильова двоєдиність природи мікрооб’єктів зумовлює те, що матрична механіка Гейзенберга та хвильова механіка Шредінгеравиявилися двома математичними різновидами нерелятивістської квантової механіки.
Нагадаємо, що основний закон електростатики [60] теж має дві математичні різновидності (закон Кулона та закон Гауса).
Визначаючи фізичний зміст хвиль де Бройля, саме М. Борн вперше довів імовірнісну (статистичну) інтерпретацію квантомеханічного опису стану не тільки систем мікрооб’єктів (пучків електронів, фотонів), але й поодиноких будь-яких мікрооб’єктів. Цим квантова механіка принципово відрізняється від класичної механіки, в якій статистичні імовірностні закони (розподіл Максвелла-Больцмана тощо) мали місце лише у випадку невпорядкованого руху значної кількості мікрооб’єктів N > 1025 (газ, тверде тіло). При цьому визначалися середні або найбільш ймовірні значення певної фізичної величини (швидкості, енергії тощо).
Імовірнісний характер мікросвіту, тобто статичні властивості як окремих мікрооб’єктів так і їх систем, зумовлюють визначення за допомогою квантової механіки ймовірностей достовірно не передбачених подій.
Саме хвильова функція Ψ(r, t) і є тією величиною в квантовій механіці Шредінгера, яка дозволяє знайти зазначені імовірності, а отже визначити середні значення випадкових фізичних величин (координати, швидкості, енергії тощо), тобто параметрів, які доступні експериментальному дослідженню. При цьому середнє значення визначається за допомогою квадрата модуля хвильової функції 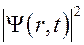 . Наприклад, середнє значення координати:
. Наприклад, середнє значення координати: 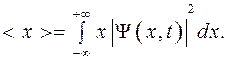
Фізичний зміст хвильової функції 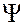 (r, t) полягає в тому, що квадрат її модуля визначає імовірність отримання інформації (область дії мікрооб’єкта, а не область його локалізації) в будь-який момент часу t в одиниці об’єму простору dv. Саме густина імовірності визначає форму та густину електронної оболонки атома (силует атома) в різних його станах (основному чи збудженому). Природно, що повна ймовірність виявлення мікрооб’єкту в усьому об’ємі V (електрон в атомі, нуклон в ядрі) дорівнює 1 (100 %)
(r, t) полягає в тому, що квадрат її модуля визначає імовірність отримання інформації (область дії мікрооб’єкта, а не область його локалізації) в будь-який момент часу t в одиниці об’єму простору dv. Саме густина імовірності визначає форму та густину електронної оболонки атома (силует атома) в різних його станах (основному чи збудженому). Природно, що повна ймовірність виявлення мікрооб’єкту в усьому об’ємі V (електрон в атомі, нуклон в ядрі) дорівнює 1 (100 %)
Така умова свідчить про достовірність події і має назву «умови нормування» в зв’язку з тим, що вона накладає певні обмеження на вибір коефіцієнтів для хвильової функції ψ.
В узагальненому випадку хвильова функція 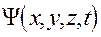 знаходиться як рішення нестаціонарного рівняння Шредінгера (диференціального рівняння другого порядку). Рівняння Шредінгера є фундаментальним рівнянням квантової механіки, яке подібно до рівняння Ньютона у класичній механіці є постулатом, тобто не може бути знайдене на підставі інших фізичних законів.
знаходиться як рішення нестаціонарного рівняння Шредінгера (диференціального рівняння другого порядку). Рівняння Шредінгера є фундаментальним рівнянням квантової механіки, яке подібно до рівняння Ньютона у класичній механіці є постулатом, тобто не може бути знайдене на підставі інших фізичних законів.
Більш уточнене, у порівнянні з (2.8) та (2.9) співвідношення поміж невизначеністю координат відповідних проекцій імпульсу може бути доведене (як на підставі хвильової механіки Шредінгера, так і на підставі матричної механіки Гейзенберга) у такому:
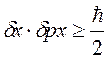 ;
; 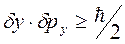 ;
;  (2.10)
(2.10)
Зверніть увагу, що співвідношення невизначеностей охоплює лише координати (х, у, z) та проекції імпульсу  , які співпадають за напрямком. На координати та складові імпульсів у взаємноперпендикулярних напрямках ці співвідношення не розповсюджуються. Це дозволяє знайти співвідношення невизначеностей поміж моментом імпульсу
, які співпадають за напрямком. На координати та складові імпульсів у взаємноперпендикулярних напрямках ці співвідношення не розповсюджуються. Це дозволяє знайти співвідношення невизначеностей поміж моментом імпульсу 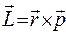 та кутом повороту
та кутом повороту 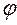 (азимутом) будь-якого точкового об’єкту.
(азимутом) будь-якого точкового об’єкту.
Оскільки зміщення об’єкту 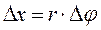 і співвідношення невизначеностей (2.10) не розповсюджується на плече r, тому його можна винести з під символа невизначеності координати і перенести у невизначеність проекції імпульсу;
і співвідношення невизначеностей (2.10) не розповсюджується на плече r, тому його можна винести з під символа невизначеності координати і перенести у невизначеність проекції імпульсу;
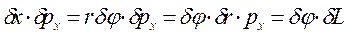
Отже, отримуємо співвідношення поміж невизначеністю проекцій моменту імпульсу 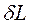 та невизначеність кута повороту
та невизначеність кута повороту 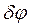 відносно відповідних осей у більш уточненому вигляді, а саме
відносно відповідних осей у більш уточненому вигляді, а саме

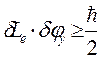 ;
; 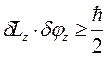 (2.11)
(2.11)
Співвідношення невизначеностей поміж координатами та відповідними проекціями імпульсу були вперше запропоновані в матричній механіці Гейзенберга і співпадають з такими ж співвідношеннями хвильової механіки Шредінгера.
Створюючи узагальнену математичну схему квантової механіки Гейзенберг спирався на принцип відповідності, який був для нього своєрідним дороговказом, орієнтиром пошуку математично строгого шляху для вирішення конкретних квантовомеханічних задач. Н.Бор вважав, що запропонований Гейзенбергом математичний апарат квантової механіки у вигляді матриці можна розглядати як „точну формуліровку тенденцій, закладених у принципі відповідності”.
На підставі цього принципу, представивши не лише класичну узагальнену координату q (аналог координати х), але й імпульс р у вигляді відповідних матриць
q = [ qmn.ехр.( i ωmn t) ], 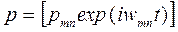 ,
,
саме М.Борн вперше довів перестановочне співвідношення в матричній квантовій механіці у вигляді
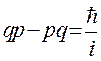 (2.12)
(2.12)
Саме такі некомутативні добутки qp та pq з не нульовою різницею, тобто перестановочні відношення на думку Гейзенберга та Йордана (творців матричної механіки) є аксіоматичним статутом в логічній структурі теорії.
На підставі перестановочного співвідношення та принципу відповідності були доведені не лише теорема про збереження енергії (умова частот Н. Бора при переході між сусідніми стаціонарними станами Wm та Wn), але й головне – універсальність сталої Планка  (кванта дії) завдяки об’єднанню двох ролей кванта дії h як оптичної константи в теорії спектрів та механічної в теорії атома.
(кванта дії) завдяки об’єднанню двох ролей кванта дії h як оптичної константи в теорії спектрів та механічної в теорії атома.
Наступним кроком удосконалення математичного апарату квантової механіки (у порівнянні з матрицями) є застосування теорії лінійних операторів, запропоноване М.Борном та Н.Вінером.
В теорії операторів, як і в теорії матриць, кожній динамічній змінній 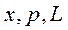 можна співставити певний оператор; а саме
можна співставити певний оператор; а саме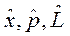 . Завдяки цьому досягається “можливість компромісу поміж новими некласичними поняттями з класичною механікою, можливість застосування схеми класичної механіки до мікросвіту, можливість використання в новій області поняття координат мікрооб’єкту, складових його імпульсу ...” [41].
. Завдяки цьому досягається “можливість компромісу поміж новими некласичними поняттями з класичною механікою, можливість застосування схеми класичної механіки до мікросвіту, можливість використання в новій області поняття координат мікрооб’єкту, складових його імпульсу ...” [41].
Цінність використання матриць та операторів полягає в тому, що вони надають можливість використання класичних понять, динамічних змінних (х, у, z, тощо) і визначають межі можливого застосування цих понять в квантовій фізиці мікросвіту.
Зокрема, такі статистичні уявлення класичної фізики, як ймовірності та статистичносереднє в зв’язку з корпускулярно-хвильовим дуалізмом квантових мікрооб’єктів виражаються за допомогою операторів та хвильових функцій 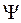 . При цьому фізичний зміст операторам, хвильовим функціям та їх співвідношенням надає узагальнене припущення про те, що будь-які значення операторів є середніми значеннями відповідних динамічних змінних. Отже, якщо хвильова функція не є власною функцією оператора, в такому випадку можна визначити експериментально і шляхом відповідних розрахунків лише середнє значення оператора.
. При цьому фізичний зміст операторам, хвильовим функціям та їх співвідношенням надає узагальнене припущення про те, що будь-які значення операторів є середніми значеннями відповідних динамічних змінних. Отже, якщо хвильова функція не є власною функцією оператора, в такому випадку можна визначити експериментально і шляхом відповідних розрахунків лише середнє значення оператора.
Окремим випадком цього припущення є те, що власні значення  оператора є цілком визначені значення динамічних змінних. З точки зору погляду на фізичні процеси це означає, що найбільш узагальненим випадком є реальні „стани невизначеності”, саме з яких у якості окремих випадків можуть виникати „стани визначеності”. Отже, вимірювання будь-якого квантово-механічного параметра, з яким зпівставляється оператор, зводиться до знаходження середнього або власного значення цього оператора.
оператора є цілком визначені значення динамічних змінних. З точки зору погляду на фізичні процеси це означає, що найбільш узагальненим випадком є реальні „стани невизначеності”, саме з яких у якості окремих випадків можуть виникати „стани визначеності”. Отже, вимірювання будь-якого квантово-механічного параметра, з яким зпівставляється оператор, зводиться до знаходження середнього або власного значення цього оператора.
Як і в теорії матриць, основою співвідношення невизначеностей Гейзенберга є перестановочні співвідношення поміж операторами відповідних фізичних величин(координат, проекцій, імпульсу, кутів повороту, проекцій моменту імпульсу тощо).
Зокрема для операторів координат та проекцій імпульсу ці перестановочні співвідношення мають вигляд
 (2.13)
(2.13) 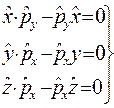 (2.14)
(2.14)
Якщо оператори комутативні (2.14), то динамічні параметри, представлені цими операторами, можуть бути одночасно виміряні з будь-якою точністю, тобто без невизначеності. Такими параметрами згідно (2.14) є координати та перпендикулярні до них складові (проекції) імпульсу.
Якщо оператори некомутативні (2.13), то вони не мають загальних власних функцій, а отже і власні значення цих операторів є несумісними. Це означає, що не існує такого стану квантової системи, при якому динамічні її параметри, представлені некомутативними операторами, могли б мати одночасно певні значення без відповідних невизначеностей. Це і є по суті визначення принципу невизначеності в операторній формі.
Отже, співвідношення невизначеностей може бути виведено при використанні будь-якої з математичних різновидностей квантово-механічної теорії,тобто по своїй суті є цілком логічним наслідком цієї теорії.
Взаємозв’язок принципу невизначеності та принципу відповідності полягає в тому, що суттєва зміна образу дослідження (об’єкта чи явища) неминуче зумовлювалася зміною не лише фізичних понять, уявлень або категорій (узагальнено-філософських понять), але й відповідною зміною математичних символів, понять, операцій.
Досить нагадати, що математичний апарат квантової механіки у вигляді матриць був запропонований В.Гейзенбергом при спробах з’ясування механізму переходу електрона в атомі з одного його енергичного стану в інший, де саме кожен з елементів матриці відповідає певному стану електрона і не потребує визначення траєкторії його переходу в інший стан, подібно до переходу будь-якої шахової фігури з початкового стану в кінцевий стан на шахівниці з 64 клітинок (станів). До речі В. Гейзенберг лише згодом дізнався про існування теорії матриць, розробленої математиками значно раніше, незалежно від уявлень квантової теорії. Більше того і у математичних понять, теорій, як і у природознавчих (фізичних, хімічних тощо), існують певні межі їх застосування, поза якими змінюється образ реальності.
Переконливим доказом цього є існування прикордонної межі (можливо досить прозорої), яка розділяє область застосування класичної фізики, де зміна місць співмножників не має значення (аb = bа або аb-вb=0), від області застосування квантової фізики з корпускулярно-хвильовою природою мікрооб’єктів, де добуток співмножників залежить від зміни їх місць, як у матричній теорії (2.12), так і в теорії лінійних операторів (2.13).
Тому цілком ймовірно, що на роль характеристичних параметрів в математичних апаратах класичної та квантової механік, що є однією з вимог принципу відповідності поміж цими теоріями, можуть претендувати відповідні пари невизначеностей 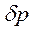 та
та 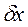 , або
, або  та
та 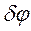 чи
чи 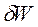 та
та 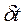 .
.
Методологічне значення принципу невизначеності полягає перш за все в тому, що всі без виключення поняття та фізичні параметри класичної фізики можуть бути використанні і в квантовій фізиці, але за обов’язкової умови припущення існуючої для кожного з цих понять характерної невизначеності, яка визначається відповідним співвідношенням невизначеностей. Зокрема, одна з теорем квантової механіки (теорема Еренфаста) доводить, що саме середні значення будь-яких фізичних параметрів, що описують квантові системи чи окремі квантові мікрооб’єкти, задовольняють рівняння та співвідношення класичної фізики.
Перейдемо до стислого аналізу суті та значення принципу невизначеності на підставі почергового розгляду наведених варіантів співвідношення невизначеностей поміж відповідними парами фізичних величин.
Відразу зазначимо, що не тільки методологічна суть, але й фізичний зміст співвідношень невизначеностей настільки не прості, що потребують кропіткого осмислення, співставлення та аналізу існуючих точок зору, пошуків переконливих аргументів, спростовуючи можливість не тільки реальних фізичних явищ, але й уявлень (мислених) експериментів, при яких нібито не мають місце зазначені співвідношення. Саме це свого часу стало предметом дискусій (на протязі багатьох років) поміж М.Бором та А.Ейнштейном.
При цьому висувалися гранично протилежні судження щодо принципу невизначеностей: від оцінки його як „видатного досягнення” до його повного несприйняття на підставі того, що вказаний принцип нібито зумовлює заборону пошуків більш глибоких чинників фізичних явищ мікросвіту. При цьому деякі з фізиків та філософів, за словами Джеммера „навіть вбачали в принципі Гейзенберга спосіб вирішення давнього філософського протиріччя поміж свободою волі та детермінізмом”, оскільки цей принцип нібито є своєрідним підтвердженням вчення Лукреція про те, що свобода волі людини можлива саме завдяки „незначним відхиленням первісних начал” [24].
В класичному світі принцип детермінації (взаємної однозначної зумовленості наслідків та чинників) дійсно дозволяв передбачати подальшу долю будь-якого фізичного об’єкта або системи за умови наявності повної інформації про них в попередній момент, тобто зокрема визначити траєкторію руху будь-яких класичних об’єктів (від параболічної у спортивних снарядів до еліптичної у планет Сонячної системи).
Принцип невизначеностей обмежує можливості отримання інформації щодо початкових умов руху мікрооб’єктів в квантових системах (електронів в атомі чи нуклонів в атомному ядрі) в зв’язку з їх корпускулярно-хвильовою двоєдиністю. При цьому саме хвильова компонента має ймовірнісну природу, яка й призводить до того, що через певний проміжок часу неминуче виявлять себе як невизначеність  в початковому положенні будь-якого квантового мікрооб’єкту, так і невизначеність
в початковому положенні будь-якого квантового мікрооб’єкту, так і невизначеність 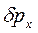 відповідної проекції його імпульсу (або швидкості
відповідної проекції його імпульсу (або швидкості 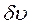 ).
).
Отже, такі поняття, як траєкторія, орбіта для квантових мікрооб’єктів перестають бути фізичною реальністю, тобто не можливо користуватися принципом детермінації в його класичному тлумаченні, а отже не можливо передбачити без відповідних невизначеностей як подальшу поведінку окремих квантових мікрооб’єктів, так і відповідно подальший (в часі) стан їх квантових систем (атомів чи ядер).
Таким чином, корпускулярно-хвильова двоєдиність квантових мікрооб’єктів та систем, виражена у відповідних співвідношеннях принципу невизначеностей, лише свідчить про відсутність адекватної моделі цих об’єктів в поняттях класичної науки, накопиченого життєвого досвіду і жодним чином не зумовлює будь-яку обмеженість „свободи волі” цих об’єктів, а тим самим і нібито обмеженість пізнання основних закономірностей квантового мікросвіту.
Навпаки, саме принцип невизначеностей у сукупності з іншими методологічними принципами посткласичної науки надали реальну можливість подальшого пізнання мікросвіту, можливість „…розуміти явища, які не можемо собі уявити”, як зазначав Л.Д.Ландау, характеризуючи досягнення сучасної фізики.
Співвідношення невизначеностей, як прояв об’єктивно існуючої корпускулярно-хвильової двоєдиності квантових мікрооб’єктів (найбільш суттєвої саме в мікросвіті), переконливо свідчать про об’єктивно існуючі обмеження при спробах чи можливостях одночасного описання цих об’єктів за допомогою класичних понять, а саме таких пар, як імпульс-координата або момент імпульсу та азимут (кут повороту). Ці принципово-об’єктивні обмеження хоча й впливають на точність визначення фізичних параметрів квантових мікрооб’єктів, проте ні в якій мірі не визначаються досягнутим рівнем точності вимірювальних приладів, тобто не можуть бути усунені завдяки удосконаленню вимірювальних засобів або методики експерименту.
Квантовий мікрооб’єкт, завдяки своїй корпускулярно-хвильовій природі, не допускає своєї одночасної локалізації в імпульсному та в координатному просторах. Об’єктивним законом природи є нерозривний взаємозв’язок поміж матерією та формами її існування (рухом та простором-часом), який саме в мікросвіті набуває нового за формою більш суттєвого значення. „Незалежності” певних характеристик рухомої матерії, як зазначає В.С.Готт, „прийшов кінець, тим більше, що особлива некласична сутність мікрооб’єктів потребувала нових понять для свого відображення” [21].
Саме принцип невизначеностей як наслідок корпускулярно-хвильової двоєдиності квантових мікрооб’єктів, в сконцентрованому вигляді визначає не лише головні особливості квантової теорії мікросвіту, але й спонукає до перегляду всієї теорії наукового пізнання [71]. В сучасній квантовій фізиці потребують корінного перегляду не лише поняття руху та детермінації подій, але й саме поняття спостереження в ідеалізованому класичному тлумаченні.
Для натурфілософів характерним було спостереження об’єктів чи явищ в природних умовах з подальшим формулюванням певних висновків. При цьому об’єкти та явища існували незалежно від спостереження, без будь-якого втручання з боку спостерігача. В класичній науці (починаючи з дослідів Г.Галілея у ХVІ сторіччі) об’єкти чи явища стають предметом спостереження лише за умови застосування певного способу вимірювання їх основних властивостей за допомогою відповідних еталонів довжини, часу тощо.
Отож, спостереження нерозривно пов’язане з вимірюванням, тобто з взаємодією експериментального обладнання з об’єктом дослідження, яке неминуче супроводжується порушенням первісного стану не лише цього об’єкту, але й вимірювальних приладів. Класичне природознавство ґрунтується на припущенні, що спотворену втручанням приладу інформацію відносно об’єкту дослідження можна певним чином врахувати і тим самим за результатами експериментального вимірювання отримувати висновки про істинний, первісний стан цього об’єкту чи явищ.
В.Гейзенберг був першим, хто не лише зрозумів, що в посткласичній науці мікросвіту, зокрема, в квантовій фізиці, поняття „явища” та „спостереження” нерозривно взаємозв’язані, але й визначив цей взаємозв’язок у вигляді співвідношень невизначеностей. При цьому спостереження квантових мікрооб’єктів чи квантових систем (атомів, ядер тощо) є по суті теж досить складним явищем, оскільки будь-яке вимірювання порушує первісний стан об’єкта.
Таким чином, принцип невизначеностей, як складова частина методологічного підґрунтя квантової механіки, дозволяє значно глибше у порівнянні з уявленнями класичної механіки розкрити сутність руху, передбачаючи, що будь-які фізичні явища, які обмежують розташування квантового мікрооб’єкту в просторі (координати х, у, z або 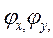
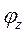 ), одночасно призводять до змін його імпульсу
), одночасно призводять до змін його імпульсу 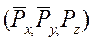 або моменту імпульсу
або моменту імпульсу 
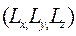 . Отже, в квантовій механіці „будь-яке просторове обмеження руху неминуче пов’язане з підвищенням інтенсивності руху і тому ніяка взаємодія не може припинити рух частинки” [21].
. Отже, в квантовій механіці „будь-яке просторове обмеження руху неминуче пов’язане з підвищенням інтенсивності руху і тому ніяка взаємодія не може припинити рух частинки” [21].
Наприклад, визначити локалізацію, просторове розташування електрона як квантового мікрооб’єкту можливо за допомогою кванта випромінювання (фотона видимого світла з довжиною хвилі  м або ж гамма-кванта з довжиною хвилі
м або ж гамма-кванта з довжиною хвилі 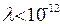 м). При такій взаємодії або зіткненні квантів випромінювання з електроном (явище Комптона) відбувається як зміна їх імпульсів, так і зміна початкового просторового розташування електрона, тобто порушується первісний стан електрона.
м). При такій взаємодії або зіткненні квантів випромінювання з електроном (явище Комптона) відбувається як зміна їх імпульсів, так і зміна початкового просторового розташування електрона, тобто порушується первісний стан електрона.
Квант випромінювання з імпульсом 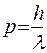 при розсіюванні на електроні надає останньому додаткового імпульсу
при розсіюванні на електроні надає останньому додаткового імпульсу 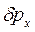 , перпендикулярного до осі мікроскопа, яке визначається у вигляді
, перпендикулярного до осі мікроскопа, яке визначається у вигляді
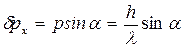 (2.15)
(2.15)
Нагадаємо, що розподільча здатність будь-якого мікроскопу, тобто найменші розміри об’єкту спостереження, визначаються згідно дифракційній теорії теж в залежності від довжини хвилі 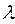 та кута
та кута 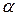 у вигляді
у вигляді
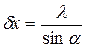 . (2.16)
. (2.16)
Якщо в оптичній мікроскопії можна розглядати мікрооб’єкти з розмірами 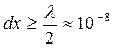 м, то розподільча здатність електронного мікроскопа визначається довжиною хвилі де Бройля електрона, яка при прискорюючий напрузі
м, то розподільча здатність електронного мікроскопа визначається довжиною хвилі де Бройля електрона, яка при прискорюючий напрузі 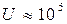 В становить
В становить 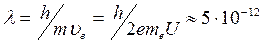 м.
м.
Наведений спрощений аналіз подібної взаємодії квантових мікрооб’єктів призводить до підтвердження об’єктивності існування принципу співвідношення у наближеній формі (2.8) як добутку (2.15) та (2.16).
Таким чином, квантові закони взаємодії, руху, не відкидають відповідні класичні закони, але лише визначають певну кількісну межу можливості застосування останніх. Зокрема, одночасне використання таких пар класичних понять як імпульс-координата; момент імпульсу-кут повороту (азимут); енергія-час для описання фізичних явищ в квантових системах мікрооб’єктів можливе лише за умови введення в їх інтерпретацію квантової поправки. Саме такою поправкою, своєрідним обмеженням і є співвідношення невизначеностей як прояв принципу невизначеностей. Ця нерозривна єдність якісно нової природи квантових мікрооб’єктів та гносеологічної необхідності використання(правда, досить своєрідно та обмежено) мови класичної механіки і виражає принцип невизначеностей, який В.О.Фок назвав „принципом обмеженого застосування класичних моделей” [103].
Підтвердимо це на прикладі фізичних явищ. Розглянемо рух електрона 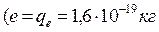 та
та 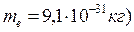 у вакуумній електронно-променевій трубці (кінескоп телевізора, монітора тощо). Величина швидкості та імпульсу електрона визначаються величиною прискорюючої напруги, яка становить як правило
у вакуумній електронно-променевій трубці (кінескоп телевізора, монітора тощо). Величина швидкості та імпульсу електрона визначаються величиною прискорюючої напруги, яка становить як правило 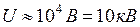 . За таких умов швидкість електрона становить
. За таких умов швидкість електрона становить  , а величина імпульсу відповідно
, а величина імпульсу відповідно 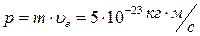 . Зовсім не важко досягти точність вимірювання напруги U до декількох мікровольт, що забезпечить точність вимірювання швидкості до 0,01%, тобто відповідна невизначеність швидкості електрона
. Зовсім не важко досягти точність вимірювання напруги U до декількох мікровольт, що забезпечить точність вимірювання швидкості до 0,01%, тобто відповідна невизначеність швидкості електрона 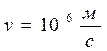 становить
становить 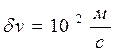 .
.
На підставі уточненого співвідношення невизначеностей (2.10) оцінюємо невизначеність координати 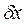 електрона
електрона


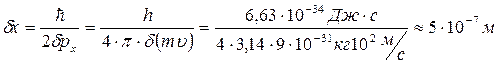
Порівнюючи цю величину з геометричними розмірами трубки 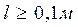 приходимо до висновку, що квантові невизначеності надзвичайно малі, тобто поняття траєкторії руху має свій сенс і сам рух електронів в кінескопі з високою точністю описується відповідними рівняннями класичної механіки.
приходимо до висновку, що квантові невизначеності надзвичайно малі, тобто поняття траєкторії руху має свій сенс і сам рух електронів в кінескопі з високою точністю описується відповідними рівняннями класичної механіки.
Разом з тим нерелятивістський електрон, що рухається у атомі з діаметром  з такою ж швидкістю
з такою ж швидкістю 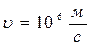 і має наведену невизначеність координати
і має наведену невизначеність координати 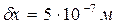 ніяк не можна вважати рухом за певними траєкторіями, „орбітами”. Отже рух електрона в атомі описується виключно законами квантової механіки.
ніяк не можна вважати рухом за певними траєкторіями, „орбітами”. Отже рух електрона в атомі описується виключно законами квантової механіки.
Пропонуємо самостійно довести за допомогою співвідношень невизначеностей (2.10), що нуклони (нейтрони та протони) з масою 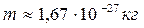 можуть міститися у атомному ядрі з діаметром
можуть міститися у атомному ядрі з діаметром 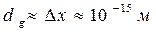 , а електрони не можуть входити до складу ядра, перебуваючи в електронній оболонці атома діаметром
, а електрони не можуть входити до складу ядра, перебуваючи в електронній оболонці атома діаметром  .
.
Використовуючи співвідношення невизначеностей координата-імпульс (2.10), можливо не тільки оцінити лінійні розміри одноелектронного атома водню, тобто його радіус ( 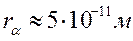 ), але й енергію зв’язку або іонізаційний потенціал такого атома. Поряд з цим саме зазначене співвідношення невизначеностей дозволяє пояснити існуючу стабільність будь-якого атома. Падіння електронна на ядро внаслідок втрати енергії неможливо, бо при такому наближенні невизначеність в значеннях координат
), але й енергію зв’язку або іонізаційний потенціал такого атома. Поряд з цим саме зазначене співвідношення невизначеностей дозволяє пояснити існуючу стабільність будь-якого атома. Падіння електронна на ядро внаслідок втрати енергії неможливо, бо при такому наближенні невизначеність в значеннях координат 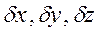 такого електрона будуть стрімко зменшуватися
такого електрона будуть стрімко зменшуватися 
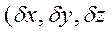
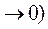 . Але при цьому згідно (2.10) буде неминуче зростати невизначеність відповідних компонент імпульсу електрона (
. Але при цьому згідно (2.10) буде неминуче зростати невизначеність відповідних компонент імпульсу електрона (  , яка зумовлює і відповідне зростання за величиною енергії електрона, тобто віддалення такого електрона від ядра.
, яка зумовлює і відповідне зростання за величиною енергії електрона, тобто віддалення такого електрона від ядра.
На підставі принципу невизначеностей, тобто їх відповідних співвідношень, знаходять пояснення і такі фізичні явища мікросвіту, як існування нульових коливань квантового осцилятора; радіоактивний 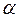 -розпад або невимушений спонтанний розпад важких ядер з випромінюванням
-розпад або невимушений спонтанний розпад важких ядер з випромінюванням 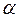 -частинок (ядер
-частинок (ядер 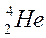 ); холодна автоелектронна емісія. Останні два випадки є проявами тунельного ефекту, тобто можливості подолання квантовим мікрооб’єктом (електроном, альфа-частиною тощо) потенціального енергетичного бар’єру кінцевої висоти.
); холодна автоелектронна емісія. Останні два випадки є проявами тунельного ефекту, тобто можливості подолання квантовим мікрооб’єктом (електроном, альфа-частиною тощо) потенціального енергетичного бар’єру кінцевої висоти.
Не менш важливим є співвідношення невизначеностей енергії 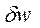 квантового мікрооб’єкта або квантової системи (атома, ядра) та часу
квантового мікрооб’єкта або квантової системи (атома, ядра) та часу 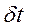 його перебування в певному енергетичному стані, яке з врахуванням (2.4) та (2.7) може бути представлене як у наближеному варіанті
його перебування в певному енергетичному стані, яке з врахуванням (2.4) та (2.7) може бути представлене як у наближеному варіанті
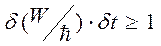 або
або 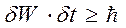 , (2.17)
, (2.17)
так і в більш уточненому варіанті
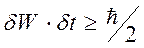 (2.18)
(2.18)
Слушно нагадати, що будь-яка відповідна пара співвідношень невизначеностей (2.10), (2.11) чи (2.18) є лише кількісними співвідношеннями, які відображають методологічний принцип невизначеностей для обраного окремого випадку. При цьому будь-яке з зазначених співвідношень „не є висновком з аналізу процесу вимірювання”, що розглядається в класичних поняттях” [15].
Отже, принцип невизначеностей віддзеркалює якісно нові властивості мікросвіту, проявом яких є явища квантової фізики.
Наведемо більш детальний аналіз суті змісту співвідношення невизначеностей для енергії та часу, обмежившись наближеним їх варіантом (2.17). При визначені значення енергії W будь-якої квантової системи (атома, ядра тощо), яка перебуває в стаціонарному стані внаслідок впливу вимірювальної апаратури, тобто взаємодії вимірювального приладу з квантовою системою на протязі часового інтервалу 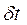 , невизначеність результату вимірювання
, невизначеність результату вимірювання 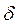 W обмежена величиною
W обмежена величиною 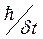 .
.
Якщо ж будь-яка замкнена система квантова система (атом, ядро) знаходиться в нестаціонарному збудженому стані на протязі характерного часового інтервалу 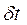 (середнього часу життя збудженого атому), тоді енергія такого нестабільного стану згідно співвідношенню (2.32) має невизначеність
(середнього часу життя збудженого атому), тоді енергія такого нестабільного стану згідно співвідношенню (2.32) має невизначеність
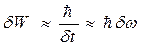 (2.19)
(2.19)
Отже, всі збуджені енергетичні рівні дискретного спектру енергій, розташовані вище основного рівня, мають кінцеву ширину 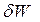 . Середнє значення часу життя переважної більшості збуджених атомів становить
. Середнє значення часу життя переважної більшості збуджених атомів становить 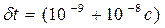 , що дає кінцеву ширину збудженого стану
, що дає кінцеву ширину збудженого стану 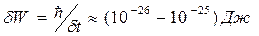 . Нагадаємо про існування так званих метастабільних станів з часом життя
. Нагадаємо про існування так званих метастабільних станів з часом життя  . Для них ширина
. Для них ширина 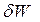 енергетичного рівня значно менша.
енергетичного рівня значно менша.
Експериментальним підтвердженням наведеного є спектральна ширина 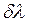 або
або 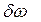 будь-якої лінії випромінювання в дискретному спектрі випромінювання атома, значний внесок в яку належить „природній” ширині
будь-якої лінії випромінювання в дискретному спектрі випромінювання атома, значний внесок в яку належить „природній” ширині 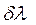 або
або 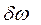 , величина якого визнається співвідношенням невизначеностей (2.19) за умови „ідеального” експерименту, тобто при повній відсутності зовнішнього впливу на квантову систему. Отже, енергія будь-якого збудженого стану атома окрім основного, або значення енергії рівнів дискретного енергетичного спектру атома за винятком найнижчого (n = 1) може бути відома з невизначеністю
, величина якого визнається співвідношенням невизначеностей (2.19) за умови „ідеального” експерименту, тобто при повній відсутності зовнішнього впливу на квантову систему. Отже, енергія будь-якого збудженого стану атома окрім основного, або значення енергії рівнів дискретного енергетичного спектру атома за винятком найнижчого (n = 1) може бути відома з невизначеністю  , де
, де 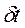 – середній час життя збудженого стану, тобто проміжок часу протягом якого буде випромінений квант з частотою
– середній час життя збудженого стану, тобто проміжок часу протягом якого буде випромінений квант з частотою  , де
, де 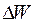 – різниця енергій поміж сусідніми рівнями, яка значно перевищує невизначеність
– різниця енергій поміж сусідніми рівнями, яка значно перевищує невизначеність 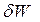 будь-якого з енергетичних рівнів
будь-якого з енергетичних рівнів  .
.
Невизначеністю енергії основного стану (найнижчого рівня в енергетичному спектрі при n = 1) можна знехтувати, бо саме в цьому стані атом чи ядро можуть перебувати на протязі будь-якого проміжку часу 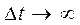 при відсутності зовнішнього впливу.
при відсутності зовнішнього впливу.
Співвідношенням невизначеностей енергія-час(2.19) пояснюється і досить широкий спектр енергій 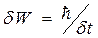 альфа-частинок при радіоактивному розпаді важких ядер з часом життя
альфа-частинок при радіоактивному розпаді важких ядер з часом життя 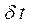 таких ядер збудженому стані.
таких ядер збудженому стані.
Ще більш значний за величиною енергетичний спектр 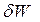 (значення енергії в широкому діапазоні) мають „елементарні частинки”. Зокрема для нового типу елементарних частинок (відомих під назвою резонанси) час життя, тобто інтервал часу поміж миттю їх народження та миттю їх анігіляції), становить
(значення енергії в широкому діапазоні) мають „елементарні частинки”. Зокрема для нового типу елементарних частинок (відомих під назвою резонанси) час життя, тобто інтервал часу поміж миттю їх народження та миттю їх анігіляції), становить 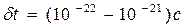 . Тому невизначеність енергії таких елементарних частинок досить суттєва
. Тому невизначеність енергії таких елементарних частинок досить суттєва 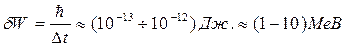 і може відігравати визначальну роль в реакціях по взаємоперетворенню елементарних частинок.
і може відігравати визначальну роль в реакціях по взаємоперетворенню елементарних частинок.
Слід підкреслити, що співвідношення невизначеностей в будь-якому з розглянутих варіантів є фундаментальними закономірностями ймовірнісного квантового мікросвіту з корпускулярно-хвильового двоєдиністю його квантових мікрооб’єктів, а тому ні в якому разі не зумовлений точністю вимірювальних приладів або похибками процесу вимірювання.
Принцип невизначеностей проголошує принципову неможливість одночасного отримання інформації про координати та проекції імпульсу або про значення енергії на протязі певного часу для будь-якого квантового мікрооб’єкту, позбавленої відповідних невизначеностей. Тому цей принцип є не лише подальшим посиленням тенденцій, закладених у принципі відповідності, але й проявом в певній мірі такого методологічного принципу як принцип неможливості, який прогнозує і стверджує принципову неможливість, заборону певних фізичних явищ ( 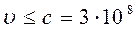 м/с,
м/с,  , к.к.
, к.к. 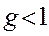 ) .
) .
Таким чином, принцип невизначеностей як один з основних принципів сучасної науки має безсумнівно методологічне значення не лише у з’ясуванні суті явищ атомної фізики, ядерної фізики та фізики елементарних частинок, але й в суттєвому перегляді структури теорії наукового пізнання.
Саме принцип невизначеності Гейзенберга став своєрідним підгрунттям для запропонованого Н.Бором методологічного принципу сучасного природознавства і названого ним як принцип доповнювальності.
Читайте також:
- Аграрна політика як складова економічної політики держави. Сутність і принципи аграрної політики
- Адекватна реалізація принципів міжнародної економіки можлива лише в стабільному політичному середовищі.
- Адміністративна відповідальність: поняття, мета, функції, принципи та ознаки.
- Адміністративні методи - це сукупність прийомів, впливів, заснованих на використанні об'єктивних організаційних відносин між людьми та загальноорганізаційних принципів управління.
- Алкмеон. Принцип нервізма. Нейропсіхізм. Принцип подібності
- Аналогія права - вирішення справи або окремого юридичного питання на основі принципів права, загальних засад і значення законодавства.
- Антикорупційні принципи
- Антикорупційні принципи
- Антикорупційні принципи
- Антикорупційні принципи
- Антропологічний принцип філософії Л. Фейербаха
- Архитектура ЭВМ, построенная на принципах фон Неймана
| <== попередня сторінка | | | наступна сторінка ==> |
| Принцип відповідності | | | Принцип доповнювальності |
|
Не знайшли потрібну інформацію? Скористайтесь пошуком google: |
© studopedia.com.ua При використанні або копіюванні матеріалів пряме посилання на сайт обов'язкове. |