Новини освіти і науки:

G+

Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция

Принципи інваріантності, симетрії

Серед сукупності методологічних принципів сучасного природознавства надзвичайно суттєву роль відіграють принципи симетрії, інваріантності, які виявляють структуру фізичних теорій та взаємозв’язок притаманних цим теоріям законів, тобто безпосередньо спрямовані на вирішення головної проблеми методології фізики, яка полягає в аналізі способів побудови теорій відповідним дослідженням структурної побудови фізичних теорій.

В фізико-математичному аспекті симетріярозглядається як наявністьв фізичних об’єктах, процесах чи явищах фізичної характеристики або сукупності характеристик, які залишаються незмінними, інваріантними при різних перетвореннях[6]. Тому розрізняють різні види симетрії (просторову, часову, зарядову, калібрувальну та інші), які і визначають в першу чергу специфіку тієї чи іншої фізичної теорії.

В більш розширеному варіанті ідея симетрії передбачає не лише інваріантність, незмінність, але й незалежність деякої сукупності параметрів, властивостей, типів взаємодій відносно тих чи інших фізичних умов та певних груп перетворень.

Якщо розглядати симетрію як критерій подібності, схожості або тотожності, то цілком припустимо вважати, що принципи симетрії, інваріантності є також ефективними методологічними засобами уніфікації, які надають змогу визначити, знайти подібне, тотожне в різноманітному і на цій підставі відшукати модель чи узагальнену теорію, об’єднуючу сукупність об’єктів чи явищ.

У повсякденній практиці симетрію найчастіше розуміють у її звуженому варіанті, тобто, як просторову симетрію, одним із прикладів якої є симетрія кристалів. Зовнішньою ознакою такої симетрії є наявність однакових за розміром, закономірно розташованих структурних елементів системи з регулярних їх повторенням при певних просторових перетвореннях.

Автор глави „Принцип симетрії” [58] В.В. Визгін зазначає, що в зв'язку з наявністю множини типів симетрій „…в сучасній фізиці здебільшого йде мова не про принцип, а про принципи симетрії”.

Принципи симетрії органічно пов’язані, більш того, вони по суті співпадають з принципами відносності та інваріантності, фактично це – різні назви одних і тих же принципів. По меншій мірі таким є дотеперішній стан. Отже, „симетрія”, „відносність”, „інваріантність”та „незмінність” є нібито проекціями поняття, яке ми називаємо „симетрією”.

Проте, має місце протилежний підхід, який ґрунтується на некоректності ототожнювання понять інваріантності та симетрії визначення. „Різниця поміж симетрією та інваріантністю полягає в тому, що інваріантність законів, поряд з симетрією, визначає і ступінь узагальненості цих законів, тобто межі їх застосування”. Інваріантність законів природи – наслідок тих суттєвих симетрій, які – правда, не в повній мірі – входять у їх зміст.

Визнаючи те, що існують переконливі підстави для ототожнювання симетрії та інваріантності, що по відношенню до певних умов дії фізичних законів поняття симетрії та інваріантності співпадають, автор книги [21] наполягає на тому, що „…жодна з форм симетрії повністю не обумовлює ступінь узагальненості законів, межі їх дії, тобто їх інваріантність”. Інваріантність узагальнених законів може бути пов’язана з симетріями різних груп перетворень, „…з різними видами симетрій. Симетрія однозначно інваріантність законів не визначає”.

Враховуючи і виділяючи найбільш суттєве і спільне у цих двох розглянутих підходах, ми вважаємо найбільш доцільним вживання назви „принципи інваріантності, симетрії”. Саме така назва підкреслює визначальну роль інваріантності, незмінності фізичних параметрів(енергія, імпульс, момент імпульсу, електричний заряд, баріонні, лептонні заряди та інших), або фізичних законів, відносно різних видів симетрії, певних операцій (перетворень), яких зазнає обрана фізична система. Цим підкреслюється, що фізичні закони, якими визначається будь-яка фізична теорія, повинні спиратися виключно на динамічні зміні та на абсолютні, інваріантні фізичні параметри, які визначаються експериментально.

При цьому інваріантність певного фізичного динамічного закону зумовлюється типом симетрії, тобто в математичному відношенні з групою перетворень деяких характерних змінних тієї чи іншої фізичної теорії.

Існує глибокий внутрішній зв’язок поміж трьома рівнями опису (трьома класами фізичних закономірностей): рівнем явищ (подій), законів та принципів симетрії. Саме закони фізики (регулярності чи ідентичності в явищах природознавства) за наявності початкових умов є кореляціями поміж явищами (подіями), розкриваючи їх взаємозв’язок та структуру. В свою чергу, ті чи інші принципи інваріантності, симетрії „…дозволяють відкривати нові закони і в цьому сенсі є кореляціями поміж законами. Якщо закони керують подіями, то принципи симетрії керують законами, …виявляють структуру фізичних теорій та зв’язок притаманних їм законів. Саме ця ознака принципів симетрії виводить їх на методологічний рівень…” [58].

Як вже зазначалося, принципи симетрії, а точніше, конкретні симетрії(перетворення сукупності фізичних параметрів) мають емпіричний статут. Про це свідчить те, що фізичними чинниками симетрії можуть бути характер та спрямованість сил взаємодії між мікрооб’єктами фізичної макросистеми, дискретність розподілу речовини, спрямування фізичної макросистеми до рівноважного стану з мінімальним значенням внутрішньої енергії. При цьому тип (вид) симетрії може залежати від способу описування фізичних об’єктів, явищ або їх параметрів (скалярного, векторного чи тензорного).

Нагадаємо, що для сили характерна симетрія полярного вектора, для пари сили (обертального моменту), моменту імпульса, магнітного поля кільцевого струму – симетрія аксіального вектора. В той же час гальваномагнітному ефекту Холла властива симетрія полярного тензору другого рангу, а п’єзоелектричному ефекту – тензора третього рангу.

Подібний перелік фізичних явищ та відповідних типів симетрій можна продовжувати. Тому виникає потреба в спробах класифікації існуючого дотепер „…надзвичайно широкого спектру різноманітних принципів симетрії, які відрізняються одним від одного рівнем узагальненості, точністю, різноманіттям, на які діють відповідні групи, характером зміни параметрів цих груп (безперервний чи дискретний, кінцевопараметричні або нескінченні групи і т. ін.), ступенем фізичної обґрунтованості, мірою наочності і т.п.” [58]. Саме цим і пояснюються відсутність єдиної загальновизнаної класифікації принципів симетрії.

В найбільш узагальненому варіанті існуючі принципи симетрії розподіляються на два основні види: зовнішні (просторово-часові, геометричні) та внутрішні (динамічні).

До першої групи відносяться принципи симетрії (відносності), які можуть бути сформульовані в термінах подій і відображають симетрію (псевдо-евклідову геометрію чотиривимірного простору-часу) відносно таких безперервних його перетворень:

а) перенесення (зсув) системи відліку (СВ) як цілого в просторі, при якому симетрія фізичних законів означає однорідність простору(еквівалентність всіх його точок);

б) поворот СВяк цілого в просторі, при якому симетрія фізичних законів відносно такого перетворення означає ізотропність простору (еквівалентність всіх його напрямків);

в) зміна початку відліку часу(зсув за часом), при якому симетрія фізичних законів відносно такого перетворення означає їх незмінність з часом.

Нагадаємо, що існування єдиного чотиривимірного простору-часу є головним наслідком спеціальної теорії відносності. Інваріантним в такому просторі-часі є просторово-часовий інтервал S_1,2 поміж подіями.

До другої групи внутрішніх принципів симетрії слід віднести сукупність принципів симетрії негеометричного характеру, тобто динамічних принципів, пов’язаних з певними існуючими чотирма типами фундаментальних взаємодій.

До внутрішніх (динамічних) симетрій сучасної квантової фізики та фізики елементарних частинок належать такі типи симетрії:

а) ізотопічна інваріантність сильної взаємодії і унітарна SU(3) симетрія, яка, зокрема, визначає зарядову незалежність ядерних сил;

б) „кольорова” симетрія, тобто, симетричність сильної взаємодії відносно перетворення трьох „кольорів” кварків (особливих квантових чисел, що визначають три різні стани кварка), яка й забезпечує утримання кварків в адронах;

в) симетрія між кварками та лептонами, яка згідно експериментальним дослідженням, забезпечує електрослабку їх взаємодію і є одним з можливих варіантів пошуку єдиної теорії всіх фундаментальних взаємодій, найсуттєвішої методологічної проблеми сучасної фізики;

г) суперсиметрія(симетрія Фермі-Бозе), яка пов’язує поля квантів з навпіл цілим спіном (ферміонів) з полями квантів цілим спіном (бозонів), зумовлюючи зокрема інваріантність ядерних силпри заміні нейтрона протоном або π⁺ - мезона відповідно π^- - мезоном, перевірена експериментально;

д) калібрувальна симетрія, пов’язана з неспостережуванністю хвильових функцій квантових систем і наслідком якої є інваріантністьпевних фізичних параметрів з узагальненою назвою „заряд” (електричний заряд, гіперзаряд, лептонний L та баріонний B заряди, ізотонічний спін J, колір тощо), які одночасно є і джерелами полів, що переносять взаємодію поміж елементарними частинками.

Переважна більшість динамічних симетрій (мікросиметрій) має наближений характер, і за деяких умовах спостерігаються порушення певних видів внутрішніх симетрій.

Надзвичайно важливою є залежність типу внутрішньої симетрії від відносної інтенсивності чотирьох видів взаємодії, що представлена в таблиці 3 додатку. Чим сильніша за інтенсивністю взаємодія, тим вище відповідна йому динамічна (внутрішня) мікросиметрія. Так, при сильній взаємодії інваріантнимиє всі внутрішні квантові числа (q, B, S, J, P), тобто спостерігається збереження цих характеристик.

При електромагнітній взаємодії інваріантнимизалишаються q,B та S, при слабкій взаємодії – лише q та B (табл. 3 додатку), проте при зростанні енергії взаємодіючих елементарних частинок зазначена залежність дещо послаблюється.

Особливе місце в наведеній класифікації симетрій займає симетрія, пов’язана з загальною теорією відносності (ЗТВ) – теорію неевклідового викривленого простору-часу, яка здається на перший погляд суто геометричною. Однак суть ЗТВ полягає в залежності геометричних елементів (метрики) від маси взаємодіючих об’єктів, яка має динамічний характер. Це дає певні підстави віднести таку симетрію до другої групи, тобто до динамічних симетрій.

Поза запропонованим розподілом симетрій на дві групи залишилися симетрії, пов’язані з дискретним(перервним) перетворенням простору-часу, або так звані дискретні види симетрій, які відіграють визначальну роль в фізиці елементарних частинок (просторової інверсії Р, зміни плину часу Т, зарядового спряження С), які охоплюються СРТ – теоремою, основною теоремою квантової теорії поля. Ця теорема відіграє вирішальну роль в пошуках єдиної теорії фундаментальних взаємодій, адже саме вона передбачає релятивістську інваріантністьта локальність цих взаємодій.

За останній час набули широкого визнання суперсиметрії, які об’єднують безперервні та перервні (дискретні) перетворення, виявляючи миті ототожнення фізичного поля та речовини як існуючих видів матерії.

Переважна більшість наведених симетрій, (безпосередньо пов’язаних з взаємодіями елементарних частинок), мають суттєве значення для вирішення існуючих методологічних проблем сучасної фізики, зокрема, класифікації елементарних частинок та створення єдиної теорії взаємодій поміж ними.

Саме принципи симетрії, інваріантності, як засоби уніфікації, своєрідного спрощення сукупності елементарних частинок, стали підставою для поєднання адронів, (посередників сильної взаємодії) у мультиплетну групу та подальшого об’єднання таких мультиплетів у супермультиплети.

Поряд з цим, принципи симетрії стали основою для створення одного з варіантів об’єднання електромагнітної та слабкою взаємодії, однієї з важливих стадій розробки моделі об’єднання всіх існуючих видів взаємодій.

Поки-що поза нашою увагою залишилися симетрії, які набули широкого розповсюдження з появою квантової механіки і стали визначальними саме для квантових систем (атомів, ядер). В першу чергу це – перестановочнасиметрія, тобто симетрія відносно перестановка однакових квантових мікрооб’єктів, з яких складається певна квантова система.

Хвильова функція (Ψ – функція) такої системи симетрична (не змінює свій знак) лише за умови перестановки будь-якої пари бозонів),тобто тотожних квантових мікрооб’єктів з нульовим або цілочисленним спіном. У випадку перестановки ферміонів(електронів, нуклонів), тобто тотожних мікрооб’єктів з навпілцілим спіном, хвильова функція стає антисиметричною, тобто змінює свій знак. З розглянутим типом симетрії хвильової функції пов’язані відповідні квантові статистики для системи квантових мікрооб’єктів: ферміони підлягають статистиці Фермі-Дірака, бозони-статистиці Боза-Ейнштейна. На підставі цих статистик створена квантова теорія електропровідності, зонна теорія твердих тіл.

З явною або прихованою симетріями пов’язане і виродження енергетичних рівнів квантових систем (багато-електронних атомів, ядер). При цьому наявність в квантовій системі таких станів (вироджених за енергіями) свідчить про існування симетрії взаємодії невідомого типу.

Навіть наведена стисла характеристика різних симетрій досить переконливо свідчить про те, що розглянутий розподіл існуючих типів симетрій на два види (геометричний та динамічний) є досить умовним, тобто, не є універсальним (всеузагальненим).

По-перше, це значна за своєю кількістю сукупність існуючихнині різноманітних типів симетрій, а отже, і відповідних їх методологічних принципів симетрії, які відрізняються один від одного рівнем узагальненості, точності та різноманітності, ступенем фізичної обґрунтованості.

По друге – емпіричний статут конкретних типів симетрій, завдяки якому відкриття нових фізичних явищ та законів може привести до порушення принципів симетрії, які видаються іноді непорушними, і до відкриття нових зовсім не очевидних принципів симетрії. „…зокрема відкриття великої кількості внутрішніх симетрій в фізиці елементарних частинок на протязі останніх десятиріч” [58].

По третє, існуючий взаємозв’язок поміж самими двома видами: сукупністю геометричних симетрій та сукупністю динамічних симетрій. Цей взаємозв’язок зовнішньої симетрії (властивості простору-часу) та внутрішньої симетрії (властивостей взаємодій) обумовлений внутрішнім нерозривним взаємозв’язком поміж основними атрибутами матерії: простором, часом, рухом і охопленою ним взаємодією.

Таким чином, будь-яка з існуючих форм (типів, видів) симетрій, яка визначає процес існування та становлення тотожних моментів в певних умовах і в певних відношеннях поміж різними і протилежними станами явищ світу [21], тобто поміж формами існування матерії (простір-час, рух, взаємодія), в своїй основі спирається саме на єдність та взаємозв’язок зазначених форм існування матерії.

Наслідком такого внутрішнього зв'язку поміж геометричною та динамічною симетріями є існування узагальнених принципів симетрії, характерними ознаками яких є стабільність та точність. До таких принципів, в першу чергу, слід віднести принцип релятивістської симетрії (група Пуанкаре), в якій геометрична симетрія простору-часу (однорідність простору-часу та ізотропність простору) була пов’язана з динамічною симетрію (станом, рухом).

Узагальненістю та стабільністю відзначається і калібрувальна симетрія мікросвіту, пов’язана з законами збереження зарядів, тобто з інваріантністю внутрішніх квантових чисел.Зокрема, групу симетрій ізотопічного спіна I, яку ми віднесли до другого виду внутрішніх або динамічних симетрій (при розподілі симетрій на два види), можна виразити і в геометричний формі, адже саме взаємодії поміж квантовими мікрооб’єктами залишаються інваріантними стосовно будь-яких поворотів в ізотропічному просторі.

Однією з головних проблем фізики була і залишається проблема визначення глибокого внутрішнього взаємозв’язку поміж фізичними законами та їх симетрією. Без категорії симетрії неможливо дати повну характеристику категоріям закону, бо кожен закон містить в собі повну симетрію [21]. Слід пам’ятати, що при цьому симетрія визначає лише певну сторону фізичних законів.

Одним з можливих чинників порушення симетрії є процеси переходу структур одного типу до структур іншого типу в неорганічній природі, а також необоротні процеси самоорганізації в органічній природі, де завдяки додатному зворотному зв’язку, зміни в обраній системі накопичуються, підсилюються до такого рівня, що виникає нова структура (з іншим порядком та симетрією). Отже, процеси самоорганізації є необоротними і потребують іншої симетрії, яка не передбачає симетрію часу, характерну для оборотних процесів в замкнено-ізольованих системах класичної механіки. Більше того, наявність взаємозв’язку поміж фізичними законами можна охарактеризувати як їх симетрію „Симетрія законів – це суттєва сторона їх єдності, ...це наявність митті тотожності поміж зв’язками, що входять до їх змісту” [21].

У нерозривній єдності з симетрією знаходиться і така визначально-суттєва характеристика фізичних законів, як їх інваріантністьвідносно до певної сукупності змін, які притаманні відповідним природним явищам. Інваріантність фізичних параметрів (енергія, імпульс, момент імпульсу, заряд) або відповідних фізичних законів – це їх незмінність, незалежність від деяких фізичних умов. В математичному сенсі інваріантність означає незмінність певної величини відносно деяких перетворень. Інваріантність, як наслідок найбільш узагальнених симетрій, поряд з визначенням симетрії фізичних законів, виявляє і ступінь можливого узагальнення усіх законів, тобто межі їх застосування.

Саме інваріантність спричиняє існування таких узагальнених фундаментальних закономірностей природи як збереження енергії, імпульсу, заряду тощо. Слід пам’ятати, що інваріантність законів збереження, зумовлених певним типом симетрій, має місце і за умов можливих порушень цих симетрій.

Розглянемо більш детально взаємозв’язок принципів симетрії, інваріантності з законами збереження, як в класичній, так і в сучасній фізиці (фізиці останнього сторіччя).

У класичній фізиці ХVIIІ-ХІХ сторіч домінуючим був динамічний підхід відносно фізичних теорій, які розглядалися на підставі диференціальних рівнянь руху. При такому підході принципи інваріантності (принципи просторово-часової симетрії та закони збереження) відігравали другорядну роль відносно законів руху.

У сучасній фізиці вирішальне значення набув теоретико-інваріантний підхід, який зароджувався ще в ХVII сторіччі, (зокрема принцип Ферма в геометричній оптиці), але не набув достатнього розвитку і поступився динамічному підходу. Саме теоретико-інваріантна концепція є вирішальною для з’ясування структури сучасної фізичної теорії, яка ґрунтується натакихтрьох основах: 1) фундаментальній групі симетрій; 2) динамічному законі; 3) сукупності інваріантних параметрів фізичної теорії, які задовольняють відповідним законом збереження. При цьому явно виділяється домінуюча роль симетрії, яка, з одного боку, визначає форму динамічного закону, а з другого, „визначає кількість та тип незмінних величин” [58], тобто інваріантних параметрів.

Попередницею теоретико-інваріантного підходу в фізиці була подібна концепція в геометрії („Ерглангська програма”), згідно якій стало можливим упорядкування сукупності різних геометричних систем, визначення їх рівноправності. Вирішив цю задачу 23 річний Ф.Клейн шляхом розробки теорії інваріантів групи перетворень, внаслідок чого сукупність геометрій різного типу стала упорядкованою за ієрархічним принципом.

Передумовами застосування теоретико-інваріантної концепції в сучасній фізиці, як ефективного методологічного засобу (подібного до геометрії), були кардинальна зміна поглядів на роль принципів симетрії та усунення абсолютності часу t в різних системах відліку, тобто забезпечення своєрідної рівноправності всіх чотирьох поступово-часових параметрів (х, у, z, t) .

Саме спеціальна теорія відносності (СТВ), запропонована А.Ейнштейном в 1907-1908 рр., переконливо довела фундаментальну роль принципів інваріантності (принципу відносності та інваріантності швидкості світла). Подібна релятивістська симетрія передбачала ізотропність простору, поряд з існуючою однорідністю простору та часу. За такою симетрією чотиривимірного простору-часу закріпилася назва групи Пуанкаре, бо саме Пуанкаре, з’ясовуючи суть, універсальність релятивістської симетрії, приділив першочергову увагу ролі інваріантів перетворень Лоренца (зокрема просторово-часовому інтервалу) з одночасним визначенням групових властивостей цих перетворень (2.7-2.9).

Генрих Мінковський, шкільний вчитель А.Ейнштейна, запропонував геометричне трактування теорії свого учня на підставі відповідних діаграм. „Саме Мінковський був першим, хто явно та послідовно розповсюдив теоретико-інвариантне формулювання на СТВ, а згодом накреслив відповідну програму і для класичної механіки (1907-1908)”. Згодом Ф.Клейн довів замисел Мінковського до логічного завершення згідно розробленій ним ерглангській схемі в геометрії, що дало йому підстави для такого твердження: „Те, що сучасні фізики називають теорією відносності є теорією інваріантності чотиривимірного простору-часу х, у, z, t ” („світ” Мінковського) по відношенню до деякої певної групи перетворень, а саме „лоренцевої групи” [58].

З того часу, тобто вже майже сторіччя, теоретико-інваріантна концепція є визначальною при розробці нових теорій сучасної фізики у повній відповідності з вимогами релятивістської інваріантності, які діють на просторово-часовій різноманітності.

Будь-які варіанти теоретико-інваріантних концепцій спираються на три основні компоненти: фундаментальні групи симетрії, динамічні закони та сукупність інваріантних фізичних величин і передбачають залучення таких методологічних принципів, як принцип відповідності, простоти, доповнювальності. При цьому слід завжди враховувати емпіричний статут принципів симетрії, пам’ятаючи, що будь-які можливості теорії сучасної фізики (варіанти теоретико-інваріантного підходу) повинні надійно спиратися на експериментальні факти.

В зазначеному контексті надзвичайно важливу роль відіграють теореми Е.Нетер „...один з найважливіших засобів врахування емпіричного матеріалу при адекватному виборі симетрій і взагалі при побудові фізичних теорій, який встановлює взаємозв’язок фізичних симетрій з законами збереження [58]. Запропоновані Е.Нетер в 1918 р. дві теореми, завдяки їх математичній близькості, можуть бути розглянуті в теоретичній фізиці у вигляді узагальненої фундаментальної теореми, яка визначає взаємозв’язок поміж властивостями симетрії фізичної системи та законами збереження (інваріантності фізичних параметрів системи).

Теорема Нетер стверджує, що для певної фізичної системи рівняння руху (сукупність системи диференціальних рівнянь), можуть бути одержані на підставі варіаційного принципу механіки і при цьому кожному певному перетворенню(залежному від одного параметра системи), яке залишає інваріантним (незмінним) варіаційний функціонал, відповідає певний закон збереження.

Важливим є випадок, коли варіаційним функціоналом є дія S, яка являється однією з суттєвих характеристик руху механічної системи. В залежності від властивостей фізичної системи і від обраного способу опису руху цієї системи існують різні варіанти представлення дії S.

Зокрема дія згідно Гамільтону за проміжок часу 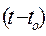визначається у вигляді 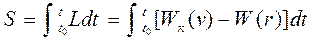, де 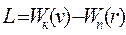– функція Лагранж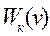а, та – кінетична та потенціальна енергія системи, відповідно. Саме в такому вигляді дія S входить в принцип найменшої дії в формі Гамільтона –Остроградського.

В принципі найменшої дії в формі Мопертюі-Лагранжа входить дія S по Лагранжу за проміжок часу 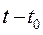, яка визначається в дещо іншому вигляді: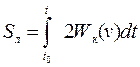

Принцип найменшої дії у будь-якій формі означає, що з сукупності можливих рухів, механічної системи поміж двома її положеннями в мить часу 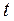та 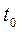реалізується лише той рух, для якого значення дії S являється найменшим ( ).

Досить нагадати траєкторію падіння тіл в полі земного тяжіння, ламану траєкторію променя світла в анізотропному середовищі. Отже, принцип найменшої дії в класичній фізиці є універсальним, всеохоплюючим для будь-яких змін, передбачаючи безперервну зміну класичної дії S до найменшої величини, охоплюючи і нульове значення.

В квантовому мікросвіті з його дискретною суттю, з існуючими закономірними перервностями роль універсального некласичного кванта найменшої дії з успіхом виконує стала Планка 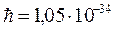Дж·с ≠ 0, яка є неодмінною ознакою будь-яких законів квантової механіки, в якій існують дві чітко визначені принципом неможливості обмеження, а саме швидкість розповсюдження будь-якого сигналу не може перевищувати 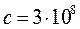м/с, а дія не може бути меншою, аніж квант найменшої дії 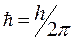. Саме зазначені неможливості є не лише основою для створення релятивістської 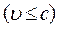та квантової механік, але й підгрунттям для розробки (згідно вимогам принципу відповідності) більш узагальненої квантової-релятивістської механіки.

На підставі методологічного принципу відповідності було доведено,що принцип Гамільтона є більш універсальним варіаційним принципом у порівнянні з принципом найменшої дії у механіці. Враховуючи той факт, що динамічні закони в сучасних фундаментальних фізичних теоріях теж мають варіаційну структуру, вони можуть бути сформульовані на підставі варіаційного принципу Гамільтона. З умови перетворення в нуль варіації дії 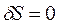знаходять рівняння руху фізичної системи. Таким чином, будь-який з диференційних законів збереження (інваріантності певної фізичної характеристики системи) відповідатиме кожному перетворенню при якому дія 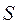не змінюється ( ).

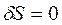У випадку просторово-часової (геометричної) симетрії до таких перетворень належать:

1) зсув у часі (однорідність часу), якому відповідає закон збереження енергії;

2) зсув у просторі (однорідність простору), з яким пов’язаний закон збереження імпульсу;

3) поворот у просторі (ізотропність простору), якому відповідає закон збереження моменту імпульсу.

В свою чергу інваріантність відносно перетворень Лоренца (2.7), на підставі теоремі Нетер, забезпечує узагальнений закон руху центра інерції (центра мас)системи, згідно якому швидкість цього центру .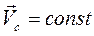

Надзвичайно важливим є той факт, що теорема Нетер може бути застосована не лише до просторово-часових (геометричних) симетрій, але й до симетрій іншого типу. Так, закон збереження електричного зарядуqпов’язаний з незалежністю динаміки заряджених об’єктів в електромагнітному полі відносно калібрувальних перетворень (одного з варіантів калібрувальної симетрії).

Теорема Нетер розкриває взаємозв’язок можливих форм прояву законів збереження з певними формами симетрії. „Так, відомі нам форми прояву закону збереження енергії, безумовно, пов’язані з однорідністю часу, але в цілому, цей закон може бути пов’язаний і з іншими, геометричними симетріями, поки що нам невідомими” [21].

Але найбільш суттєвим є висновок відносно того, що інваріантність загальних законів може бути пов’язана з симетріями різних груп перетворень. Закон збереження та перетворення енергії в своїх різних формах залишається інваріантним по відношенню до всіх груп перетворень і може бути пов’язаний з різними видами симетрії. „Симетрія однозначно інваріантність законів не визначає ” [21].

Таким чином, теорема Нетер забезпечила взаємозв’язок між трьома класами закономірностей, а саме: 1) симетрією; 2) динамічними законами у формі варіаційного принципу; 3) законами збереження, і тим самим дозволяє визначити цілісну структуру фізичних теорій (нетерову структуру). Подібна структура передбачає, що закони збереження є наслідком взаємозв’язку поміж першими двома компонентами теорії (симетрією та варіаційною формою динамічних законів). З’ясування зазначеного взаємозв’язку динамічного та кінематичного (просторово-часового) опису систем можливе на підставі методологічного принципу доповнювальності.

Надзвичайно важливим є те, що не лише фундаментальні теорії класичної фізики (нерелятивістської та релятивістської), але й теорії сучасної квантової фізики теж у більшості випадків задовольняють вимогам нетерової структури з тією лише відмінністю, що вона характеризується на квантово-механічній операторній мові [58].

Суттєве і те, що теорема Нетер відіграє важливу роль не лише при побудові структури фізичних теорій, але й для вирішення (хоча б часткового) основних методологічних проблем сучасної фізики. Прикладом цього є проблема збереження енергії –імпульсу в загальній теорії відносності (ЗТВ). Чітке визначення якої стало можливим лише на підставі теорем Нетер.

Важливим є внесок теорем Нетер і в проблематику фізики елементарних частинок, квантової теорії поля. При цьому використовується своєрідний аналог оберненої теореми Нетер, тобто на підставі емпірично виявлених законів збереження внутрішніх квантових чисел, або їх інваріантності (баріонний, та лептонний заряди, ізоспін, дивність, гіперзаряд, перність тощо) визначаються, конструюються відповідні цим законам збереження нові, невідомі типи симетрій. Саме такі симетрії виступають в якості необхідних умов, які обмежують ту чи іншу форму динамічного закону.

Отже проблема динамічного обґрунтування симетрії є однією з проблем фізики елементарних частинок. Більше того, і самі принципи симетрії, інваріантності потребують подальшого теоретичного обґрунтування.

Однак досягнутий нині рівень сучасної фізики переконливо свідчить, що саме принципи симетрії, інваріантності (в сукупності з принципами відповідності та доповнювальності) мають не лише евристичні та прогнозуючі функції, але є ефективними методологічними засобами побудови сучасних фізичних теорій, орієнтирами їх подальшого розвитку, одними з найбільш ефективних методів вирішення проблемних ситуацій в фізиці.

Запитання для самоперевірки

1. Яку функціональну роль відіграють апріорні, теоретичні та методологічні принципи науки?

2. В чому полягає комунікативна роль методологічних принципів, як засобів взаємозв’язку поміж філософськими та спеціальними науковими знаннями?

3. Які чинники визначають систематику та класифікацію методологічних принципів?

4. Які методологічні принципи є найбільш ефективними в філософсько-методологічній проблематиці сучасної науки?

5. Які методологічні принципи (з розглянутої сукупності) можуть розглядатися як універсальні метапринципи пізнання як неживої, так і живої природи?

6. Які методологічні принципи є принципами генезису та структурної побудови сучасних фундаментальних теорій?

Читайте також:

<== попередня сторінка	\|	наступна сторінка ==>
Принципи неможливості (заборони, вилучення)	\|	Тема 5. Онтологічна та гносеологічна проблематики постнекласичної науки

Не знайшли потрібну інформацію? Скористайтесь пошуком google:

Генерація сторінки за: 0.014 сек.