• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Плоский конденсатор

Рис 7.5

На довільній відстані x від стрижня напруженість електричного поля розраховується або за принципом суперпозиції (методом інтегрування), або за теоремою Гаусса. Скористаємось готовою формулою напруженості електричного поля (6.3.15) попередньої лекції

E = .

Підставимо це значення напруженості у формулу (7.3.2) та виконаємо інтегрування

dj = -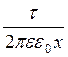dx, (7.3.6)

або

= - ,

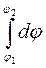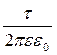
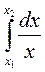звідки

j₁ - j₂ = 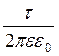ln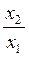. (7.3.7)

Аналогічно можуть бути виконані і будь-які інші розрахунки різниці потенціалів електричного поля статичних зарядів.

ЛЕКЦІЯ 8

ЕЛЕКТРИЧНЕ ПОЛЕ В ПРОВІДНИКУ. ЕЛЕКТРОЄМНІСТЬ

8.1. Провідник в електростатичному полі. Розподіл зарядів у провіднику.

8.2. Електроємність окремого провідника. Конденсатори. Електроємність конденсаторів різної форми.

8.3. Енергія взаємодії електричних зарядів. Енергія окремого провідника й конденсатора.

8.4. Енергія електростатичного поля. Густина енергії електростатичного поля.

8.1. Провідник в електростатичному полі. Розподіл зарядів у провіднику

У металевих провідниках завжди є вільні (не зв’язані з вузлами кристалічної гратки) електричні заряди. Переважно це валентні електрони, які слабо зв’язані з атомами в кристалічній структурі й за цієї причини стали колективізованими. Вільні електрони у провіднику перебувають у неперервному хаотичному русі, рівномірно заповнюючи весь об’єм провідника.

При внесенні такого провідника у зовнішнє електричне поле з сторони останнього на вільні електрони у провіднику, а також на вузли кристалічної гратки, які втративши частину валентних електронів і стали позитивними іонами, будуть діяти електричні сили. Під дією цих сил у провіднику відбувається перерозподіл електричних зарядів. Це призводить до виникнення власного електричного поля, направленого в протилеж-ному напрямку до зовнішнього електричного поля.

Перерозподіл зарядів у провіднику завершиться в той момент, коли внутрішнє поле повністю компенсує зовнішнє електричне поле. Будь-яка зміна величини зовнішнього електричного поля завжди закінчується адекватною зміною величини внутрішнього електричного поля. Так що результуюче поле у провіднику, згідно з принципом суперпозиції, буде дорівнювати нулю. (рис. 8.1).

На рис.8.1 у випадку а) тіло є нейтральним і не таким, у якому відсутні вільні електричні заряди. У випадку б) вільні електричні заряди провідника змістились і утворили власне електричне поле 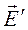, яке зрівноважило або знищило зовнішнє електричне поле 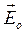. В цьому випадку поле у провіднику буде дорівнювати нулю, тобто

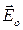+ = 0. (8.1.1)

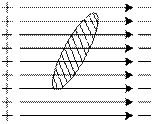
а) б)

Рис 8.1

Електричне поле 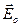провідником деформується. Силові лінії зовнішнього електричного поля входять у провідник перпендикулярно до його поверхні й виходять з провідника теж перпендикулярно до його поверхні.

Поверхня провідника є еквіпотенціальною, тобто поверхнею однакового потенціалу.

Якщо такому провіднику надати додатково електричні заряди величиною q, то і в цьому випадку всередині провідника електричне поле буде відсутнім. Це означає, що і ці електричні заряди електричним полем будуть перерозподілені по поверхні провідника. У провіднику, що перебуває у зовнішньому електричному полі, вільні електричні заряди перерозподіляються лише на його поверхні.

Цю властивість провідників використовують для електростатичного захисту чутливої електронної техніки. Корпуси різних електронних пристроїв виготовляють із провідників. Якщо такий корпус заземлити, то тим самим можна захистити електронні пристрої від будь-яких зовнішніх електричних і магнітних перешкод. Поверхня металевого корпусу стає еквіпотенціальною і добре виконує покладені на неї екрануючі властивості.

Важливо знати:

1. В стаціонарному стані направлений рух вільних зарядів у провіднику відсутній. Електричне поле у провіднику дорівнює нулю. Це означає, що хаотичний рух вільних електричних зарядів у провіднику ніколи не приводить до їх перерозподілу.

2. Якщо внести провідник у зовнішнє електричне поле, то власні вільні електричні заряди, а також додатково передані провіднику вільні електричні заряди за допомогою зовнішнього електричного поля будуть перерозподілятись по поверхні провідника до тих пір, доки своє внутрішнє електричне поле повністю не компенсує зовнішнє електричне поле. При цьому в першу чергу будуть перерозподілені додатково внесені електричні заряди.

3. Оскільки поверхня провідника є еквіпотенціальною, то елек-тричне поле 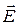, яке дорівнює , повинно бути перпендикулярним до поверхні в кожній точці провідника.

4. Поле 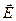на поверхні провідника не дорівнює нулю, однак це поле дорівнює нулю всередині провідника.

8.2. Електроємність окремого провідника. Конденсатори. Ємність конденсаторів різної форми

Надаючи провіднику різні електричні заряди можна виявити, що потенціал провідника при цьому змінюється пропорційно величині заряду, тобто

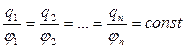. (8.2.1)

Цю сталу величину було названо електричною ємністю провідника. Таким чином, електрична ємність провідника дорівнює

С = , (8.2.2)

де q – заряд провідника, (додатково наданий провіднику); j - потенціал, під яким перебуває його поверхня.

Якщо провіднику був переданий заряд в 1Кл, а його потенціал при цьому змінився на 1В, то ємність такого провідника дорівнює 1Ф (Фарад).

Ємність у 1Ф досить велика. Практично використовують значно менші, кратні значення ємності:

1мкФ = 10^-6 Ф; 1пФ = 10^-12 Ф.

У випадку провідника сферичної форми електрична ємність буде дорівнювати:

С = ,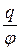

але ,

тому

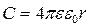. (8.2.3)

Ємність сферичного провідника визначається величиною його радіуса.

Для прикладу знайдемо радіус сферичного провідника, ємність якого буде дорівнювати 1Ф. З формули (8.2.3) маємо

.

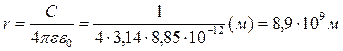Радіус такої кулі перевищує радіус Землі у 1400 разів.

Для практичних цілей ємність окремого провідника використовувати недоцільно через великі розміри. У цьому випадку використовують системи із двох окремих провідників, які називаються конденсаторами. Обидва провідники конденсатора заряджаються рівними за величиною і протилежними за знаком електричними зарядами.

Конденсатори бувають різні. Найбільш широко використовуються плоскі , циліндричні й сферичні конденсатори.

Для кожного типу конденсаторів справедливе співвідношення

, (8.2.4)

де 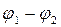- різниця потенціалів між двома окремими провідниками конденсатора; q – заряд кожного знаку на провідниках.

Знайдемо ємності окремих типів конденсаторів.

На рис.8.2 схематично зображений плоский конденсатор.

Рис.8.2

Плоский конденсатор складається із двох паралельних пластин площею S кожна, які розміщені на відстані d одна від одної. Заряди окремих пластин мають однакову поверхневу густину s, тобто

. (8.2.5)

Для знаходження різниці потенціалів у формулі (8.2.4) та визначення ємності плоского конденсатора скористаємось формулою (7.3.2) зв’язку напруженості електричного поля із потенціалом, тобто

Е = 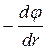. (8.2.6)

Напруженість електричного поля між двома пластинами плоского конденсатора перевищує напруженість електричного поля біля однієї площини у два рази (поля обох пластин збігаються за напрямком, а тому у відповідності з принципом суперпозиції накладаються). Тому у відповідності з формулою (6.3.3) маємо

, (8.2.7)

де - поверхнева густина зарядів.

Підставимо (8.2.7) у (8.2.6) і інтегруємо одержаний результат

,

,

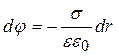. (8.2.8)

Підставимо (8.2.8) у (8.2.4), одержимо

.

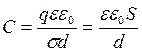Ємність плоского конденсатора буде дорівнювати

. (8.2.9)

З формули (8.2.9) видно, що величина ємності плоского конденсатора зростає при зростанні відносної діелектричної сталої e і площі пластини конденсатора S, а також при зменшенні відстані між пластинами конденсатора d. Електрична константа вакууму дорівнює e₀ = 8,85 ·10^-12 Ф/м.

Циліндричний конденсатор

Циліндричний конденсатор складається із двох циліндрів, розміщених один у одному, розділених шаром діелектричної речовини (рис.8.3).

Рис 8.3

Для знаходження ємності циліндричного конденсатора скористаємось формулами (8.2.4), (8.2.6) і (6.3.6). У цьому випадку внутрішню циліндричну частину можна вважати тонким, дуже довгим циліндром. Напруженість електричного поля біля такого циліндра на відстані r від осі у відповідності з формулою (6.3.6) буде дорівнювати (рис.8.4)

. (8.2.10)

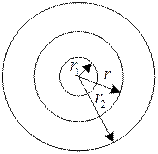
Рис.8.4

Підставимо вираз (8.3.10) у формулу (8.2.6), одержимо

.

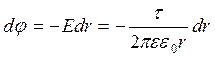Інтегруємо цей вираз в межах r від r₁ до r₂

,

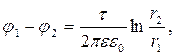(8.2.11)

де .

Вираз (8.2.11) підставимо у (8.2.4), одержимо ємність циліндрич-ного конденсатора

(8.2.12)

В цій формулі r₁, r₂ і h – параметри конденсатора у відповідності з рис.8.3 і 8.4. Діелектрична проникність e - залежить від властивостей діелектрика між циліндрами. Константа e₀ = 8,85 ·10^-12 Ф/м.

Читайте також:

1. Асинхронний генератор з конденсаторним збудженням.
2. Важливим параметром конденсаторів є пробивна напруга конденсатора. Чим вона більша, тим надійніший конденсатор, тим більша енергія може сконцентруватись на ньому.
3. Генератор папруги пилкоподібної форми без засобів стабілізації заряду конденсатора
4. Генератор папруги пилкоподібної форми зі стабілізацією струму заряду конденсатора
5. Енергія електричного поля конденсатора
6. Енергія зарядженого тіла і конденсатора. Енергія і густина енергії електричного поля
7. Енергія конденсатора
8. Енергія конденсатора
9. Ємність плоского конденсатора.
10. ІНТЕГРАТОРИ НА КОМУТАЦІЙНИХ КОНДЕНСАТОРАХ (КК).
11. Конденсатори
12. Конденсатори та їх сполучення.

Переглядів: 1755