• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция

Енергія зарядженого тіла і конденсатора. Енергія і густина енергії електричного поля

Розглянемо відокремлений провідник з електроємністю і електричним зарядом . Потенціал провідника рівний

. (3.116)

Перенесемо з нескінченності, де потенціал рівний нулю, елементарний заряд на поверхню провідника. При цьому електричним полем буде виконана робота

. (3.117)

Між однойменними електричними зарядами і діють сили відштовхування. Тому при наближенні елементарного заряду до заряду переміщення відбувається в напрямку протилежному до напрямку дії сили. Внаслідок цього електричне поле виконує від’ємну роботу.

Зміна потенціальної енергії рівна виконаній роботі з протилежним знаком, тобто

. (3.118)

Підставивши (3.116) в (3.118) і проінтегрувавши, дістанемо формулу енергії зарядженого провідника

, (3.119)

де А – постійна інтегрування. Будемо вважати, що енергія незарядженого провідника рівна нулю

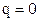; . (3.120)

Підставимо умови (3.120) у вираз (3.119) і визначимо постійну інтегрування А

. (3.121)

Підставимо (3.121) у формулу (3.119) і одержимо формулу потенціальної енергії зарядженого провідника

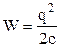. (3.122)

Використовуючи формулу (3.116) можна отримати інші формули для енергії зарядженого провідника:

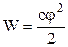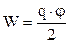; . (3.123)

Розглянемо конденсатор з електроємністю с, якому наданий електричний заряд q. Напруга між обкладками конденсатора рівна

. (3.124)

Перенесемо з однієї обкладки на іншу елементарний заряд dq. При цьому електричним полем буде виконана від’ємна робота, оскільки переміщення заряду dq здійснюється проти сили електричного поля

.

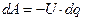Зміна потенціальної енергії конденсатора рівна виконаній роботі з протилежним знаком, тому вона рівна

. (3.125)

Підставимо (3.126) і використовуючи формулу (3.124) отримаємо формули енергії зарядженого конденсатора

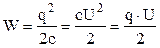. (3.127)

Знайдемо густину енергії зарядженого плоского конденсатора. Підставимо вираз для електроємності плоского конденсатора (3.103) у формулу (3.127)

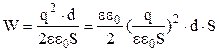. (3.128)

Введемо позначення

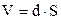, (3.129)

де v – об’єм простору між обкладками плоского конденсатора. Підставимо (3.129) і вираз (3.101) напруженості електричного поля всередині плоского конденсатора у формулу (3.128)

. (3.130)

Враховуючи зв’язок між напруженістю та індукцією електричного поля (3.7) формулу (3.130) можна представити також у вигляді

. (3.131)

Формули (3.130) і (3.131) виражають енергію зарядженого плоского конденсатора через такі характеристики електричного поля як напруженість та індукція, а також через об’єм простору в якому локалізоване електричне поле. Тому можна зробити висновок, що електричне поле володіє енергією.

Густиною енергії електричного поля називається фізична величина рівна енергії електричного поля в одиниці об’єму простору де міститься електричне поле

. (3.132)

Якщо електричне поле однорідне, то густину енергії електричного поля можна визначити за формулою

. (3.133)

Підставимо вирази (3.130) і (3.131) у формулу (3.133). отримаємо формули густини енергії електричного поля

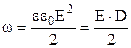. (3.134)

Із формули (3.132) визначимо диференціал енергії електричного поля

. (3.135)

Підставимо (3.134) в (3.135)

. (3.136)

Проінтегруємо вираз (3.136) по деякому об’єму

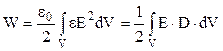. (3.137)

Ці формули дозволяють визначити енергію неоднорідного електричного поля.

Читайте також:

1. III. За виділенням або поглинанням енергії
2. IV. Критерій питомої потенціальної енергії деформації формозміни
3. Аналогія величин і рівнянь поступального і обертального руху. Кінетична енергія обертання тіла
4. Безпечні методи звільнення потерпілого від дії електричного струму.
5. В електронагрівачах використано одну з головних власти­востей електричного струму - здатність нагрівати провідники.
6. Важливим параметром конденсаторів є пробивна напруга конденсатора. Чим вона більша, тим надійніший конденсатор, тим більша енергія може сконцентруватись на ньому.
7. Види електричних травм та дії електричного струму на людину.
8. Визначення ймовірності перерви електропостачання і середньої кількості недоотриманої електроенергії.
9. ВИКОРИСТАННЯ СВІТЛОВОЇ ЕНЕРГІЇ ГАЛОБАКТЕРІЯМИ
10. Вимірювання електричного опору компенсаційним методом
11. Вимірювання електричного опору компенсаційним методом.
12. Вимірювання електричного опору методом амперметра-вольтметра

Переглядів: 3580