• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция

За теоремою Гаусса

. (6.3.14)

Прирівнюємо праві частини (6.3.13) і (6.3.14), одержимо

=.

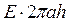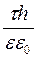Звідки

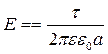, (6.3.15)

що збігається з формулою (6.3.6)

Висновок. Теорема Гаусса значно спрощує розрахунки, але має дуже вузькі рамки використання. Більш загальним, універсальним методом розрахунків напруженості електричного поля є метод суперпозиції, який у кінцевому випадку зводиться до інтегрування.

ЛЕКЦІЯ 7

ПОТЕНЦІАЛ ЕЛЕКТРОСТАТИЧНОГО ПОЛЯ

7.1. Циркуляція вектора напруженості .Теорема про циркуляцію вектора напруженості. Потенціальна енергія заряду.

7.2. Потенціал електростатичного поля. Різниця потенціалів. Принцип суперпозиції.

7.3. Зв’язок між потенціалом і напруженістю електростатич-ного поля . Приклади розрахунку полів.

7.1. Циркуляція вектора напруженості. Теорема про циркуляцію вектора напруженості. Потенціальна енергія заряду

Знайдемо роботу переміщення точкового заряду q_о в електричному полі точкового заряду q із точки 1 в точку 2 (рис 7.1)

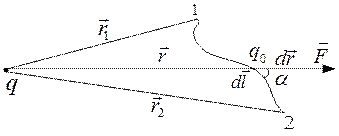
Рис 7.1

На елементарному переміщенні d силою 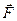виконується елементарна робота, яка дорівнює

dА = = F·dl·cosa = 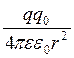dr, (7.1.1)

де dr=dl cos a - проекція переміщення d на напрям дії сили.

Інтегруємо вираз ( 7 .1 .1) в межах від r₁ до r₂ , одержимо

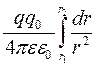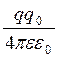
A_1,2 = = 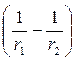. ( 7. 1. 2)

З формули ( 7 .1 .2) видно, що робота переміщення точкового заряду q_о із точки 1 в точку 2 поля статичного заряду q не залежить від форми шляху, а визначається лише положенням початкової й кінцевої точок.

Цей висновок є доказом того, що поле точкового заряду є потенціальним, а діючі в цьому полі сили є консервативними.

У випадку замкнутого контуру робота переміщення точкового заряду q_о в полі статичного заряду q буде дорівнювати нулю (рис 7.2).

Рис. 7.2

Елементарна робота сил поля на шляху d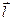дорівнює

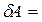qd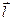= q_oEcosadl = q_oE_edl,

де E_e = Ecosa.

Робота перенесення точкового заряду q_o по замкнутому контуру в цьому випадку буде дорівнювати нулю

q_o= q_o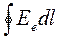=0. ( 7.1 .3)

Оскільки q_o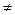0, то

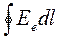= 0. ( 7. 1 .4)

Вираз (7. 1. 4) називають теоремою про циркуляцію вектора електростатичного поля вздовж будь-якого замкнутого контуру.

Силове поле, яке наділене такими властивостями, називають потенціальним полем.

Формула (7.1.4) має використання лише для статичних (нерухомих) зарядів.

В потенціальних полях робота консервативних сил виконується за рахунок зменшення потенціальної енергії.

Скориставшись формулою (7.1.2), виразимо роботу сил поля по переміщенню точкового заряду q_o з точки 1 в точку 2 поля заряду q, через потенціальні енергії заряду q_o, в цих точках ( рис 7 .1)

A_1,2 =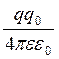= - = П₁ – П₂, (7.1.5)

де П₁ = - потенціальна енергія заряду q₀ в точці 1 поля точкового заряду q;

П₂ = - потенціальна енергія заряду q_o в точці 2 поля точкового заряду .

Або виразимо цю роботу через зменшення потенціальної енергії, при перенесенні заряду q₀ з точки 1 в точку 2, тобто

А_1,2 = - ( П₂ – П₁ ) . ( 7. 1. 6)

Якщо поле створюється системою точкових зарядів, то потенціальна енергія заряду q_o, в полі системи точкових зарядів q,_i матиме вигляд

П = q_o. (7.1 .7)

Важливо знати,що для однойменних зарядів потенціальна енергія їх взаємодії завжди додатна, а потенціальна енергія взаємодії різнойменних зарядів завжди від’ємна.

7.2. Потенціал електростатичного поля. Різниця потенціалів. Принцип суперпозиції

В лекціях з розділу “Механіка“ потенціальна енергія матеріальної точки або тіла визначалась через роботу переміщення тіла з будь-якої точки поля в деяке фіксоване положення, вибране за нульове положення, тобто

= П . ( 7.2.1)

Для електричних зарядів сила = q_o, тому

q_o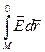= П . ( 7.2.2.)

З рівності (7.2.2) можна зробити висновок, що відношення = const, тобто який би заряд q_i не розміщувати в поле іншого заряду, відношення потенціальної енергії заряду q_i до величини цього заряду для даної точки поля буде величиною сталою. Цю величину називають потенціалом і позначають буквою j , тобто

j = . (7. 2. 3)

Потенціал j в будь-якій точці електростатичного поля є скалярною величиною, яка визначається потенціальною енергією позитивного пробного заряду, поміщеного в цю точку.

З урахуванням формули (7 .1. 5) потенціал поля точкового заряду q буде дорівнювати

j = 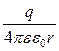. ( 7. 2. 4 )

При переміщенні одиничного позитивного заряду з точки 1 поля в точку 2 виконану роботу можна виразити спочатку через різницю потенціальних енергій, а потім і через різницю потенціалів поля в цих точках, тобто

A_1,2 = П₁ – П₂ = q_o (j₁ - j₂) =q_o Dj. ( 7. 2. 5 )

Різниця потенціалів в двох точках поля j₁ - j₂ визначається роботою сил поля по переміщенню точкового позитивного заряду із точки 1 в точку 2, тобто

j₁ - j₂ = . ( 7. 2. 6 )

Якщо вибрати точку 2 за межами поля, скажемо на безмежності, то й потенціал поля там буде дорівнювати нулю. Тому потенціал поля точкового заряду з цих міркувань можна виразити ще й так:

j = , ( 7. 2. 7 )

де A_1,¥ - робота переміщення заряду q_o з даної точки 1 в безмежність; q_o - точковий позитивний заряд.

Потенціал точкового заряду, так само як і різниця потенціалів, вимірюється в Дж/Кл або вольтах ( В ).

Для системи точкових зарядів потенціал поля в довільний точці поля цих зарядів визначається за допомогою принципу суперпозиції полів, тобто

j = , ( 7. 2. 8)

де j_I – потенціал і -го заряду в цій точці поля.

Потенціал поля системи електричних зарядів дорівнює алгебраїчній сумі потенціалів полів всіх цих зарядів. У випадку просторового розміщення системи електричних зарядів, потенціал поля цих зарядів знаходиться шляхом інтегрування.

Розглянемо приклад розрахунку потенціалу просторово розміщених електричних зарядів. Для цього знайдемо потенціал поля рівномірно зарядженого стрижня довжиною l з лінійною густиною зарядів t, в точці А, яка перебуває на продовженні осі стрижня на відстані а від його кінця (рис. 7.3).

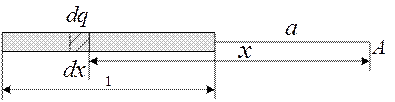
Рис 7.3

На стрижні виділимо безмежно малу ділянку, довжиною dx із зарядом dq, для якої потенціал в точці А можна записати, як для точкового заряду, а саме

dj = . (7.2.9)

Величина точкового заряду dq дорівнює tdx, тому

dj = . (7.2.10)

Проінтегруємо цей вираз в межах зміни x від а до a+l, тобто

j = 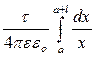= ln .

Аналогічно можна виконувати розрахунки потенціалу просторово розміщених електричних зарядів та в інших випадках

7.3. Зв’язок між потенціалом і напруженістю електростатич-ного поля. Приклади розрахунку полів

Як уже показано вище, робота переміщення одиничного позитивного заряду q_o в полі заряду q, виконується за рахунок зменшення потенціальної енергії, тобто

А_1,2 = П₁ – П₂ = -(П₂ – П₁) = -q(j₂ - j₁).

Запишемо цю роботу для безмежно малого переміщення, на якому електричний потенціал змінюється на безмежно малу величину

dА = -q_odj,

і

dА = q_o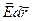. (7.3.1)

Прирівняємо праві сторони рівностей (7.3.1), одержимо зв’язок між потенціалом і напруженістю електростатичного поля:

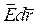= -dj,

звідки

E = -. (7.3.2)

Сам потенціал dj є величиною скалярною, а градієнт зміни потенціалу в певному напрямі є величиною векторною.

В більш загальному випадку просторового переміщення точкового заряду формула (7.3.2) набуває вигляду

= -j = -j,

де - вектор, який має назву оператора Гамільтона або його ще називають “набла”.

Оператор є вектором, який також можна записати так

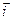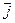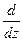
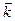= + + , (7.3.3)

де 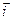,,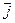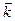- одиничні вектори в напрямку осей x,y,z декартової системи координат.

Знайдемо різницю потенціалів j₂ - j₁, в двох точках поля біля безмежної поверхні з поверхневою густиною зарядів s у відповідності з рисунком (рис.7.4)

Рис 7.4

Скористаємося формулою (7.3.2) зв’язку напруженості електрич-ного поля з потенціалом, одержимо

dj = -Edr. (7.3.4)

Напруженість поля E біля безмежної поверхні розрахована в шостій лекції (6.3.3), тому скористаємось готовим результатом, який дорівнює

E = .

Тоді

dj = -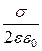dr.

Інтегруємо цей вираз в межах зміни координати від x₁ до x₂ і зміни потенціалу від φ₁ до φ₂, одержимо

= -,

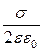
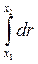звідки

j₂ - j₁ = -(x₂ – x₁),

або

j₁ - j₂ = (x₂ – x₁). (7.3.5)

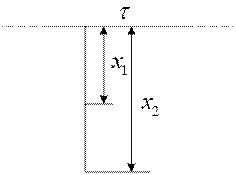
2. Потенціали поля в двох точках біля довгого, рівномірно зарядженого стрижня з лінійною густиною зарядів t у відповідності з рисунком (рис. 7.5)

Читайте також:

1. Використання карти великого масштабу проекції Гаусса-Крюгера
2. ЗАСТОСУВАННЯ ТЕОРЕМИ ОСТРОГРАДСЬКОГО - ГАУССА
3. Метод Гаусса знаходження оберненої матриці.
4. Метод Гаусса-Зейделя
5. Напряженность поля. Теорема Гаусса
6. ТЕОРЕМА ОСТРОГРАДСЬКОГО - ГАУССА

Переглядів: 966