• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция

З рисунка видно, що

Рис. 6.7

З рисунка видно, що x² = z² + r², а dq = rda drs, й dE_z = dEcosj.

З урахуванням цих позначень одержуємо:

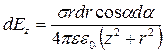. (6.3.2)

Але оскільки соsj = 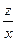, тому

.

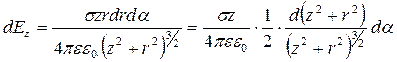Інтегруємо цей вираз у межах: для r від 0 до 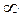; для a від 0 до 2p, одержимо:

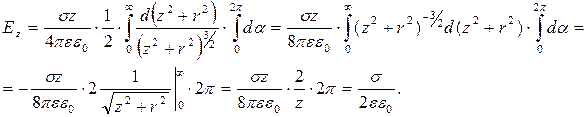
З розрахунків видно, що напруженість електричного поля біля безмежної, рівномірно зарядженої площини з поверхневою густиною зарядів s, визначається досить простою формулою і не залежить від відстані до самої площини

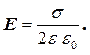(6.3.3)

Приклад 2. Визначити напруженість електричного поля на відстані а від тонкої, досить довгої, рівномірно зарядженої, із лінійною густиною зарядів t нитки або циліндра (рис 6.8).

Рис. 6.8

Скористаємось формулою (6.2.6)

dE = .

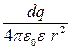З рисунка видно, що: dq = tdl і dS = rda, а також dS = dl·cosa.

З урахуванням цих залежностей одержуємо величину точкового заряду:

dq = 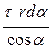. (6.3.4)

Тоді напруженість електричного поля у напрямі осі у E_y – буде дорівнювати

dE_y = dEcosa = = .

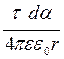Величину радіуса-вектора r виразимо через відстань а і кут a:

r = .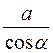

З урахуванням останнього одержимо:

dE_y = . (6.3.5)

Інтегруємо останній вираз у межах зміни a від 0 до , помноживши весь вираз на 2 (враховується друга, симетрична частина нитки).

.

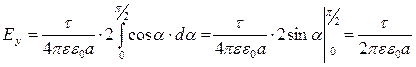Таким чином одержано досить просту залежність напруженості електричного поля біля довгої, рівномірно зарядженої нитки або циліндра:

Е = 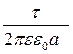. (6.3.6)

Паралельна складова напруженості Е_x, завдяки симетричності нитки, буде дорівнювати нулю.

Знайдемо потік вектора 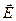напруженості електричного поля крізь замкнену поверхню ( рис. 6.9)

Рис. 6.9

, (6.3.7)

де 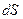- величина площі заштрихованої поверхні, 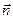- нормаль до поверхні (одиничний вектор).

де 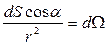- тілесний кут.

Площа поверхні кулі (тут 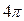є тілесним кутом).

Таким чином одержуємо:

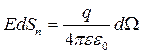. (6.3.8)

Інтегруємо цей вираз у межах замкнутої поверхні і повного тілесного кута для цієї поверхні, тобто

.

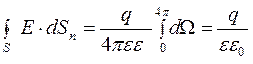Одержаний вираз носить назву теореми Гаусса

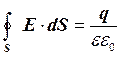. (6.3.9)

Якщо замкнута поверхня охоплює систему зарядів, теорема Гаусса набуде вигляду

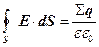. (6.3.10)

Потік вектора напруженості електричного поля крізь довільну замкнуту поверхню дорівнює алгебраїчній сумі всіх зарядів у середині цієї поверхні, поділених на ee₀.

Покажемо на прикладах, як використовується теорема Гаусса у найпростіших випадках.

Приклад 1. Електричне поле біля безмежної, рівномірно зарядженої, із поверхневою густиною зарядів σ, площини ( рис. 6.10).

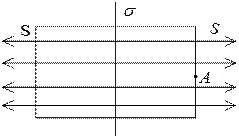
Рис. 6.10

На рисунку заряджена площина спроектована перпендикулярно до площини листка. Замкнена поверхня є циліндром із площею торців S. Потік вектора напруженості в даному випадку слід розрахувати лише крізь торці. Лінії напруженості електричного поля паралельні до бокової поверхні, а тому потоку не створюють, тобто

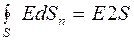. (6.3.11)

За теоремою Гаусса

. (6.3.12)

Прирівнявши праві сторони (6.3.11) і (6.3.12) одержимо:

.

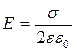Цей висновок збігається з формулою (6.3.3).

Приклад 2. Електричне поле на відстані a від довгої, рівномірно зарядженої з лінійною густиною зарядів τ, нитки (рис. 6.11).

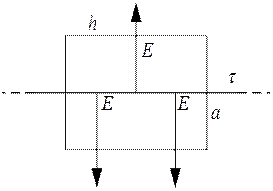
Рис. 6.11

На рисунку замкнуту поверхню вибрано у вигляді циліндра радіусом а і довжиною h. Потік силових ліній слід розглядати лише крізь бокову поверхню, так як торці перпендикулярні до нитки й паралельні до напрямку силових ліній електричного поля. (Потік крізь торці в цьому випадку дорівнює нулю).

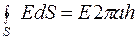. (6.3.13)

Читайте також:

1. Видно, що ,( тобто площина паралельна до осі Ox.
2. Виконання усних вправ за готовими рисунками
3. Примітка:Панель інструментів Малювання здебільшого розташована внизу екрана. Якщо цієї панелі не видно, в меню Вигляд виберіть команду Панелі інструмен­тів Малювання

Переглядів: 919