
РЕЗОЛЮЦІЯ: Громадського обговорення навчальної програми статевого виховання
ЧОМУ ФОНД ОЛЕНИ ПІНЧУК І МОЗ УКРАЇНИ ПРОПАГУЮТЬ "СЕКСУАЛЬНІ УРОКИ"
ЕКЗИСТЕНЦІЙНО-ПСИХОЛОГІЧНІ ОСНОВИ ПОРУШЕННЯ СТАТЕВОЇ ІДЕНТИЧНОСТІ ПІДЛІТКІВ
Батьківський, громадянський рух в Україні закликає МОН зупинити тотальну сексуалізацію дітей і підлітків
Відкрите звернення Міністру освіти й науки України - Гриневич Лілії Михайлівні
Представництво українського жіноцтва в ООН: низький рівень культури спілкування в соціальних мережах
Гендерна антидискримінаційна експертиза може зробити нас моральними рабами
ЛІВИЙ МАРКСИЗМ У НОВИХ ПІДРУЧНИКАХ ДЛЯ ШКОЛЯРІВ
ВІДКРИТА ЗАЯВА на підтримку позиції Ганни Турчинової та права кожної людини на свободу думки, світогляду та вираження поглядів
- Гідрологія і Гідрометрія
- Господарське право
- Економіка будівництва
- Економіка природокористування
- Економічна теорія
- Земельне право
- Історія України
- Кримінально виконавче право
- Медична радіологія
- Методи аналізу
- Міжнародне приватне право
- Міжнародний маркетинг
- Основи екології
- Предмет Політологія
- Соціальне страхування
- Технічні засоби організації дорожнього руху
- Товарознавство продовольчих товарів
Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция
Ємність плоского конденсатора.
7.
5.
4.
Елементарна робота dA, яка виконується силою 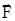 =q0
=q0 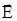 при переміщенні заряду q0 на відрізок d
при переміщенні заряду q0 на відрізок d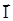
|
dA=(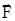 d d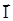 )=(q0 )=(q0 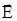 d d ) =q0Edl ×cos a = q0 E dr
Робота, яку виконує електричне поле при переміщенні заряду q0 з точки 1 (r1) у точку 2 (r2) ) =q0Edl ×cos a = q0 E dr
Робота, яку виконує електричне поле при переміщенні заряду q0 з точки 1 (r1) у точку 2 (r2)
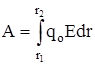 або або
|
A=( q0q /4p e0 e)(1/r1- 1/r2) ( 11 )
З (11) видно, що робота не залежить від форми шляху, а залежить тільки від початкового та кінцевого положеня точок. Висновок: сили електростатичного поля консервативні, а саме поле потенціальне.
dA = q0 ( 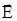 d
d );
);
 (
( 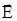 , d
, d ) - циркуляція вектора
) - циркуляція вектора 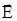 по замкненому контуру L.
по замкненому контуру L.
A = q0  (
( 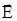 ,d
,d );
);
Із формули (11) видно, що робота електричного поля по замкненому контуру ( r1= r2 ) дорівнює нулю. Таким чином, із визначення циркуляції виходить, що вона дорівнює нулю.
Якщо циркуляція вектора будь-якого силового поля дорівнює 0, то як наслідок силові лінії такого поля не замкнені.
Із розділу механіки відомо, що робота консервативних сил виконується за рахунок змін потенціальної енергії;
A = - DWn = - ( Wn(2) - Wn(1)) = Wn(1) - Wn(2) (12)
Wn – потенціальна енергія заряду.
Wn(2) – потенціальна енергія заряду в точці 2.
Wn(1) – потенціальна енергія заряду в точці 1.
Із рівняння (12) і (11)
Wn = qq0 /(4p e0 e r) + c ;
c = 0 ( r ®  )
)
Wn = qq0 /(4p e0 e r) ; (13)
Потенціалом j даної точки поля називається відношення потенціальної енергії Wn заряду q0 у даній точці до величини цього заряду.
j = Wn / q0 ; (14)
Із (14) видно, що потенціал — це енергетична характеристика даної точки поля. Знайдемо зв’язок між 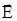 та j. Для цього перемістимо заряд q0 між двома близькими точками простору.
та j. Для цього перемістимо заряд q0 між двома близькими точками простору.
dA = q0 E dl ; dA = - d Wn;
dA = - q0 dj; q0Edl = - q0 dj;
El = - (dj /dl); 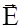 = - (dj /dl)
= - (dj /dl)  ; (15)
; (15)
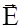 = - (dj /dl)
= - (dj /dl)  ;
;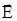 = -
= -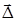 j = - grad j;
j = - grad j;
Напруженість поля в даній точці дорівнює градієнтові потенціалу, взятому з протилежним знаком.
Будь-яка точка електричного поля характеризується як векторною, так і скалярною величинами (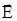 та j), між якими існує певний зв’язок.
та j), між якими існує певний зв’язок.
6. Якщо помістити провідник у зовнішнє електричне поле, то вільні заряди (наприклад- d електрони у металі) перерозподіляться такими чином, що напруженість електричного поля у середині провідника буде дорівнювати нулю.
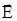 рез = 0 ; Е = - (dj /dl);
рез = 0 ; Е = - (dj /dl);
Е = 0 ; (dj /dl) = 0 ; j = const ,
як у середині провідника, так і на його поверхні, тобто весь об’єм провідника, можна вважати еквіпотенціальним,а напруженість електричного поля біля поверхні завжди буде спрямована по нормалі до поверхні у даній точці.
Якщо надати провіднику додатковий електричний заряд, то нескомпенсовані заряди розмістяться тільки на поверхні провідника.
Ця властивість застосовується для електростатичного екранування від зовнішніх електричних полів.
Можна показати, що напруженість електростатичного поля поблизу поверхні провідника прямо пропорційна поверхневій густині заряду s:
s = q / S; Еn = s / e0 e ; (16)
Як показує досвід, при нанесенні на відокремлений провідник заряду для однакових провідників зі зростанням величини заряду q буде зростати і потенціал цього провідника j. Тому для відокремленого провідника:
j = ( 1/С ) q ; (17)
де С – ємність відокремленого провідника
С = q / j; (18)
[ C ] = Кл / В = Ф.
Ємність залежить від геометричної будови провідника (його форми та лінійних розмірів) ті діелектричної проникності середовища, в якому він знаходиться.
Для сфери: С = 4p e0 e R , де R – радіус сфери.
Конденсатор– це система, що являє собою два провідники, які розділені шаром діелектрика.
С = e0 e S / d ; (19)
e0 – електрична стала;
e – діелектрична проникність;
S – площина однієї з пластин плоского конденсатора;
d – відстань між пластинами;
Паралельне з”єднання конденсаторів:





 Срез = С1 + С2 ;
Срез = С1 + С2 ;
Читайте також:
- Важливим параметром конденсаторів є пробивна напруга конденсатора. Чим вона більша, тим надійніший конденсатор, тим більша енергія може сконцентруватись на ньому.
- Втискування плоского циліндричного індентора
- Енергія зарядженого тіла і конденсатора. Енергія і густина енергії електричного поля
- Ємність кабеля
- Ємність у ланцюзі синусоїдального струму
- Застереження про взаємність у міжнародному приватному праві.
- Капілярна вологоємність та методи її визначення
- Киснева ємність крові. Газообмін між кров’ю та тканинами.
- Конденсатори. Електроємність конденсатора. З’єднання конденсаторів
- Можна легко створити електростатичне поле між двома металевими обкладинками конденсатора.
- Неважко визначити показник політропи та теплоємність т.-д. с. для різних т.-д. процесів.
| <== попередня сторінка | | | наступна сторінка ==> |
| Механізм взаємодії | | | Енергія конденсатора |
|
Не знайшли потрібну інформацію? Скористайтесь пошуком google: |
© studopedia.com.ua При використанні або копіюванні матеріалів пряме посилання на сайт обов'язкове. |
