• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Умовна ентропія

Повідомлення а і b, є статистично залежними, якщо існує ймовірність появи повідомлення b за умови, що вже з’явилось повідомлення а або навпаки. Мірою порушення статистичної незалежності між повідомленнями а і b є умовна ймовірність появи повідомлення а за умови, що вже з'явилося повідомлення b: p(a/b),або умовна ймовірність появи повідомлення b, коли вже з'явилося повідомлення а: р(b/а),причому взагалі p(a/b) ≠ р(b/а).

Теорія математичної статистики визначає умовну ймовірність через безумовні ймовірності p(а), р(b) тасумісну безумовну ймовірність p(ab) за законом множення ймовірностей:

р (ab) = p (a) p (b/a) = p (b) p (a/b). (7)

Звідси випливає, що

р (b/а) = р (ab) / р (а); р (a/b) = р (ab) / p (b). (8)

Умовною називають ентропію джерела повідомлень, яке містить статистично залежні повідомлення.

Розрізняють два різновиди умовної ентропії: часткову та загальну.

Для алфавітів (джерел) повідомлень

A = {a₁, a₂, ..., a_i, ...,a_k} та B= {b₁, b₂, ..., b_j, ..., b_l}

часткова умовна ентропія:

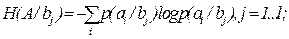(9)

(10)

де а_і — конкретне повідомлення, відносно якого визначається часткова умовна ентропія Н(B/a_i) алфавіту В за умови вибору попереднього повідомлення a_i, b_j — конкретне повідомлення, відносно якого обчислюється часткова умовна ентропія Н(A/b_j) алфавіту А за умови вибору попереднього повідомлення b_j, і — номер повідомлення з алфавіту A; j — номер повідомлення з алфавіту В; р(a/b), р(b/а) — умовні ймовірності.

Алфавіти А та В можуть бути однакового (k = l) і різного (k ≠ l) обсягів.

При умові співпадання алфавітів А та В (А = В), часткову ентропію використовують для аналізу взаємозв’язку повідомлень одного і того ж джерела. Такі послідовності зумовлених повідомлень називають ланцюгами Маркова.

Статистична залежність джерела В від джерела А описується матрицею прямих переходів повідомлень a_і(і = 1 ... k) джерела А в повідомлення b_j (j = 1 ... k) джерела В:

Матриця відбиває вплив завад у каналі між джерелом А та спостерігачем В. Якщо завади непомітні або зовсім відсутні, то маємо однозначну відповідність а_i → b_i з умовної ймовірності p(b_i/a_i) = 1 для i = 1 ... k. Решта ймовірностей p(b_j/a_i) = 0 для всіх j ≠ і.

Кожний рядок матриці є спотвореним розподілом імовірностей Р_В появи повідомлення b_j В. Джерело В має розподіл безумовних імовірностей Р_В. Врахування статистичного впливу повідомлення а_i А спотворює цей розподіл (або уточнює його) і дає новий розподіл імовірностей Р (В/а_і) для і-горядка матриці. Саме тому виконується закон нормування

, і = 1…k. (11)

Читайте також:

1. А — позитивна умовна реакція натискання на клавішу, В — бурхлива емоційно-рухова реакція за відсутності харчового підкріплення сигналу.
2. Абсолютна ентропія
3. Джерело дискретних повідомлень і його ентропія
4. Ентропія
5. Ентропія д. в. в. X
6. Ентропія дискретної величини
7. Ентропія є мірою розсіяної (знеціненої) енергії, ентропія системи – це міра невпорядкованості її стану.
8. Ентропія і імовірність
9. Ентропія, енергія Гіббса та напрямленість процесів
10. Кількість інформації по Шенону. Ентропія, як міра невизначеності інформації, та її властивості
11. Самодовільних процесів. Ентропія
12. У випадку відкритих систем ентропія може змінюватися як завгодно.

Переглядів: 2673