• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Предикати

Вживані в математиці вислови|висловлювання| звичайно є описом властивостей яких-небудь математичних об'єктів або описів відносин, що існують|наявний| між цими об'єктами. Для аналізу закономірностей, властивих таким висловам|висловлюванням|, засобів|коштів| алгебри висловів|висловлювань| вже недостатньо. Тому вводиться|запроваджується| поняття предиката.

Індівідна (або наочна|предметна|) змінна є знаком, який позначає|значити| довільний індивід з|із| деякої непорожньої підмножини безлічі всіх індивідів; ця підмножина називається областю зміни даної змінної.

Хай|нехай| 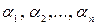– індивіди з|із| наочної|предметної| області I. Розглянемо|розгледимо| який-небудь вислів|висловлювання| про цих індивідів і позначимо його через P(). Якщо n = 1, то P() виражає|виказує,висловлює| властивість індивіда . Якщо n ³2, то даний вислів|висловлювання| описує деяке відношення|ставлення| між індивідами 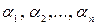(порядок|лад| проходження|дотримання| індивідів має значення|).

Візьмемо наочні|предметні| змінні (з|із| областями зміни відповідно; тут – підмножина множини|безлічі| I 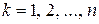). Вираз|вираження| P() – і є предикат. Тут P може позначати|значити| конкретний предикат (тобто константу) або змінну-предикат, тобто предикат в його основному сенсі|змісті,рації|. Предикат, залежний в точності від n різних наочних|предметних| змінних, називається n-місцевим. Вислів|висловлювання| можна розглядати|розглядувати| як нуль-місцевий| предикат, тобто як предикат, не залежний від наочних|предметних| змінних.

Приклад|зразок| 2.3. «x є парне число» – одномісний предикат; « x є дільник y» – двомісний (бінарний) предикат.

Хай|нехай| P() – предикат, а – індивідуальна константа 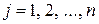; тоді вираз|вираження| P(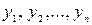) – називається елементарною формулою.

Приклад|зразок| 2.4. Розглянемо|розгледимо| бінарні індивідуальні предикати: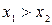, і 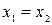. Символи „>”, „ê”і „=” означають, як завжди, «більше», «є дільник», «рівно». Вирази >3,75 і є|з'являються,являються| елементарними формулами.

З|із| елементарними формулами можна оперувати так само, як і з пропозиціональними|із|| змінними: до ним застосовні всі операції алгебри висловів|висловлювань|. За допомогою логічних зв'язок|в'язок| з|із| елементарних формул будуються нові, предикативні формули. Самі елементарні формули теж|також| вважаються|лічаться| предикативними.

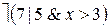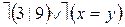Приклад|зразок| 2.5.і – предикативні формули. Їх можна «прочитати» таким чином: першу – «невірно, що 7 – дільник 5 і x більше 3», другу – «3 не ділить 9 або x не рівно».

Використання тільки|лише| елементарних формул і операцій алгебри висловів|висловлювань| не дає можливість|спроможність| подолати|здолати| труднощі, що виникають, наприклад, при спробі сформувати на формальній логіко-математичній мові|язиці| наступну|слідуючу| теорему: «рівняння x+3=8 має цілочисельне рішення|розв'язання,вирішення,розв'язування|». У зв'язку з цим в розгляд вводяться|запроваджуються| квантори. Використовують два квантори: спільності (позначення:; читається: «для всіх...») і існування (позначення: 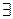; читається: «існує...»).

Таким чином, предикативні формули будуються з|із| елементарних формул за допомогою логічних зв'язок|в'язок| і кванторів загальності і існування. Застосування|вживання| кванторів для побудови|шикування| формул здійснюється по наступній|такій| схемі. Хай|нехай| Н – предикативна формула і x – наочна|предметна| змінна, яка може і не входить у формулу Н. 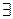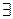Тоді вирази|вираження| (xH) і (xH) вважаються|лічаться| предикативними формулами (в цьому випадку говорять, що Н є область дії відповідного квантора x або x).

Приписування спереду до предикативної формули якого-небудь квантора називається операцією навішування квантора (або скріплення|зв'язування| квантором). Конкретне входження змінної x у формулу Н називається зв'язаним, якщо воно або безпосередньо слідує|прямує| за яким-небудь|будь-яким| квантором, або міститься|утримується| у області дії деякого квантора x або 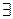x. Якщо входження змінної у формулу не є|з'являється,являється| зв'язаним, то воно називається вільним. Змінна, що входить у формулу Н, називається зв'язаною (вільною), якщо в Н є|наявний| зв'язане (вільне) входження цієї змінної. Таким чином, змінна може бути одночасно і вільної і зв'язаної (у даній формулі).

Приклад|зразок| 2.6. Хай|нехай| Z – безліч цілих чисел. У предикативній формулі 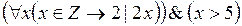змінна x є|з'являється,являється| і зв'язаною (три її входження в перший член кон'юнкції – зв'язані), і вільною (входження x у формулу x > 5 – вільне). Областю дії квантора x є|з'являється,являється| формула

У формулі , що є дійсним висловом|висловлюванням|, всі три входження змінної x – зв'язані.

Читайте також:

1. МОДУЛЬ 2: «Висловлення. Предикати. Теореми.».
2. МОДУЛЬ 2: «Висловлення. Предикати. Теореми.».
3. Предикати

Переглядів: 808