• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция

Перешкодостійке кодування

Хай|нехай| є|наявний| канал зв'язку C, що містить|утримує| джерело перешкод:

,

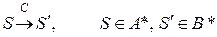де S – безліч переданих, а 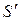– відповідна безліч прийнятих по каналу повідомлень|сполучень|. Кодування F, що володіє такою властивістю, що

,

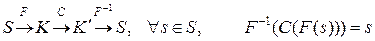називається перешкодостійким.

Якщо A=B={0,1}, то помилки в каналі можуть бути наступних|слідуючих| типів:

· 0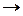1, 1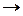0 – помилка типу заміщення розряду;

· 0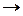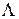, 1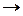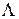– помилка типу випадання розряду;

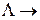· 1, 0 – помилка типу вставки розряду.

Хай|нехай| 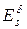– безліч слів, які можуть бути одержані|отримані| із|із| слова s в результаті|унаслідок,внаслідок| всіх можливих комбінацій допустимих в каналі помилок 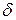, тобто|цебто| 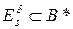. Якщо 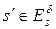, то та конкретна послідовність помилок, яка дозволяє одержати|отримати| із|із| слова s слово 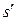, позначається|значиться| 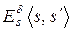. Якщо тип можливих помилок в каналі мається на увазі, то індекс 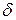не указується|вказується|.

Теорема 7.3. Щоб існувало перешкодостійке кодування з|із| виправленням всіх помилок, необхідне і досить|достатньо|, щоб 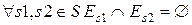, тобто|цебто| необхідне і досить|достатньо|, щоб існувало розбиття множини|безлічі| B* на множини 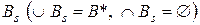|безліч|, таке що .

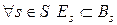Доказ. Якщо кодування перешкодостійке, то очевидно, що 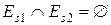. Назад: по розбиттю 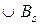будується функція .

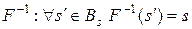Розглянемо|розгледимо| множину|безліч| 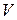зі|із| всіх 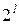двійкових послідовностей (векторів), що мають вигляд|вид|

.

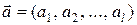Введемо|запровадимо| в множині|безлічі| 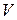операцію складання +, визначивши для послідовностей 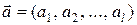і 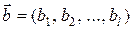їх суму за допомогою співвідношення: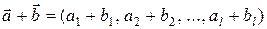, де 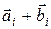– це сума по модулю два.

Відстань Хеммінга 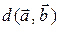між кодовими словами визначається як число позицій 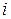таких, що 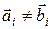. При побудові|шикуванні| вектора 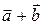пари однакових двійкових символів 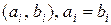даватимуть 0, а пари різних двійкових символів даватимуть 1.

Приклад|зразок| 7.4.(0, 1, 0, 1)+(1, 1, 1, 0)=(1, 0, 1, 1).

Тому відстань Хеммінга 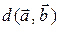можна визначити як число компонент вектора, які рівні 1.

Введена|запроваджена| таким чином відстань Хеммінга задовольняє наступним|слідуючим| умовам:

·

· ;

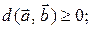
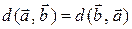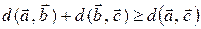· – «нерівність трикутника».

У загальному|спільному| випадку відстанню називають функцію, що задовольняє вищенаведеним умовам. Цим умовам, зокрема, задовольняє геометричну відстань між двома крапками|точками| (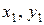) і (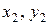) на площині|плоскості|: .

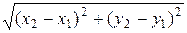За наявності 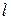біт можна побудувати|спорудити| 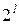кодових слів. Проте|однак| часто потрібні не всі з|із| цих слів. Якщо використовувати тільки|лише| частину|частку| кодових слів, то за допомогою перевірок на парність і інших прийомів можна виявити помилки і навіть їх виправляти|справляти|.

Припустимо|передбачимо|, що з|із| 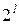використовуються тільки|лише| 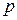слів: 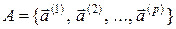. Якщо ці слова такі, що при всіх :

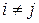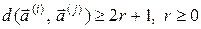, (7.1)

то можна виправляти|справляти| будь-які помилки кратності .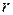

Допустимо, що в деяких 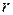компонентах слова при передачі виникли помилки, в результаті|унаслідок,внаслідок| яких символи 0 були прийняті як 1, а символи 1 – як 0 (помилки типу заміщення). Слово 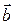, що вийшло в результаті, знаходиться|перебуває| на відстані 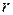від слова 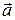. Отже, якщо вважати|лічити|, що помилки при передачі можуть виникати не більше ніж в 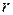компонентах, то сукупність всіх слів, які можуть вийти з 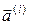|із|, є множина|безліч| .

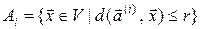З|із| нерівності трикутника і умови (7.1) виходить 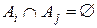, якщо тільки|лише| 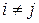. Дійсно, допустимо, що існує слово 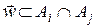. Тоді і .

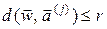Згідно нерівності трикутника

,

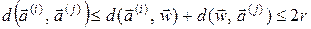що приводить|призводить,наводить| до суперечності|протиріччя| з|із| умовою (7.1).

Множина|безліч| 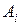називається областю декодування для слова 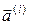. Оскільки|тому що| області декодування не перетинаються, то при прийомі слова з|із| області декодування 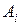можна вважати|лічити|, що передавалося слово 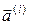. Якщо при цьому число помилок не перевершує, то при прийомі завжди ухвалюватиметься правильне рішення.

Оскільки|тому що| число елементів 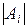в множині|безлічі| 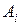рівне числу способів вибору деяких (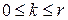) компонент слова 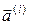, то

.

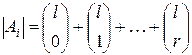Далі, оскільки 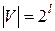|тому що|, то: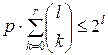, тобто|цебто|

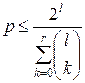. (7.2)

Нерівність (7.2) називається межею|кордоном| Хеммінга. Воно дає оцінку зверху для числа 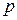кодових слів, які можна використовувати для передачі, якщо їх довжина рівна 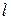біт і потрібно виправляти|справляти| всі 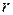- кратні помилки.

Приклад|зразок| 7.5.Хай|нехай| 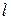=8, тоді 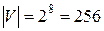. Оскільки 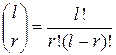, то ; ; ; ; .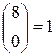

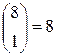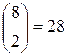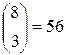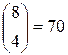Якщо 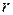=4, то .

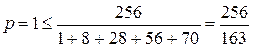Якщо 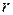=3, то .

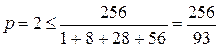Якщо 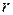=2, то .

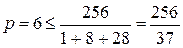Якщо 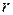=1, то .

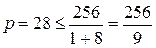Якщо 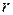=0, то .

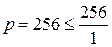Таким чином, якщо зустрічаються тільки|лише| одиночні помилки типу заміщення, то при використанні 8 біт можна безпомилково передавати 28 слів. У загальному|спільному| випадку, якщо є|наявний| 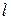біт і потрібно виправляти|справляти| одиночні помилки типу заміщення, то межа|кордон| Хеммінга визначається наступним|слідуючим| виразом|вираженням|, який є приватним випадком формули|з'являється,являється| (7.2):

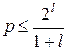. (7.3)

Позначимо мінімальне число біт, необхідне для передачі 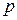слів, буквою|літерою| 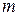. Тоді: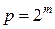, і з|із| формули (7.3) виходить

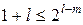. (7.4)

Таким чином, для перешкодостійкого кодування сигналів при одиночних помилках типу заміщення необхідно використовувати додаткові 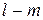біт, кількість яких повинна задовольняти умові (7.4). Даний випадок простий, але|та| одночасно практично дуже важливий|поважний|. Такою властивістю, як правило, володіють внутрішні шини передачі даних в сучасних комп'ютерах.

Приклад|зразок| 7.6.Для повідомлення|сполучення| завдовжки 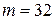буде потрібно 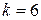додаткових розрядів, оскільки 64=.

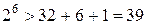Код, в якому використовуються додаткові розряди для перешкодостійкої передачі сигналів, називається кодом Хеммінга.

Читайте також:

1. Автоматичне кодування.
2. Алфавітне кодування
3. Аудит розрахунків за відшкодуванням завданих збитків
4. Бюджетне відшкодування ПДВ
5. Види зобов’язань з відшкодування шкоди, що виникають незалежно від вини заподіювача шкоди
6. Вимоги до методів цифрового кодування
7. Відшкодування збитків - це відновлення майнового стану учас­ника господарських правовідносин за рахунок іншого суб'єкта — правопорушника.
8. Відшкодування збитків постраждалим.
9. Відшкодування збитків як вид господарсько-правової відповідальності: поняття, сфера застосування, порядок реєстрації.
10. Відшкодування збитку, завданого з вини працівника
11. Відшкодування моральної шкоди
12. Відшкодування шкоди

Переглядів: 1457