• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Факторизація дробово-раціональної ФКЗ

Як відомо, дробово-раціональна функція комплексного аргументу вигляду

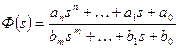(3.1)

має n нулів та m полюсів. В загальному випадку нулі та полюси є комплексними числами, тому функції типу (3.1) можна представити на комплексній площині у вигляді двох множин крапок: нулів – 0 та полюсів - ´, як представлено на рис. 3.1.

Рис. 3.1 Карта особливостей дробово-раціональної функції

За визначенням нуля та полюса можна записати дробово-раціональну функція, яка відповідає карті на рис. 3.1 як

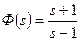. (3.2)

Нуль або полюс, розташований у лівій півплощині (ЛПП) комплексної площини називають стійким, оскільки він має від’ємну дійсну частину. Якщо нуль або полюс функції знаходиться у правій півплощині (ППП), то він є нестійким і має додатну дійсну частину.

Якщо дробово-раціональна функція не має полюсів або нулів у ППП, то її називають аналітичною у правій півплощині. В разі, коли усі особливості дробово-раціональної функції знаходяться у ППП, то її називають аналітичною у ЛПП.

Якщо нулі та полюси ФКЗ розташовані симетрично відносно уявної вісі, то така функція є парною та може бути додатно визначеною. Процедура (операція) факторизації полягає у тому, щоб вихідну додатно визначену парну дробово-раціональну ФКЗ Ф(s) представити у вигляді добутку двох комплексно спряжених функцій (факторів) F(s) та F_*(s)

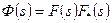(3.3)

таких, що F(s) є аналітичною у ППП ФКЗ.

Для пошуку фактору F(s) існує декілька методів []. Один з них, викладений в роботі [Ньютон], передбачає виконання наступних операцій.

1) представити вихідну ФКЗ у вигляді відношення приведених поліномів

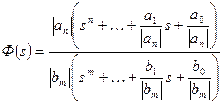; (3.4)

2) знайти нулі ФКЗ (3.4) s_i⁰ в результаті розв’язання алгебраїчного рівняння

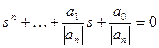; (3.5)

3) знайти полюси ФКЗ (3.4) s_i^p в результаті розв’язання алгебраїчного рівняння

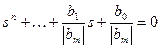; (3.6)

4) з усієї множини нулів s_i⁰ i=1,n та полюсів s_i^p i=1,m ФКЗ виділити лише ті, що мають від’ємну дійсну частину. Таких нулів повинно бути n/2, а полюсів – m/2;

5) визначити фактор F(s) за формулою

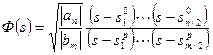. (3.7)

Приклад 3.1

Припустимо задана функція

.

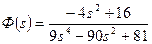Необхідно виконати факторизацію.

У відповідності з визначеним алгоритмом представимо вихідну функцію у вигляді відношення приведених поліномів

.

Знайдемо нулі отриманої функції

, , .

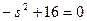Знайдемо полюси отриманої функції

. (3.8)

Для цього представимо ліву частину останнього рівняння у вигляді добутку двох комплексно спряжених поліномів, беручи до уваги те, що s=jω

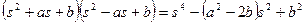. (3.9)

Порівняння коефіцієнтів при однакових степенях аргументу s дає можливість визначити, що

,

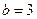в той час як

.

В такому разі рівняння (3.8) еквівалентне рівнянню

,

корені якого знаходять за відомою формулою знаходження коренів квадратного рівняння

, , , .

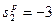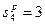Враховуючи лише нулі та полюси з від’ємною дійсною частиною можна записати результат факторизації у вигляді

.

Для перевірки правильності результату факторизації знайдемо комплексно спряжений до F(s) фактор F_*(s)

.

Добуток двох комплексно спряжених факторів F(s) та F_*(s) дорівнює вихідній матриці Ф(s). Таким чином, факторизація виконана правильно.

Читайте також:

1. Агрегування та факторизація
2. Модуль та аргумент дробово-раціональної ФКЗ
3. Сепарація дробово-раціональної ФКЗ
4. Факторизація

Переглядів: 438