• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Сепарація дробово-раціональної ФКЗ

Сепарацією(розщепленням) дробово-раціональної ФКЗ вигляду (3.1) називають її представлення у вигляді суми трьох ФКЗ

, (3.10)

де K₀ - поліном-результат ділення поліномів чисельників з Ф на відповідні поліноми знаменники, K₊, K_-- правильні дроби з полюсами, зосередженими у ЛПП і ППП комплексної змінної відповідно. Якщо прийняти до уваги визначення операції сепарації дробово-раціональної функції комплексного аргументу, наведене, наприклад, у [146], то пошук представлення (3.10) зводиться до виконання наступних операцій: ділення полінома-чисельника Ф на поліном знаменник та формування поліному частки K₀ і залишку K – правильний дріб, а також представлення результату K у вигляді суми правильних дробів, що мають тільки стійки та тільки нестійки полюси, та формування з них K₊ і K_- так, щоб виконувалася умова

. (3.11)

Як показано у джерелах [196, 213, 89, 215] існує декілька методів пошуку представлення (3.11). Одним з таких методів є метод невідомих коефіцієнтів [Коган]. Він передбачає виконання наступних операцій:

1) представити вихідну ФКЗ K у вигляді відношення приведених поліномів

; (3.12)

2) знайти полюси ФКЗ (3.12) в результаті розв’язання наступного рівняння

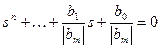; (3.13)

3) усю множину полісюв поділити на дві частини: підмножину стійких полюсів з кількістю елементів m₁ та підмножину нестійких полюсів m₂. До множини стійких полюсів P включити полюси s_i^p, які мають відємну дійсну частину. До множини нестійких полюсів N включити полюси s_i^p, які мають додатну дійсну частину.

4) На основі множин P і N знайти поліноми-знаменники з дробовораціональних функцій K₊ та K_-

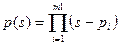; ; (3.14)

та скласти елементарні дробі

; (3.15)

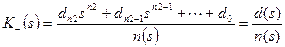; (3.16)

де n1=m1-1; n2=m2-1, а коефіцієнти c_i та d_j поліномів-чисельників є поки що невідомими;

5) Представити вираз (3.12) у вигляді

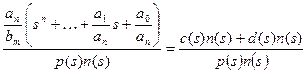; (3.17)

6) Визначити невідомі коефіцієнти поліномів c(s) та d(s) шляхом складання системи алгебраичних рівнянь на основі порівняння коефіцієнтів поліномів-чисельників виразу (3.17);

7) Підставити отримані значення відповідних коефіцієнтів c_i та d_j до формул (3.15), (3.16).

Приклад 3.2

Припустимо задано вихідну ФКЗ у вигляді

. (3.18)

Необхідно здіснити сепарацію.

У відповідності з наведеним алгоритмом спочатку необхідно знайти частку від ділення поліному-чисельника виразу (3.18) на поліном знаменник

.

Отже знадено частку K₀ та правильний дріб K у вигляді

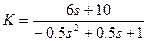; . (3.19)

Після цього необхідно представити ФКЗ K у вигляді відношення приведених поліномів (3.12)

. (3.20)

На другому етапі сепарації необхідно знайти полюси ФКЗ (3.20). Для досягнення цієї мети необхідно розвязати квадратне рівняння

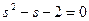. (3.21)

Розв’язок рівняння (3.21) має наступний вигляд

(3.22)

або

; . (3.23)

Знайдені таким чином корені (3.23) дозволяють визначити множини стійких Р та нестійких N полюсів які містять по одному елементу

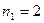, . (3.24)

Прийнявши до уваги вигляд множин P та N та скориставшись формулами з (3.18), знайдемо, що

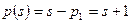; (3.25)

. (3.26)

Отже, структура результатів сепарації має наступний вигляд

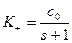, . (3.27)

Підстановка залежностей (3.25), (3.26) до формули (3.17) дозволила записати наступне рівняння

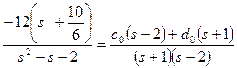
або після перетворень

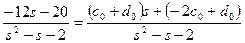. (3.28)

Порівняння чисельників з виразу (3.28) дозволяє скласти наступну систему лінійних алгебраічних рівнянь для визначення невідомих коефіцієнтів c₀ та d₀

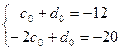. (3.29)

Розвязок цієї системи методом визначників має наступний вигляд

;

;

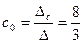де

;

;

.

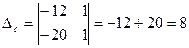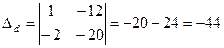Підстановка отриманих таким чином значень коефіцієнтів c₀ та d₀ дозволила знайти наступний результат сепарації

; (3.30)

. (3.31)

Для перевірки точності знаходження результатів (3.31), (3.32) знайдена сума

. (3.32)

Порівняння результату (3.32) з виразом (3.20) доводить коректність результату.

Таким чином, описано алгоритм рішення задачі сепарації дробово-раціональної матриці K, який дозволяє з високою точністю знаходити результати.

Читайте також:

1. Модуль та аргумент дробово-раціональної ФКЗ
2. Сепарація вторинної пари
3. Факторизація дробово-раціональної ФКЗ
4. Що таке сепарація палива?

Переглядів: 492