• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Просторові криві лінії

Як вже відомо, точки просторової кривої не належать одній площині. Для аналізу просторової кривої використовують так званий просторовий тріедр, або тригранникФрене,рис. 10. На цьому рисунку зображено відрізок просторової кривої AB та його горизонтальна проекція A₁B₁. Точку C відрізка кривої суміщено з початком координат. Уявімо тепер дві точки на кривій, що лежать по обидві боки від точки C. Як відомо, через три точки можна провести єдину площину. Нехай ці точки прямують до точки C з обох боків. Тоді в граничному положенні, коли ці точки будуть нескінченно близькими до точки C, через них пройде площина S, що найбільш щільно прилягає до кривої в точці C. Таку площину називають стичною, в ній лежать як дотична до плоскої кривої t, так і головна нормаль до неї n₁. У диференціальній геометрії доведено, що крива в околі точки стику лежить по обидва боки від стичної площини. Вертикальну площину L, перпендикулярну до стичної площини, що проходить через нормаль n₁, називають нормальною. У цій площині лежить як головна нормальn₁, так і бінормаль n₂, перпендикулярна в точці C до стичної площини. Третю площину G, перпендикулярну до перших двох, називають спрямною. Вона визначається дотичноюt та бінормаллю n₂.

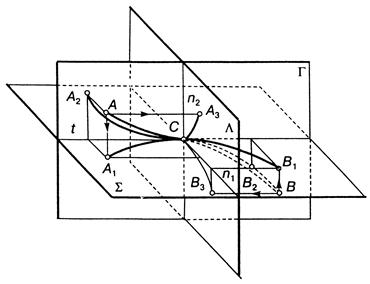
Рис. 10

В кожній точці просторової кривої (за винятком деяких особливих точок) можна провести єдину дотичну, як і до плоскої кривої. Просторові криві лінії визначаються кількістю параметрів п+6, де п – кількість параметрів форми, яке у різних кривих різне.

Читайте також:

1. Бюджетні множини й лінії бюджетного обмеження
2. Вибір індикатора . Криві титрування
3. Визначення довжини лінії
4. Вимірювання дирекційного кута лінії MN
5. Вплив радіостанцій на лінії зв'язку
6. Головні лінії площини
7. До комунікаційних споруд відносяться системи тепло -, водо -, електро - забезпечення, лінії зв’язку, очисні споруди. Вони можуть бути підземні, наземні та повітряні.
8. ДОСЛІДЖЕННЯ ЛІНІЇ ПЕРЕДАЧІ ЕЛЕКТРИЧНОЇ
9. За рівнем механізації процесів розрізняють автоматичні і напівавтоматичні потокові лінії.
10. За характером переміщення розрізняють конвеєрні лінії з безперервним та пульсуючим рухом.
11. За ціною для окремої точки на кривій
12. За ціною для окремої точки на кривій

Переглядів: 1079