• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Етапи підготовки наукового експерименту

Для проведення будь-якого виду експерименту необхідно попередньо спланувати та виконати таке:

- розробити гіпотезу, яка підлягає перевірці, та методику експериментальних робіт;

- визначити способи і прийоми впливу на об'єкт дослідження;

- забезпечити умови для виконання експериментальних робіт;

-розробити шляхи і прийоми фіксування ходу і результатів експерименту;

- підготувати засоби експерименту (прилади, установки, моделі тощо);

- забезпечити експеримент необхідним обслуговуванням.

Особливе значення має правильне розроблення методики експерименту.

Методика— це сукупність обдуманих і фізичних операцій, які розміщені у визначеній послідовності для досягнення поставленої мети дослідження.

Під час розроблення методики проведення експерименту необхідно
передбачити:

- попереднє цілеспрямоване спостереження за об'єктом або явищем, що вивчається, з метою визначення вихідних даних (гіпотез, обрання змінних факторів);

- створення умов, у яких можливе експериментування (добір об'єктів для експериментальної дії, усунення впливу випадкових факторів);

- визначення області інтересу для змінних факторів та меле вимірювання;

- можливість систематичного спостереження за розвитком явища і точного опису фактів;

- проведення систематичної регістрації замірів і оцінок фактів різними засобами і способами;

- створення складних ситуацій з метою підтвердження або спростування раніше отриманих даних;

- перехід від емпіричного вивчення з логічним узагальненням до аналізу та теоретичного оброблення отриманих фактичних даних.

Обравши методику експерименту, дослідник повинен переконатись у можливості її практичного застосування. Це необхідно зробити навіть у тому випадку, якщо методика раніше апробована в інших лабораторіях, оскільки вона може бути неприйнятною або складною в силу специфічних особливостей клімату, приміщення, лабораторного обладнання, персоналу, об'єкта дослідження тощо.

Перед кожним експериментом складається його план (програма виконання), який включає такі етапи:

- мету, задачі та обґрунтування об'єму експерименту;

- вибір змінних факторів;

- визначення кількості дослідів та послідовності зміни факторів;

- вибір кроку зміни факторів, визначення інтервалів між майбутніми експериментальними точками;

- обґрунтування вибору засобів для вимірювання;

- опис проведення експерименту;

- обґрунтування вибору способів оброблення та аналізу результатів
експерименту.

Необхідно також обґрунтувати вибір засобів вимірювання приладів та іншого обладнання (машин і апаратів). У зв'язку з цим експериментатор повинен бути добре обізнаний з існуючою вимірювальною апаратурою в Україні і за кордоном. Звичайно, в першу чергу необхідно використовувати стандартні машини і прилади, які випускаються серійно, робота на яких регламентується інструкціями, стандартами та іншими офіційними документами. Але в окремих випадках виникає потреба у створенні унікальних приладів, установок, машин для виконання досліджень. Тоді розроблення і конструювання приладів та інших засобів повинно бути ретельно обґрунтовано теоретичними розрахунками і практичними міркуваннями щодо можливості їх виготовлення.

Для створення нових приладів доцільно використовувати готові вузли, які випускаються промисловістю приладобудування, або ж реконструювати існуючі прилади. Відповідальним моментом у підготовці засобів вимірювання є визначення точності виміру і похибки.

Методи вимірюваньповинні базуватися на законах спеціальної науки метрології, яка вивчає вимірювальні засоби і методи.

Методи вимірювань можна розділити на прямі й не прямі. Під час прямих вимірювань шукану величину знаходять із досліду, а під час непрямих — за функціональними вимірами. Наприклад, b=f(а), де b — величина, яка знайдена за допомогою непрямих вимірів.

Вимірювання бувають абсолютні й відносні. Абсолютні — це прямі заміри в одиницях вимірювальної величини; відносні заміри — це відношення вимірюваної величини до одноіменної величини, яка приймається за вихідну одиницю. Наприклад, вологість сипучого корму приймається у відносних одиницях (відсотках) щодо повного її водонасичення.

Необхідно виділити декілька основних способів вимірювань.

Спосіб безпосередньої оцінки — відповідає визначенню величини безпосередньо за відліковим пристроєм вимірювального приладу прямої дії. Наприклад, вимірювання маси на електронних вагах.

Спосіб порівняння — передбачає необхідну вимірювальну величину порівнювати з величиною, що є мірою. Наприклад, вимірювання маси на важільних вагах із урівноваженням гирями.

Спосіб протиставлення — здійснюється шляхом порівняння з мірою, тобто вимірювана величина і величина, що є мірою, одночасно діють на пристрій, за допомогою якого встановлюється співвідношення між цими величинами. Наприклад, під час вимірювання маси на рівноплечих вагах із встановленням вимірюваної маси і гир на обидвох протилежних чашах ваг.

Диференційний спосіб — полягає в тому, що на вимірний пристрій діє різниця виміряної та відомої величини, яка є мірою. Наприклад, виміри, що виконуються під час перевірки мір довжини порівнянням із мірним зразком.

Нульовий спосіб — полягає у доведенні результату ефективної дії величини на пристрій до нуля. Наприклад, вимірювання електричного опору через міст шляхом повного його зрівноваження.

Спосіб заміщення — передбачає заміну вимірюваної величини відомою величиною з відновлюваною мірою. Наприклад, зважування з почерговим ставленням вимірюваної маси і гирі на одну й ту саму шальку.

Спосіб збігу полягає в тому, що різниця між заданою величиною і величиною, яка є мірою, визначається шляхом збігу відміток шкал або періодичних сигналів.

Наведені способи вимірювань знаходять широке застосування під час експериментальних досліджень, що відбуваються в галузі механізації тваринництва.

6.4.3 Сутність класичного планування експерименту

Вибір плану експерименту значною мірою залежить від об'єму початкової інформації про досліджуваний об'єкт. Така інформація може бути отримана після вивчення першоджерел у вигляді результатів експериментальних досліджень у суміжних з аналогічними об'єками областях та у вигляді отриманих раніше теоретичних досліджень.

В умовах достатньо повної інформації метою експериментального дослідження може бути підтвердження теоретичних розрахунків, знаходження експериментальних коефіцієнтів для рівнянь або пошук оптимального рішення. Число дослідів визначається характером залежностей, які описують певний процес. Якщо, наприклад, залежність вихідного параметра від вхідного фактора має лінійний характер, то для визначення коефіцієнтів рівняння достатньо провести два досліди. В умовах достатньої інформації про об'єкт дослідження кількість змінних факторів та їх інтервали можна визначити залежно від мети досліду.

В умовах неповної або суперечливої інформації, коли відома тільки область експерименту, необхідно визначити характер залежностей, які пов'язують фактори з вихідним параметром. У цьому випадку значення факторів інтуїтивно розбивають на інтервали з отриманням певної кількості рівнів для кожного фактора, а потім, під час проведення експерименту, реалізують усі можливі сполучення рівнів факторів.

В умовах відсутності апріорної інформації про об'єкт дослідження невідомими є як область експерименту, так і фактори. У цьому випадку дослід планують за ходом експерименту. Отримавши і проаналізувавши результат першого досліду, дослідник планує наступний. Потім в експеримент залучаються нові змінні фактори, і впродовж усього експерименту дослідник отримує нову інформацію про об'єкт дослідження і процеси, які в ньому відбуваються.

План експерименту може бути складений у формі планово-контрольної карти і методичної сітки або матриці. У планово-контрольну карту почергово вносять усі змінні фактори та їх рівні, що дає змогу наочно відтворити область експерименту, кількість і послідовність дослідів. При складанні планово-контрольної карти рівні факторів позначають цифрами.

Методичну план-матрицю дослідів розробляють у вигляді таблиці, в якій додатково передбачено результати трьох паралельних дослідів.

Успішне виконання дослідів, економічність їх проведення, точність і надійність результатів залежать від ретельної підготовки до експерименту: розроблення експериментальної установки, вибір вимірювальних приладів, виготовлення зразків.

Під час проведення експерименту необхідно враховувати фактор часу. Досліди потрібно виконати в найкоротші терміни, щоб не допустити вимушених змін властивостей матеріалу зразків, зносу експериментальної установки, зміни зовнішніх умов проведення дослідів.

Експериментальна установка повинна забезпечувати досліди на реальних зразках, тому що внесення масштабного фактора спотворює результати дослідів і їх необхідно перевіряти у виробничих умовах.

6.4.4 Сутність математичного планування експерименту та обробки результатів

Планування експерименту — це вибір числа та умов проведення дослідів, необхідних і достатніх для розв'язання поставленого завдання зі заданою точністю.

Під час дослідження процесів машин для тваринництва в більшості випадків на об'єкт дослідження одночасно діє декілька змінних факторів, що відповідає умовам багатофакторного експерименту. У разі наявності останнього можливі два методи планування експерименту:

- класичний метод, за яким досліджується вплив на об'єкт кожного фактора окремо, змінюючи його значення та фіксуючи решту факторів на сталому рівні;

- математичний метод, що дозволяє досліджувати вплив на об'єкт одночасно всіх факторів, змінюючи їх рівні за відповідним, наперед розробленим, планом.

У практиці планування експериментальних досліджень використовуються обидва методи, але другий має низку переваг, а саме:

- значно зменшується необхідна кількість дослідів за наявності великої кількості змінних факторів;

- математичний опис процесу здійснюється у вигляді єдиного рівняння, яке включає всі змінні фактори, тоді як при першому методі кількість рівнянь, що описують процес, дорівнює кількості змінних факторів.

Основним завданням математичного планування експерименту є розроблення багатофакторних планів, котрі забезпечували б можливість отримати достатньо точну модель процесу у вигляді одного рівняння з мінімальної кількості дослідів.

Під час планування експерименту можуть вирішуватись такі задачі:

- інтерполяційна, метою якої є побудова поверхні відгуку в факторному просторі для з'ясування характеру впливу кожного фактора на функцію відгуку;

- оптимізаційна, метою якої є визначення найкращого поєднання значень факторів, що забезпечує оптимальне значення функції відгуку.

Рівняння, яке встановлює зв'язок між значенням функції відгуку (вихідної величини) та значеннями змінних факторів, називають математичною моделлю процесу дослідження.

Якщо на об'єкт дослідження діють змінні фактори, що позначаються Х₁, X_2, ... X_і, які визначають його стан у якості вихідного параметра Y, то математичною моделлю процесу називають функцію у вигляді Y=f(X_1, X_2, …X_i).

Обрати модель —означає знайти вигляд функції, записати її рівняння, яке називають рівнянням регресії.

Наприклад, рівняння регресії для двох змінних факторів може бути записано у вигляді:

- лінійного рівняння:

; (6.1)

- неповного квадратного рівняння:

; (6.2)

- рівняння другого порядку:

; (6.3)

де b₀, b₁, b₂, b₁₂, b₁₁, b₂₂ — коефіцієнти рівнянь регресії.

Здебільшого під час дослідження технологічних процесів машин для тваринництва зв'язок між факторами та вихідним параметром достатньою мірою можна описати рівняннями другого порядку. Для отримання лінійного або неповного квадратного рівняння застосовують плани першого порядку, а для отримання моделі у вигляді квадратного рівняння — план другого порядку.

Для вибору напрямку та умов експерименту, перш за все, необхідно з'ясувати кількість змінних факторів та визначити інтервали їх варіювання. Ця процедура є досить важливим етапом наукового дослідження. Вона вирішується на основі всебічного вивчення явища, що досліджується, літературних джерел, проведення теоретичного аналізу, практичного досвіду й у кожному випадку носить творчий та індивідуальний характер. Після прийняття рішення про вихідний параметр та змінні фактори, вплив яких передбачається досліджувати, а також про область зміни значень кожного виконують кодування факторів.

Заміна натуральних значень факторів у відповідних одиницях виміру безрозмірними кодовими значеннями спрощує план експерименту та процес статистичного оброблення експериментальних даних. Кожному фактору присвоюють, у тій самій послідовності, що й натуральним, кодове значення Х₁, Х₂тощо. Найбільше кодове значення кожного фактора позначають (+1) та називають його верхнім рівнем, а найменше значення позначають (-1) і називають нижнім рівнем. Середнє значення позначають (0): це основний рівень.

Для факторів із безперервною областю визначення зв'язок між кодовим і натуральним значенням визначають за формулою:

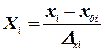, (6.4)

де X_і— кодове значення фактора;

х_і— натуральне значення фактора;

х_0і— натуральне значення середнього рівня;

∆_хі інтервал зміни фактора, що визначається як половина різниці між натуральними значеннями верхнього та нижнього рівнів фактора.

Під час складання плану експерименту та оброблення експериментальних даних усі фактори, незалежно від їх фізичної суті та числових значень, будуть мати однакові кодові значення (+1, 0, -1). Розшифрування, тобто перехід до натуральних значень факторів, виконується після закінчення статистичного оброблення даних.

У планах першого порядку використовують тільки верхній та нижній рівні факторів. У планах другого порядку, крім зазначених, послуговуються й іншими рівнями, методика визначення та кодування яких наведена нижче.

Повним факторним планом (ПФП) називають план, в якому реалізуються всі можливі сполучення двох рівнів факторів (верхнього та нижнього). Кількість дослідів у цьому випадку визначають за формулою N=2^К, де к – кількість змінних факторів. Якщо досліджується вплив двох змінних факторів, то N=2²=4.

Для побудови матриці ПФП потрібно перейти до безрозмірних нормалізованих (кодових) позначень змінних факторів (згідно з формулою 6.4). Запровадження нормалізованих значень факторів створює ряд переваг. Незалежно від фізичної суті та діапазону зміни фактора його нижній рівень у нормалізованих позначеннях дорівнює (-1), верхній рівень — (+1), а основний рівень — (0). Тому матрицю ПФП у нормалізованих позначеннях можна будувати перебором рівнів (-1) і (+1), нехтуючи конкретними діапазонами зміни кожного з факторів.

Основними характерними властивостями план-матриць у кодових значеннях, які визначають точність результатів та сфери застосування відповідних планів для побудови математичних моделей, є: симетричність, нормованість, ортогональність, рототабельність, уніформність, композиційність.

Симетричнимивідносно центра експерименту називають плани, для яких сума чисел будь-якого стовпця дорівнює нулю, тобто:

(для будь-якого j). (6.5)

Нормованиминазивають плани, для яких сума квадратів елементів кожного стовпця дорівнює числу дослідів, тобто:

. (6.6)

Ортогональниминазивають плани, для яких сума почленних добутків будь-яких двох стовпців матриці дорівнює нулю:

(для j ≠ u=1…k). (6.7)

Властивість ортогональності дозволяє значно спростити процес визначення коефіцієнтів рівняння регресії, яке має загальний вигляд:

, (6.8)

де X_j , Х_и— лінійні значення факторів; b₀, b_j, b_ju, b_jj— коефі­цієнти членів рівняння; Х_jХ_и — взаємодія двох різних факторів плану.

Рототабельністьплану забезпечує однакову точність поверхні відгуку, незалежно від напрямку руху від центра експерименту до будь-яких рівновіддалених точок.

Уніформністьпланів забезпечує сталість дисперсії в деякій області навколо центра експерименту.

Композиційніплани дозволяють проводити експеримент частинами, тобто, в разі необхідності, переходити до планування більш високого порядку, зберігаючи одночасно результати попередніх дослідів.

Зазначимо, що ПФП відповідають вищенаведеним властивостям. Для надання потрібних властивостей планам другого порядку варто користуватись спеціальними прийомами, про що йтиметься нижче.

Методика обробки результатів експерименту включає в себе такі основні етапи:

- визначення відновлюваності результатів рівняння регресії;

- розрахунок і оцінка значущості коефіцієнтів рівняння регресії;

- визначення рівня відповідності одержаної математичної моделі експериментальним даним, тобто перевірка адекватності рівняння регресії.

Визначення відновлюваності результатів дослідів. З метою забезпечення достовірності одержаних результатів, під час реалізації плану експерименту в кожному досліді (за однакових умов), виконують декілька спостережень. Кількість спостережень визначається залежно від надійності дослідів. Під дією некерованих і невідомих факторів числове значення вихідного параметра при повторенні досліду відрізняється одне від одного. Тому для кожного досліду визначають середнє значення _i, і дисперсію .

Відновлюваність досліду перевіряється за критерієм Кохрена (G_p):

, (6.9)

де 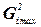— найбільша за числовим значенням дисперсія одного з дослідів, яка визначається (як і всі інші дисперсії дослідів) за формулою:

, (6.10)

де n — кількість повторень (дублювань) кожного досліду;

y_ij— значення вихідної величини в j-му дублюванні і-го досліду
(j=1...n, і=1...N);

— середнє значення вихідної величини в i-му досліді;

G(q, f_y , f_n) — табличне значення критерію Кохрена, яке обирається за статистичними таблицями залежно від: q — рівня достовірності (у більшості випадків q=0,05);

f_y — кількості незалежних значень дисперсії, f_y=N; f_n=п-1— числа свободи кожного значення, де п— кількість дублювань корисного досліду.

Умова G_p≤G_табл означає, що коли розрахункове значення критерію Кохрена буде менше або дорівнюватиме табличному, то різниця між значеннями спостережень перебуватиме в межах необхідної точності досліду.

Невиконання цієї умови означає, що на об'єкт дослідження впливають невраховані фактори, або значення фактора, що прийнято за стале, в дійсності змінюється. У цьому випадку необхідно ще раз детально проаналізувати умови проведення експерименту.

Після такої оцінки визначається дисперсія відновлюваності досліду(помилка досліду) за формулою:

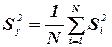(6.11)

Розрахунок і оцінка коефіцієнтів рівняння регресії.

Спочатку визначається вільний член рівняння за фор­мулою:

, (6.12)

де — середнє арифметичне значення параметра оцінки кожного досліду.

Коефіцієнти інших членів рівняння регресії (6.8) визначають за такими формулами:

- коефіцієнти біля кожного фактора:

, для (j=1, 2…K), (6.13)

де X_ji— кодове значення j-го фактора в і-му досліді ПФП;

- коефіцієнти біля взаємодій факторів

, для (j ≠ , u = 1, 2…n). (6.14)

Числові значення розрахованих коефіцієнтів рівняння регресії показують величину впливу того чи іншого фактора або взаємодії факторів на вихідний параметр.

Серед визначених коефіцієнтів можуть бути такі, що за своєю величиною не мають значного впливу на вихідний параметр. Тому для спрощення рівняння регресії ними можна знехтувати, попередньо з'ясувавши величину їх значущості.

Оцінка значущості коефіцієнтіввиконується за допомогою критерію Стьюдента. Коефіцієнт вважають значущим, якщо виконується нерівність:

, (6.15)

де ∆b — похибка коефіцієнта, яка визначається за формулою:

, (6.16)

t_qf — табличне значення критерію Стьюдента, яке обирається за таблицями для відомих: q— рівень достовірності (q = 0,05);

f— кількість ступенів свободи дисперсії відновлення, яке дорівнює f = N(n-1).

Якщо за абсолютною величиною значення коефіцієнта менше за його похибку (6.15), то коефіцієнт уважають незначним, і відповідний член виключається із рівняння регресії.

Перевірка рівняння регресії на адекватністьозначає оцінку достатньої точності результатів, одержаних за рівнянням, порівняно з відповідними фактичними значеннями дослідів. Така перевірка здійснюється за допомогою критерію Фішера. Якщо рівняння адекватне, то виконується нерівність:

(0,05, f₁, f₂), (6.17)

де F_розр— розрахункове значення критерію Фішера, яке визначається за формулами:

, якщо ; (6.18)

, якщо , (6.19)

де S_ад — дисперсія адекватності, яка в свою чергу визначається за формулою:

, (6.20)

де f_ад — число ступенів свободи дисперсії адекватності f_ад = N - Р, де Р— число значущих коефіцієнтів рівняння регресії;

у_i— значення параметра оцінки для кожного досліду, розраховане за одержаним рівнянням регресії в кодових значеннях;

F_табл— табличне значення критерію Фішера, що обирається залежно від
f₁ = f_ад = N - Р– числа ступенів свободи дисперсії адекватності та f₂ = f_y = N(n-1) – числа ступенів свободи дисперсії відновлення.

Якщо умова адекватності виконується, то можна вважати, що результати рівняння регресії з достатньою точністю узгоджені з результатами дослідів, а якщо умова адекватності не виконується, то це лінійне рівняння недостатньо точно описує процес, що досліджується, і тоді приймають одне із таких рішень:

- включають у модель нові взаємодії факторів;

- зменшують діапазон зміни факторів;

- переходять до планів другого порядку. Включення в модель усіх взаємодій факторів дає можливість одержувати більш точну характеристику їх впливу на об'єкт дослідження. Однак, для оцінки адекватності такої моделі не вистачає ступенів свободи у рівнянні (6.20). Так, двофакторна модель із взаємодією має чотири коефіцієнти для чотирьох дослідів, трифакторна модель – вісім коефіцієнтів для восьми дослідів. Тому доводиться нехтувати деякими взаємодіями, особливо більш високих порядків, або проводити додаткові досліди.

Cпосіб зменшення діапазону зміни факторів можна застосовувати лише в технічно обґрунтованих випадках. Тому найчастіше обирають рішення, яке передбачає перехід до плану другого порядку.

Маючи адекватне рівняння, можна прогнозувати всі можливі значення параметра оцінки процесу для будь-яких значень факторів, що знаходяться між верхнім і нижнім рівнями. Аналіз одержаного рівняння регресії полягає у визначенні відносної значущості кожного змінного фактора та їх взаємодій і поясненні фізичної суті цих явищ.

Краще за все виконувати аналіз, користуючись рівнянням регресії в кодових значеннях факторів, яке має такі загальні особливості:

- абсолютна величина лінійного коефіцієнта рівняння регресії свідчить про ступінь (величину) впливу відповідного фактора на вихідний параметр оцінки досліджуваного процесу; більший вплив має той фактор, числове значення коефіцієнта якого більше;

- знаки лінійних коефіцієнтів рівняння регресії несуть дуже важливу інформацію, а саме: якщо коефіцієнт додатний, то вихідна величина зростає зі збільшенням значення відповідного фактора та зменшується за його зменшення; для коефіцієнтів з від'ємним значенням ця залежність має зворотний характер;

- рівняння регресії дозволяє розрахувати значення вихідного параметра для будь-якої точки в області зміни факторів, тому на його основі можна будувати графічні залежності від одного з факторів при фіксованих значеннях інших або від двох, трьох факторів одразу, графіки яких відображаються в об'ємних координатах.

Результат багатофакторного експерименту графічно можна уявити у вигляді поверхні відгуку. Якщо всі фактори виявляють лінійний вплив на вихідну величину і процес описується рівнянням першого порядку, то поверхня відгуку буде мати плоску форму. Якщо ж процес описується рівнянням другого порядку, то поверхня набуває криволінійної формиі тим більш складної, чим більше факторів виявляють нелінійний характер впливу на величину параметра оцінки досліду.

Одержана математична модель може бути основою для оптимізації процесу, що досліджується, або раціонального керування ним.

Для одержання математичної моделі у натуральних значеннях факторів необхідно замінити кодові значення факторів на натуральні, використавши залежність (формула 6.4). Потрібно пам'ятати, що рівняння в натуральних значеннях втрачає важливу інформативність шодо аналізу результатів досліджень, яка характерна для нормалізованих моделей. Тому аналіз результатів досліджень виконують тільки за рівнянням регресії у кодових значеннях.

Читайте також:

1. III. Етапи розробки програмного забезпечення
2. IXX. ОСОБЛИВОСТІ ПРИЙОМУ ДО кафедри військової підготовки НАУ
3. VII. ОСНОВНІ ЕТАПИ РОЗВИТКУ УКРАЇНСЬКОЇ КУЛЬТУРИ У ХХ ст.
4. Асортиментний процес включає три основних етапи: концентрацію, кастомізацію і розсіювання.
5. Аудит фінансово-господарської діяльності бюджетних установ включає три етапи.
6. Базовий рівень підготовки.
7. Бізнес-моделювання в системі управління розвитком підприємства. Поняття та етапи формування бізнес-моделі
8. Бюджетний процес, його поняття і складові етапи
9. В межах наукового підходу існує велика кількість концепцій, але найбільш переконлива – еволюційна теорія.
10. В.О. Сухомлинський — майстер унікального експерименту
11. Вибір теми наукового дослідження
12. Виборчий процес і його етапи

Переглядів: 2175