• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Вплив зміни частоти синхронізуючого сигналу і частотно-залежного параметра на величину відхилення часових інтервалів

Обладнання екстремальної комп’ютерно-інтегрованої системи є частотно-залежними пристроями.

Вплив зміни частоти синхронізуючого сигналу на величину відхилення часових інтервалів можна пояснити неідеальністю характеристик обладнання екстремальної комп’ютерно-інтегрованої системи керування технологічними процесами обробки даних в цифрових телекомунікаційних мережах, наявністю статичної фазової помилки системи управління, цифровою обробкою сигналу управління в мікропроцесорі.

Дослідження впливу статистик зміни частоти синхронізуючого сигналу на величину відхилення часових інтервалів проводитимемо вважаючи, що відсутня дія інших дестабілізуючих фактів, так як це було зроблено в попередніх випадках. Тоді величину відхилення часових інтервалів можна представити як функцію двох змінних величин

(26)

де 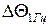– відхилення часових інтервалів при зміні частоти синхронізуючого сигналу на 1 Гц; Δƒ – зміна значення частоти синхронізуючого сигналу відносно вихідного значення при якому виконувалась настройка пристрою.

Таке представлення зручне тим, що випадкова величина розділяється на дві випадкові величини: 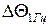– є випадковою величиною в умовах масового виробництва пристроїв; Δƒ – є випадковою величиною в умовах експлуатації пристроїв на телекомунікаційній мережі. Причому перший співмножник випадкової величини цілком визначається технічними властивостями пристроїв, другий, – умовами експлуатації. На підставі теореми про математичне очікування і дисперсію твору двох незалежних випадкових величин, отримаємо:

(27)

(28)

Визначимо статистики зміни частоти синхронізуючого сигналу 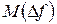і 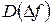. При цьому враховуватимемо, що межі зміни частоти синхронізуючого сигналу задані у вигляді максимально допустимих відхилень Δƒ_макс відносно номінального значення. Синхронізуючий сигнал для обладнання екстремальної комп’ютерно-інтегрованої системи можна отримати від атомних стандартів частоти, супутникових навігаційних систем GPS, ГЛОНАС, кварцових генераторів, що задають тактові частоти цифрових телекомунікаційних систем. В якості прикладу розглянемо випадок, коли синхронізуючий сигнал ПФ ПВЧ є тактовий синхросигнал цифрового потоку Е1 телекомунікаційних систем з номінальним значенням 2048 кГц.

Розподіл зміни частоти для досить показної вибіркової партії кварцових резонаторів підкорятиметься закону Гауса (див. рис.3). Граничні значення зміни тактової частоти цифрового потоку Е1 телекомунікаційних систем Δƒ_макс і Δƒ_мін визначаються стандартами.

Отже математичне очікування і дисперсія зміни значення частоти синхронізуючого сигналу будуть визначаться з рівнянь:

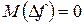(29)

(30)

Підставляючи вирази (29) і (30) відповідно в (27) і (28), отримаємо для загального випадку роботи однотипних пристроїв математичне очікування

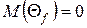(31)

і дисперсію величини відхилення часових інтервалів при зміні частоти синхронізуючого сигналу

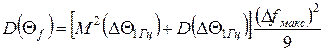(32)

Визначимо статистики частотно-залежного параметра 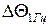- відхилення часових інтервалів при зміні частоти синхронізуючого сигналу на 1 Гц. Розподіл вірогідності окремих значень цього параметра підпорядковано закону Гауса (див. рис.3). Це пояснюється наявністю значної кількості окремих деталей (кварцовий резонатор, варикапи, індуктивності, ємності і т. д.), параметри яких визначають величину .

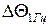З врахуванням цього можна записати, що математичне очікування відхилення часових інтервалів при зміні частоти синхронізуючого сигналу на 1 Гц рівно номінальному значенню

, (33)

а дисперсія визначатиметься з наступного рівняння з вірогідністю 0,997

, (34)

де 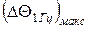- максимальне значення розкиду відхилення часових інтервалів при зміні частоти синхронізуючого сигналу на 1Гц.

Підставляючи (33) і (34) відповідно в (31) і (32) остаточно отримаємо для загального випадку математичне очікування і дисперсію величини відхилення часових інтервалів при зміні частоти синхронізуючого сигналу:

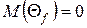(35)

. (36)

Читайте також:

1. I визначення впливу окремих факторів
2. I етап. Аналіз впливу типів ринку на цінову політику.
3. II. Фактори, що впливають на зарплату при зарубіжних призначеннях
4. IV. Критерій питомої потенціальної енергії деформації формозміни
5. Ne і ne – поточне значення потужності і частоти обертання колінчастого вала.
6. VI етап. Аналіз варіантів зміни цін конкурентами.
7. А — позитивна умовна реакція натискання на клавішу, В — бурхлива емоційно-рухова реакція за відсутності харчового підкріплення сигналу.
8. А. Без зміни хазяїна та ендогенної агломерації
9. А. Без зміни хазяїна та ендогенної агломерації
10. Адаптаційні зміни в кістковій системі спортсменів
11. Адаптаційні зміни суглобово-зв'язкового апарату спортсменів різних спеціалізацій.
12. АДАПТАЦІЯ ОПЕРАЦІЙНОЇ СИСТЕМИ ДО ЗМІНИ ЇЇ ЗАВАНТАЖЕННЯ.

Переглядів: 607