
РЕЗОЛЮЦІЯ: Громадського обговорення навчальної програми статевого виховання
ЧОМУ ФОНД ОЛЕНИ ПІНЧУК І МОЗ УКРАЇНИ ПРОПАГУЮТЬ "СЕКСУАЛЬНІ УРОКИ"
ЕКЗИСТЕНЦІЙНО-ПСИХОЛОГІЧНІ ОСНОВИ ПОРУШЕННЯ СТАТЕВОЇ ІДЕНТИЧНОСТІ ПІДЛІТКІВ
Батьківський, громадянський рух в Україні закликає МОН зупинити тотальну сексуалізацію дітей і підлітків
Відкрите звернення Міністру освіти й науки України - Гриневич Лілії Михайлівні
Представництво українського жіноцтва в ООН: низький рівень культури спілкування в соціальних мережах
Гендерна антидискримінаційна експертиза може зробити нас моральними рабами
ЛІВИЙ МАРКСИЗМ У НОВИХ ПІДРУЧНИКАХ ДЛЯ ШКОЛЯРІВ
ВІДКРИТА ЗАЯВА на підтримку позиції Ганни Турчинової та права кожної людини на свободу думки, світогляду та вираження поглядів
- Гідрологія і Гідрометрія
- Господарське право
- Економіка будівництва
- Економіка природокористування
- Економічна теорія
- Земельне право
- Історія України
- Кримінально виконавче право
- Медична радіологія
- Методи аналізу
- Міжнародне приватне право
- Міжнародний маркетинг
- Основи екології
- Предмет Політологія
- Соціальне страхування
- Технічні засоби організації дорожнього руху
- Товарознавство продовольчих товарів
Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция
За своєю електропровідністю плазма наближається до провідників.
Плазму необхідно вважати четвертим агрегатним станом речовини.
НАЙВАЖЛИВІШІ ВЛАСТИВОСТІ ПЛАЗМИ:
3. Сильна взаємодія з зовнішніми магнітними та електричними полями.
4. Специфічна колективна взаємодія частинок плазми, що здійснюється через особливе поле.
5. Плазма є своєрідним пружним середовищем, у якому легко збуджуються і розповсюджуються різного роду коливання та хвилі.
Розрізняють “низькотемпературну плазму” (Тіон£105К) та “високотемпературну плазму” – Тіон~106…108К.
Лекція №15
IV. ЕЛЕКТРОМАГНЕТИЗМ
30. Магнітне поле. Магнітна індукція.
Закон Ампера
Досліди показали, що навколо провідників зі струмом і постійних магнітів існує магнітне поле, яке легко виявити за силовою дією, якою воно впливає на інші провідники зі струмом або постійні магніти.
Щоб вивчити основні властивості магнітного поля і способи його створення, розглянемо два досліди.
1. Взаємодія між нерухомими електричними
зарядами і магнітною стрілкою
Підвісимо на нитці коло магнітної стрілки кульку з діелектрика і надамо їй електричного заряду. Ми не помітимо будь-якої дії з боку нерухомих електричних зарядів кульки на магнітну стрілку. У свою чергу, магнітне поле стрілки не діє на заряджену кульку. Отже, нерухомі електричні заряди не створюють магнітного поля і постійне магнітне поле не діє на нерухомі електричні заряди.
2. Взаємодія між постійним електричним
струмом і магнітною стрілкою
Якщо пропустити постійний струм I через провідник, то магнітна стрілка повернеться навколо своєї осі так, щоб стати перпендикулярно до провідника зі струмом (рис.1). Це явище відкрив Г. Ерстед. Він виявив, що напрямок повороту північного полюсу стрілки змінюється на протилежний, якщо поміняти напрямок струму в провіднику.

| Рис.42 |

| Рис.43 |
Щоб охарактеризувати магнітне поле, треба розглянути його дію на певний струм. Розглянемо замкнений плоский контур зі струмом, розміри якого малі порівняно з відстанню до струмів, що утворюють поле. За позитивний напрямок нормалі приймається напрямок поступального руху свердлика, головка якого обертається в напрямку струму, що тече в контурі (рис.2). Контур зі струмом характеризується магнітним моментом  , який дорівнює добутку сили струму І, що протікає у контурі, на площу поверхні контуру S :
, який дорівнює добутку сили струму І, що протікає у контурі, на площу поверхні контуру S :
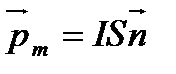 ,
,
де 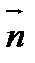 – одиничний вектор нормалі до поверхні рамки. Напрямок вектора
– одиничний вектор нормалі до поверхні рамки. Напрямок вектора  збігається з напрямком позитивної нормалі рамки.
збігається з напрямком позитивної нормалі рамки.
Контуром зі струмом можна скористатись і для кількісного опису магнітного поля. На контур у магнітному полі діє пара сил. Обертальний момент сил М залежить від властивостей контуру:
 .
.
Якщо контур зі струмом повернути на 90° від рівноважного положення, то на нього буде діяти максимальний обертальний момент Мmax.
Якщо в дане місце магнітного поля поміщати контури з різними магнітними моментами, то на них діятимуть різні обертальні моменти, але відношення Мmax/  , для всіх контурів однакове і є кількісною характеристикою магнітного поля:
, для всіх контурів однакове і є кількісною характеристикою магнітного поля:
 .
.
Магнітна індукція в даному місці магнітного поля визначається максимальним обертальним моментом, що діє на контур з одиничним магнітним моментом.
Одиниця магнітної індукції - тесла: 1 Тл — магнітна індукція такого магнітного поля, в якому на рамку з магнітним моменом  діє максимальний момент сили 1 Нм.
діє максимальний момент сили 1 Нм.
За напрямок індукції В магнітного поля приймається напрямок магнітного момента поля, який знаходиться в рівноважному положенні у цьому полі.
Для графічного зображення магнітних полів зручно користуватись лініями магнітної індукції. Лініями магнітної індукції називають такі лінії, дотичні до яких у кожній точці збігаються з напрямком вектора В в цих точках поля.
Напрямок ліній індукції магнітного поля струму визначається за правилом свердлика: якщо вкручувати свердлик за напрямком руху струму в провіднику, то напрямок руху його рукоятки покаже напрям ліній магнітної індукції.
Лінії магнітної індукції можна спостерігати за допомогою дрібних металевих ошурків, які в магнітному полі поводять себе як маленькі магнітні стрілки.
Узагальнюючи результати дослідження дії магнітного поля на різні провідники зі струмом, Ампер встановив, що сила  , з якою магнітне поле діє на елемент довжиним dl провідника зі струмом, що знаходиться в магнітному полі, прямо пропорційна до сили струму І в провіднику і до векторного добутку елемента довжини
, з якою магнітне поле діє на елемент довжиним dl провідника зі струмом, що знаходиться в магнітному полі, прямо пропорційна до сили струму І в провіднику і до векторного добутку елемента довжини  на магнітну індукцію В :
на магнітну індукцію В :
 .
.
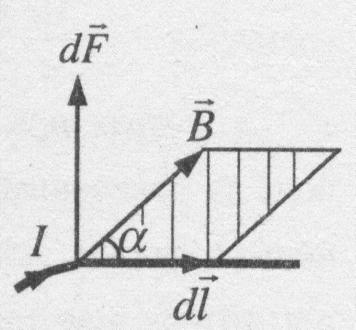
| Рис.44 |
 можна знайти за правилом векторного добутку і за правилом Е лівої руки: якщо долоню лівої руки поставити так, щоб у неї входили лінії магнітної індукції, а чотири витягнуті пальці спрямувати в напрямку електричного струму в провіднику, то відставлений на 90° великий палець покаже напрямок сили, що діє на провідник з боку поля. Це правило зручне, коли елемент провідника зі струмом перпендикулярний до напрямку магнітного поля.
можна знайти за правилом векторного добутку і за правилом Е лівої руки: якщо долоню лівої руки поставити так, щоб у неї входили лінії магнітної індукції, а чотири витягнуті пальці спрямувати в напрямку електричного струму в провіднику, то відставлений на 90° великий палець покаже напрямок сили, що діє на провідник з боку поля. Це правило зручне, коли елемент провідника зі струмом перпендикулярний до напрямку магнітного поля.
В загальному випадку для визначенням напрямку сили Ампера  слід скористатись правилом векторного добутку: вектор
слід скористатись правилом векторного добутку: вектор 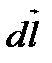 напрямлений перпендикулярно до площини, утвореної векторами
напрямлений перпендикулярно до площини, утвореної векторами  і В так, щоб з кінця вектора
і В так, щоб з кінця вектора 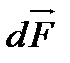 обертання від вектора
обертання від вектора 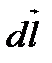 до вектора
до вектора 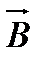 найкоротшим шляхом відбувалося проти годинникової стрілки (рис.3).
найкоротшим шляхом відбувалося проти годинникової стрілки (рис.3).
Модуль сили Ампера розраховується за формулою:
 ,
,
де  - кут між векторами
- кут між векторами  і
і  .
.
Припустимо, що елемент провідника dl із струмом I перпендикулярний до напрямку магнітного поля ( 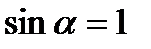 ), тоді закон Ампера можна записати у вигляді:
), тоді закон Ампера можна записати у вигляді:
 .
.
Отже, магнітна індукція є силовою характеристикою магнітного поля.
Лекція №16
31. Закон Біо-Савара-Лапласа
У 1920 р. французькі вчені Ж. Біо і Ф. Савар дослідили магнітні поля, створені в повітрі прямолінійним струмом, коловим струмом, котушкою із струмом тощо. їіа основі численних дослідів вони дійшли таких висновків:
а) у всіх випадках індукція В магнітного поля електричного струму пропорційна до сили струму I;
б) магнітна індукція залежить від форми і розмірів провідника із струмом;
в) магнітна індукція В у будь-якій точці поля залежить від розташування цієї точки відносно провідника зі струмом.
Біо і Савар намагалися знайти загальний закон, який дав би змогу обчислити магнітну індукцію в кожній точці поля, створеного електричним струмом, що протікає по провіднику будь-якої форми. Однак зробити це їм не вдалося. Розв’язав це завдання П. Лаплас.
Лаплас узагальнив результати експериментів Біо і Савара у вигляді такого диференціального закону, який називається закономБіо-Савара-Лапласа:
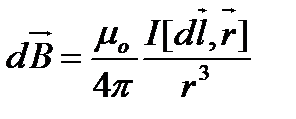 .
.

| Рис.45 |
 – вектор, що числово дорівнює довжині
– вектор, що числово дорівнює довжині  елемента провідника і збігається за напрямком з електричним струмом,
елемента провідника і збігається за напрямком з електричним струмом, 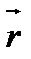 – радіус-вектор, проведений від елемента провідника
– радіус-вектор, проведений від елемента провідника  до точки поля А, що розглядається (рис.4),
до точки поля А, що розглядається (рис.4), 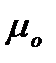 – магнітна стала.
– магнітна стала.
Отже, модуль індукції  магнітного поля малого елемента
магнітного поля малого елемента  провідника зі струмом прямо пропорційний до сили струму І, довжини елемента
провідника зі струмом прямо пропорційний до сили струму І, довжини елемента  провідника, обернено пропорційний до квадрата відстані r від елемента провідника до розглядуваної точки поля, а також залежить від кута
провідника, обернено пропорційний до квадрата відстані r від елемента провідника до розглядуваної точки поля, а також залежить від кута  між напрямками струму і радіус-вектора
між напрямками струму і радіус-вектора 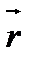 (рис.4):
(рис.4):
 .
.
Напрямок вектора  перпендикулярний до
перпендикулярний до  і
і  , тобто перпендикулярний до площини, в якій вони лежать, і збігається з дотичною до лінії магнітної індукції. Напрямок
, тобто перпендикулярний до площини, в якій вони лежать, і збігається з дотичною до лінії магнітної індукції. Напрямок  визначається з векторного добутку
визначається з векторного добутку 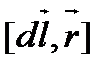 і може бути знайдений за правилом свердлика.
і може бути знайдений за правилом свердлика.
Дослід показує, що для магнітного поля справедливийпринцип суперпозиції: індукція магнітного поля, створеного декількома струмами або рухомими зарядами, дорівнює векторній сумі магнітних полів, що створені кожним струмом або рухомим зарядом окремо.
Відповідно до принципу суперпозиції магнітна індукція  у будь-якій точці магнітного поля провідника зі струмом І дорівнює векторній сумі індукцій
у будь-якій точці магнітного поля провідника зі струмом І дорівнює векторній сумі індукцій  елементарних магнітних полів, створених окремими ділянками
елементарних магнітних полів, створених окремими ділянками 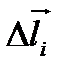 , цього провідника:
, цього провідника:
 .
.
Необмежене збільшуючи кількість ділянок п і переходячи до границі при п, що прямує до нескінченності, можна замінити суму інтегралом:
 .
.
Отже, магнітна індукція поля, яке створене у вакуумі струмом І , що тече по провіднику скінченної довжини і довільної форми, дорівнює
 .
.
Розрахунок характеристик магнітного поля за наведеними формулами в загальному випадку досить складний. Однак, якщо розподіл струму має певну симетрію, то застосування закону Біо-Савара-Лапласа разом з принципом суперпозиції дає змогу досить просто розрахувати магнітну індукцію конкретних полів.
Магнітне поле прямолінійного провідника з струмом. Магнітне поле колового струму
Розглянемо прямий провідник довільної форми, по якому проходить струм I, наприклад згори вниз (рис.164);
 Відповідно до закону Біо - Савара - Лапласа вектор магнітної індукції dB поля у вакуумі, створеного в точці А елементом dl провідника зі струмом, числово дорівнює
Відповідно до закону Біо - Савара - Лапласа вектор магнітної індукції dB поля у вакуумі, створеного в точці А елементом dl провідника зі струмом, числово дорівнює

де α- кут між векторами dl ' і r.
 У точці А, яка знаходиться на відстані R від осі провідника, всі вектори dВ, які характеризують магнітні поля, створені окремими ділянками цього провідника, напрямлені перпендикулярно до площини рисунка. Вектор В числово дорівнює алгебраїчній сумі модулів векторів dВ:
У точці А, яка знаходиться на відстані R від осі провідника, всі вектори dВ, які характеризують магнітні поля, створені окремими ділянками цього провідника, напрямлені перпендикулярно до площини рисунка. Вектор В числово дорівнює алгебраїчній сумі модулів векторів dВ:
Замінимо dl і r через одну незалежну змінну α
| Рис46 |

У результаті, індукція магнітного поля прямолінійного провідника МN у точці А дорівнює

Якщо провідник MN нескінченно довгий, то α1 = 0, а α2 = π. Отже, магнітна індукція нескінченно довгого провідника зі струмом дорівнює (cos0= 1, cos π =-1)

Знайдемо індукцію магнітного поля в центрі О, колового струму радіусом R, по
якому, протікає струм I (рис. 165):


| Рис.47 |
Усі вектори dВ магнітних полів, які створені в точці О різними ділянками, dl колового струму, напрямлені перпендикулярно до площини рисунка "від нас".
Тоді
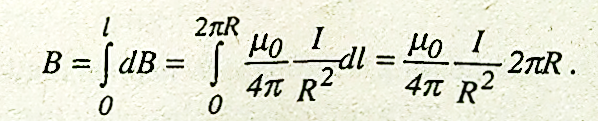
Отже, індукція магнітного поля колового струму дорівнює

32. Закон повного струму для магнітного
поля у вакуумі. Вихровий характер магнітного поля
Введемо циркуляцію вектора магнітної індукції. Циркуляцією вектора 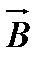 по замкненому контуру називається інтеграл
по замкненому контуру називається інтеграл
 ,
,
де  - вектор елемента довжини контуру, напрямлений вздовж обходу контуру,
- вектор елемента довжини контуру, напрямлений вздовж обходу контуру,  – проекція вектора
– проекція вектора  на дотичну до контуру,
на дотичну до контуру,  - кут між векторами
- кут між векторами  і
і  .
.
| Рис.48 |
 Розглянемо магнітне поле нескінченного прямолінійного провідника зі струмом І, що знаходиться у вакуумі (рис.5). Лінії магнітної індукції цього поля є кола, площини яких перпендикулярні до провідника, а центри лежать на осі провідника. Знайдемо циркуляцію вектора
Розглянемо магнітне поле нескінченного прямолінійного провідника зі струмом І, що знаходиться у вакуумі (рис.5). Лінії магнітної індукції цього поля є кола, площини яких перпендикулярні до провідника, а центри лежать на осі провідника. Знайдемо циркуляцію вектора  вздовж кола радіуса r. У всіх точках кола вектор
вздовж кола радіуса r. У всіх точках кола вектор  числово дорівнює
числово дорівнює
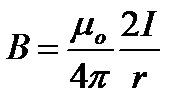
і напрямлений по доточній до кола, тому  .
.
Тоді
 .
.
Звідси можна зробити два висновки:
1) магнітне поле прямолінійного струму - вихрове поле, бо циркуляція вектора  вздовж ліній індукції не дорівнює 0;
вздовж ліній індукції не дорівнює 0;
2) циркуляція вектора  магнітної індукції поля прямолінійного струму однакова вздовж будь-якої лінії індукції і дорівнює
магнітної індукції поля прямолінійного струму однакова вздовж будь-якої лінії індукції і дорівнює 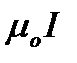 .
.
Цю формулу можна використати до замкненого контуру L довільної форми, який охоплює нескінченно довгий прямолінійний провідник зі струмом І.
Якщо контур  не охоплює провідник зі струмом, то
не охоплює провідник зі струмом, то
 .
.
У всіх випадках, які розглядались вище, кут  гострий, тобто з кінця вектора густини струму
гострий, тобто з кінця вектора густини струму  , напрямленого по осі провідника в бік струму, обхід по контуру
, напрямленого по осі провідника в бік струму, обхід по контуру 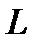 , відбувається проти стрілки годинника. При протилежному напрямку обходу контуру
, відбувається проти стрілки годинника. При протилежному напрямку обходу контуру 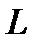 або при протилежному напрямку струму в провіднику отримуємо
або при протилежному напрямку струму в провіднику отримуємо
 .
.
Надалі використовуватимемо таке правило знаків струмів:
позитивним вважається струм, напрямок якого зв’язаний з напрямком обходу по контуру правилом свердлика; струм протилежного напрямку вважаєтьсянегативним.
На практиці магнітне поле, переважно, створюється кількома провідниками, по яких проходять струми І1, І2, І3 тощо. На основі принципу суперпозиції магнітна індукція  результуючого поля дорівнює
результуючого поля дорівнює
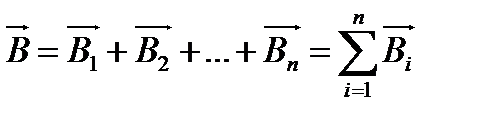 .
.
Тоді
 .
.
Кожен з інтегралів, що стоїть під знаком суми, дорівнює або 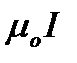 , якщо струм охоплюється контуром, або 0, якщо струм не охоплюється контуром.
, якщо струм охоплюється контуром, або 0, якщо струм не охоплюється контуром.
Отже,
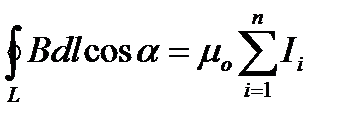 .
.
де п – кількість провідників зі струмами, що охоплюються контуром L довільної форми.
Рівняння  , є математичним виразом закону повного струму для струмів провідності:
, є математичним виразом закону повного струму для струмів провідності:
циркуляція вектора  по довільному замкненому контуру дорівнює добутку магнітної сталої
по довільному замкненому контуру дорівнює добутку магнітної сталої 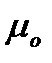 , на алгебраїчну суму струмів, що охоплюються цим контуром.
, на алгебраїчну суму струмів, що охоплюються цим контуром.
Отриманий вираз закону повного струму справедливий лише для магнітного поля у вакуумі, оскільки для поля у речовині слід враховувати молекулярні струми.
Лекція №17
33. Cила Лоренца
Виникнення макроскопічної сили Ампера, що діє на провідник із струмом у магнітному полі, можна пояснити так. При проходженні струму носії заряду в провіднику рухаються напрямлено. Тому магнітне поле відхиляє їх в один бік. При цьому вони стикаються з кристалічною граткою металу і передають їй певний імпульс, якого набули під дією магнітного поля. Макроскопічним результатом елементарних процесів зіткнення окремих носіїв заряду з кристалічною граткою провідника є виникнення сили Ампера.
Магнітне поле діє на вільні електрони в метал і і без електричного струму в провіднику. Оскільки електрони в цьому випадку рухаються тільки хаотично, то сумарний імпульс, який вони надають кристалічній гратці провідника, дорівнює нулю і провідник залишається нерухомим.
Для обчислення сили, що діє на рухомий заряд в магнітному полі, розглянемо елемент провідника dl зі струмом I у магнітному полі з індукцією  . На цей елемент діє сила Ампера
. На цей елемент діє сила Ампера 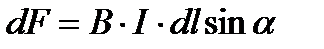 . Якщо елемент dl містить dN вільних носіїв заряду, то сила F, що припадає на один електрон, дорівнює:
. Якщо елемент dl містить dN вільних носіїв заряду, то сила F, що припадає на один електрон, дорівнює:
 ,
,
де FЛ – сила Лоренца.
Кількість носіїв заряду dN в елементі Провідника dl запишемо через їх концентрацію п та об’єм dV елемента:
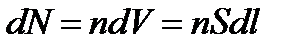 ,
,
S – площа поперечного перерізу провідника.
Тоді
 .
.
Оскільки за електронною теорією  , то
, то
 ,
,
або
 .
.
де  – кут між векторами
– кут між векторами  і
і  . В загальному випадку
. В загальному випадку
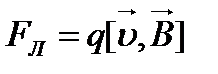 .
.
Напрямок сили Лоренца визначається за правилом векторного добутку або правилом лівої руки:
якщо долоню лівої руки розмістити так, щоб в неї входив вектор  , а чотири витягнуті пальці спрямовувати вздовж вектора швидкості
, а чотири витягнуті пальці спрямовувати вздовж вектора швидкості  руху позитивних зарядів, то відігнутий на 90° великий палець покаже напрямок сили, що діє на позитивний заряд.
руху позитивних зарядів, то відігнутий на 90° великий палець покаже напрямок сили, що діє на позитивний заряд.
На негативний заряд сила діє в протилежному напрямку (рис. 6).

| Рис. 6 |
| Рис.49 |
Якщо на рухомий електричний заряд, крім магнітного поля з індукцією  , діє і електричне поле з напруженістю
, діє і електричне поле з напруженістю 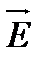 , то результуюча сила
, то результуюча сила  , яка прикладена до заряду:
, яка прикладена до заряду:
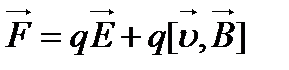 – формула Лоренца.
– формула Лоренца.
Якщо заряджена частинка рухається в магнітному полі зі швидкістю  вздовж ліній магнітної індукції або в протилежний бік до напрямку магнітної індукції, то
вздовж ліній магнітної індукції або в протилежний бік до напрямку магнітної індукції, то  або
або 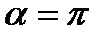 . У такому разі
. У такому разі  , магнітне поле на частинку не діє і вона рухається рівномірно і прямолінійно.
, магнітне поле на частинку не діє і вона рухається рівномірно і прямолінійно.
Якщо заряджена частинка рухається в магнітному полі з швидкістю  перпендикулярно до вектора
перпендикулярно до вектора  , то сила Лоренца постійна за модулем і нормальна до траєкторії частинки. Частинка рухатиметься по колу, бо сила Лоренца за другим законом Ньютона буде створювати доцентрове прискорення. Отже,
, то сила Лоренца постійна за модулем і нормальна до траєкторії частинки. Частинка рухатиметься по колу, бо сила Лоренца за другим законом Ньютона буде створювати доцентрове прискорення. Отже,
 .
.
Звідси
 ,
,
де r – радіус кола.
Використавши зв’язок  , знайдемо циклічну частоту
, знайдемо циклічну частоту  та період Т обертання частинки навколо ліній індукції в магнітному полі:
та період Т обертання частинки навколо ліній індукції в магнітному полі:
 ,
,  .
.
Період обертання частинки в однорідному магнітному полі не залежить від її швидкості (при  << c ). На цьому грунтується дія циклічних прискорювачів заряджених частинок.
<< c ). На цьому грунтується дія циклічних прискорювачів заряджених частинок.
Нехай навколо точкового заряду + q, який знаходиться у вакуумі, описано довільну замкнену поверхню S
| Рис.50 |

Лінії напруженості виходять з цієї поверхні. Виділимо довільну елементарну площадку ds, нормаль n до якої складає
кут α з вектором Е. Спроектуємо елемент ds поверхні S на поверхню радіуса r з центром в місці знаходження заряду q.
ТодіdSп =dSсоsα. Елементарний потік

а dώ -тілесний кут, під яким елементарну площадку ds видно з точкового зарядуq.
Провівши інтегрування по куту, отримаємо
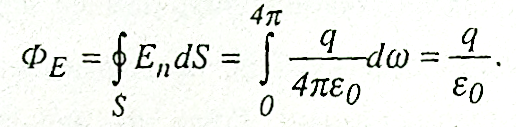
Якщо всередині замкненої поверхні буде негативний заряд, то кут між нормаллю і вектором Е буде тупий (лінії напруженості входять всередину замкненої поверхні). Отже, соsа < 0. Тоді dФЕ < 0. Це означає, що потік через замкнену поверхню

 Нехай всередині замкненої поверхні S буде N позитивних і негативних зарядів (рис. 109). За принципом суперпозиції напруженість Е поля, що створюється
Нехай всередині замкненої поверхні S буде N позитивних і негативних зарядів (рис. 109). За принципом суперпозиції напруженість Е поля, що створюється
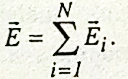
всіма зарядами, дорівнює сумі напруженостей Е, що створюється кожним зарядом зокрема і .
Тому проекція вектора Е на напрямок нормалі до площадки dS дорівнює алгебраїчній сумі проекцій всіх векторів Еi на цей напрямок:

Потік вектора напруженості результуючого поля через довільну замкнену поверхню S, що охоплює заряди q1,q2,..qn дорівнює

Отже, потік вектора напруженості у вакуумі через довільну замкнену поверхню, яка охоплює електричні заряди, дорівнює алгебраїчній сумі цих зарядів, поділеній на електричну сталу
Це твердження називається теоремою Остроградського-Гаусса.
Наприклад, для системи зарядів, які наведені на рис.109, потік напруженості
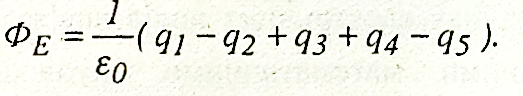
Якщо замкнена поверхня S не охоплює заряд q (риє. 110), то дотична до
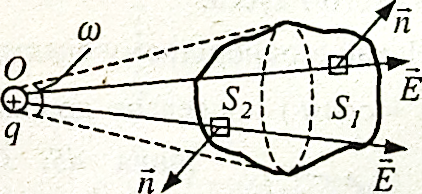
поверхні S конічна поверхня з вершиною у точці О поділяє поверхню S , на дві частини:
S1 i S2.
Потік напруженості через поверхню 5 дорівнює сумі потоків: >
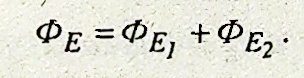
Потоки ФЕ1 і ФЕ2 дорівнюють один одному за абсолютною величиною, тому що поверхні S1 і S2 видно з точки О під тим самим тілесним кутом ώ. Оскільки для всіх елементів поверхні S1 кути між векторами Е і зовнішніми нормалями n гострі, а для поверхні S2 ці кути тупі, то

Тому сумарний потік через поверхню 8
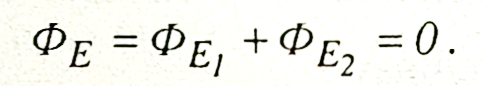
Нехай заряд q знаходиться всередині замкненої поверхні S і лінії напруженості перетинають цю поверхню кілька разів (риc.111).
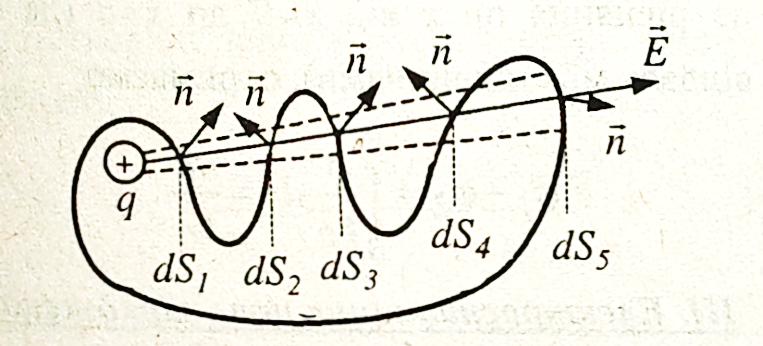
Елементарний потік напруженості через площадки dS1….. dS2 дорівнює

Отже, непарне число перетинів при обчисленні потоку,напруженості зводиться до одного перетину.
34. Контур зі струмом у магнітному колі
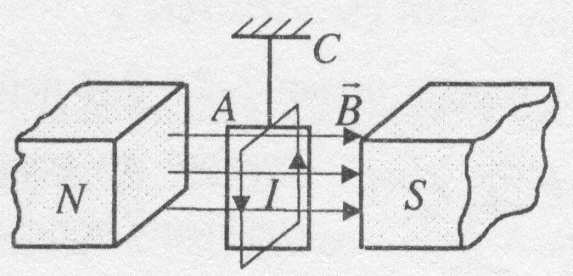 Розглянемо поведінку в магнітному полі замкнених провідників зі струмом. Помістимо в однорідне магнітне поле електромагніту провідник, який зігнутий у вигляді прямокутної рамки А, що підвішена на пружній нитці С (рис.8) .
Розглянемо поведінку в магнітному полі замкнених провідників зі струмом. Помістимо в однорідне магнітне поле електромагніту провідник, який зігнутий у вигляді прямокутної рамки А, що підвішена на пружній нитці С (рис.8) .
| Рис.52 |
| Рис.51 |
| Рис. 9 |
 магнітної індукції поля. Рамка із струмом завжди встановлюється у зовнішньому однорідному магнітному полі в тому положенні, при якому власний магнітний момент
магнітної індукції поля. Рамка із струмом завжди встановлюється у зовнішньому однорідному магнітному полі в тому положенні, при якому власний магнітний момент 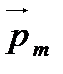 рамки збігається з напрямком
рамки збігається з напрямком  . З кінця цього вектора ми бачимо, що струм у рамці йде проти стрілки годинника.
. З кінця цього вектора ми бачимо, що струм у рамці йде проти стрілки годинника.
| Рис. 10 |
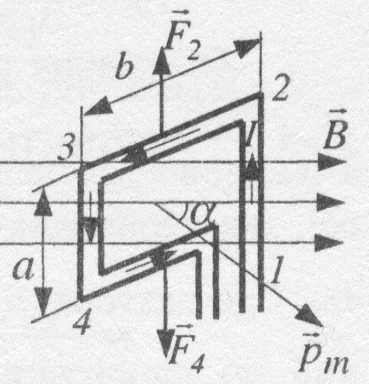
 утворює кут
утворює кут  з вектором
з вектором  власного магнітного моменту рамки (рис.9). Сторони рамки 2-3 і 4-1 лежать у площинах, паралельних до індукції зовнішнього магнітного поля
власного магнітного моменту рамки (рис.9). Сторони рамки 2-3 і 4-1 лежать у площинах, паралельних до індукції зовнішнього магнітного поля  .
.
Сили  і
і  напрямлені вздовж вертикальної осі рамки у протилежні боки. Вони деформують рамку у вертикальному напрямку.
напрямлені вздовж вертикальної осі рамки у протилежні боки. Вони деформують рамку у вертикальному напрямку.
| Рис.53 |
 магнітної індукції поля (рис.10). Сили
магнітної індукції поля (рис.10). Сили 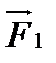 і
і  , які прикладені до прямолінійних провідників 1-2 і 3-4, числово дорівнюють:
, які прикладені до прямолінійних провідників 1-2 і 3-4, числово дорівнюють:
 .
.
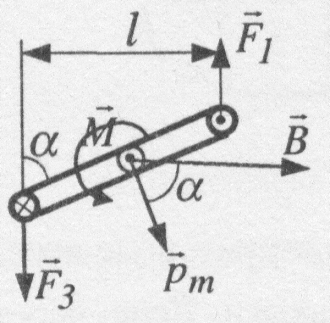
Результуючий обертальний момент М, який діє на рамку, дорівнює моменту нари сил  і
і  , тобто
, тобто 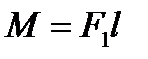 , де
, де  . Тоді
. Тоді
 ,
,
де S = ab – площа рамки, IS = pm – числове значення вектора магнітного моменту рамки зі струмом. Тоді

Обертання рамки під дією пари сил 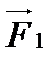 і
і  відбувається навколо вертикальної осі, яка перпендикулярна як до вектора
відбувається навколо вертикальної осі, яка перпендикулярна як до вектора  , так і до вектора
, так і до вектора  . Вектор
. Вектор  напрямлений до спостерігача перпендикулярно до площини рисунка.
напрямлений до спостерігача перпендикулярно до площини рисунка.
Вектор обертального моменту 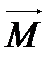 , який діє на рамку зі струмом у магнітному полі, дорівнює векторному добутку магнітного моменту
, який діє на рамку зі струмом у магнітному полі, дорівнює векторному добутку магнітного моменту  рамки на магнітну індукцію
рамки на магнітну індукцію 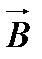 зовнішнього поля:
зовнішнього поля:
 .
.
Обертальний момент  дорівнює нулю і контур перебуває в рівновазі, якщо магнітний момент контуру паралельний або антипаралельний до напрямку зовнішнього поля (
дорівнює нулю і контур перебуває в рівновазі, якщо магнітний момент контуру паралельний або антипаралельний до напрямку зовнішнього поля (  ). Стійким є тільки таке положення контуру, коли вектори
). Стійким є тільки таке положення контуру, коли вектори  і
і  паралельні один до одного.
паралельні один до одного.
35. Магнітний потік.
Теорема Остроградського-Ґаусса
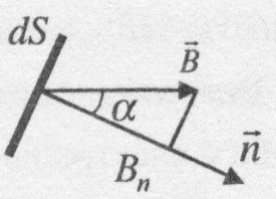
Потоком вектора магнітної індукції (магнітним потоком) через площину dS називається скалярна фізична величина, яка дорівнює
 .
.
| Рис. 11 |
 – проекція вектора
– проекція вектора  на напрямок нормалі до плоoини dS (
на напрямок нормалі до плоoини dS (  – кут між векторами
– кут між векторами  і
і  ) (рис. 11),
) (рис. 11),  – вектор, модуль якого дорівнює dS, а напрямок збігається з нормаллю й до площини.
– вектор, модуль якого дорівнює dS, а напрямок збігається з нормаллю й до площини.
| Рис.54 |
 може бути як позитивним, так і негативним залежно від знака cos
може бути як позитивним, так і негативним залежно від знака cos  (визначається вибором позитивного напрямку нормалі
(визначається вибором позитивного напрямку нормалі 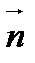 ).
).
Потік вектора магнітної індукції ФВ через довільну поверхню S дорівнює
 .
.
Для однорідного поля і плоскої поповерхні, розміщеної перпендикулярно до вектора  ,
,  і
і 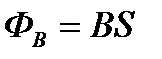 .
.
Розрахуємо потік вектора  через соленоїд. Всередині соленоїда індукція однорідного поля у вакуумі дорівнює
через соленоїд. Всередині соленоїда індукція однорідного поля у вакуумі дорівнює
 .
.
Магнітний потік через один виток меноїда площею S:
 .
.
Повний магнітний потік через соленоїд, який називається потокозчепленням 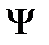 , дорівнює:
, дорівнює:
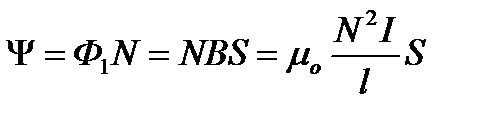 .
.
В електродинаміці доводиться теорема Остроградського-Ґаусса для магнітного поля: магнітний потік крізь довільну замкнену поверхню дорівнює нулю:
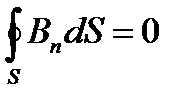 .
.
Ця теорема є наслідком того, що в природі нема магнітних “зарядів” і лінії індукції будь-якого магнітногополя є замкненими кривими.
36. Робота переміщення провідника і контуру
зі струмом у магнітному полі

| Рис. 12 |
| Рис.55 |
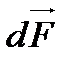 , яка діє на нього. Робота dA дорівнює:
, яка діє на нього. Робота dA дорівнює:
 .
.
За законом Ампера
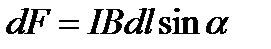 .
.
Тоді
 .
.
Сила 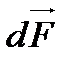 і переміщення
і переміщення  напрямлені перпендикулярно до елемента провідника
напрямлені перпендикулярно до елемента провідника 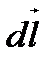 .
.
Добуток  – площа поверхні, яка описана елементом провідника dl при його переміщенні на dx.
– площа поверхні, яка описана елементом провідника dl при його переміщенні на dx.
З рис. 12 видно, що  – проекція вектора
– проекція вектора 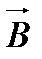 на напрямок нормалі
на напрямок нормалі 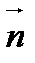 до площини dS.
до площини dS.
Добуток  - магнітний потік крізь поверхню dS. Тоді
- магнітний потік крізь поверхню dS. Тоді
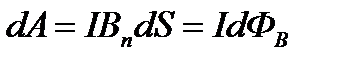 .
.
Вважаючи силу струму сталою і, інтегруючи цей вираз, отримаємо
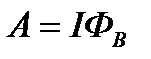 .
.
Робота, яку виконує сила Ампера при перевищенні в магнітному полі провідника, струм в якому постійний, дорівнює добутку сили струму на величину магнітного потоку крізь поверхню, яку описує провідник під час свого руху.

| Рис. 56 |
Нехай внаслідок нескінченно малого переміщення контур С зайняв положення С¢ (рис.13).
Контур С уявно розіб’ємо на два з’єднані своїми кінцями провідники АМD і DNA. Повна робота dА, виконана силами Ампера при розглядуваному переміщенні контуру, дорівнює алгебраїчній сумі робіт переміщення провідників АМD (dА1) і DNA (dА2), тобто dА = dА1 + dА2.
Припустимо, що вектор 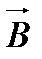 магнітної індукції напрямлений перпендикулярно до площини рисунка і в початковому положенні контуру дорівнює В1 а в кінцевому-В2, причому В2>В1.
магнітної індукції напрямлений перпендикулярно до площини рисунка і в початковому положенні контуру дорівнює В1 а в кінцевому-В2, причому В2>В1.
Сила Ампера 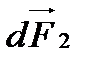 , що діє на довільний елемент dl2, утворює гострий кут з напрямком його переміщення
, що діє на довільний елемент dl2, утворює гострий кут з напрямком його переміщення  і виконує позитивну роботу.
і виконує позитивну роботу.
Сила 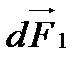 , що діє на елемент dl1 Провідника АМО, утворює з напрямком його переміщення
, що діє на елемент dl1 Провідника АМО, утворює з напрямком його переміщення  тупий кут і виконує негативну роботу, тому роботи dA1 і dА2 переміщення провідників АМD і DNA мають різні знаки. Щоб отримати абсолютні значення роботи dA1 і dА2, треба продиференціювати вираз
тупий кут і виконує негативну роботу, тому роботи dA1 і dА2 переміщення провідників АМD і DNA мають різні знаки. Щоб отримати абсолютні значення роботи dA1 і dА2, треба продиференціювати вираз  . Тому
. Тому
 ,
,
де  - магнітний потік крізь поверхню AMDD¢M¢A¢;
- магнітний потік крізь поверхню AMDD¢M¢A¢;  – крізь поверхню ANDD¢N¢A¢;
– крізь поверхню ANDD¢N¢A¢;  – зміна магнітного потоку, що пронизує поверхню, обмежену контуром, при переміщенні контуру з положення С в положення С¢.
– зміна магнітного потоку, що пронизує поверхню, обмежену контуром, при переміщенні контуру з положення С в положення С¢.
Остаточний вираз для елементарної роботи dА буде
 .
.
Інтегруючи цей вираз, знайдемо роботу А, яку виконує сила Ампера при будь-якому переміщенні контуру в магнітному полі
 .
.
Робота, яку виконуює сила Ампера при переміщенні в магнітному полі замкненого контуру, по якому проходить постійний струм, дорівнює добутку сили струму на зміну магнітного потоку крізь поверхню, обмежену контуром.
Матеріал для самостійної роботи
Читайте також:
- Аксоплазма
- Грошові агрегативідрізняються насамперед своєю ліквідністю.
- Для транснаціональних корпорацій прямі іноземні інвестиції є найкращим способом управління і контролю за своєю діяльністю за кордоном.
- Екзистенціалізм належить до тих напрямів, які відповідають на це питання: світ не розумний, він абсурдний за своєю природою.
- Електричний опір провідників. Надпровідність
- Електричний стум в газах. Плазма
- Ендоплазматична сітка
- За своєю спрямованістю ДЦП поділяються на економічні, наукові, науково-технічні, соціальні, національно-культурні, екологічні, оборонні, правоохоронні та ін.
- МЕМБРАНИ МІКРОБНИХ КЛІТИН. Цитоплазматична мембрана.
- Особливості ран, нанесених гострими предметами при заподіянні їх своєю і чужою рукою (при самогубствах і убивствах).
- Плазма крові
| <== попередня сторінка | | | наступна сторінка ==> |
| Плазма – особливий стан речовини з майже повною іонізацією частинок речовини, у якій густина додатніх та від’ємних частинок майже однакова. | | |
|
Не знайшли потрібну інформацію? Скористайтесь пошуком google: |
© studopedia.com.ua При використанні або копіюванні матеріалів пряме посилання на сайт обов'язкове. |