• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Алгоритм

1. Через пряму загального положення проводять допоміжну січну площину (горизонтально- або фронтально-проекціювальну)

(рис. 27, а, б, в).

Рисунок 27 – Варіанти введення допоміжної січної площини γ

2. Знаходять пряму перетину а заданої площини σ з введеною січною площиною γ (рис. 28, а, б).

Рисунок 28 – Побудова лінії перетину а з допоміжною січною площиною γ

3.

Рисунок 29 – Побудова точки перетину Кз площиною

4. Визначають видимість прямої, використовуючи конкуруючі точки 1, 3 та 2, 4 (рис. 30, а, б, в).

Рисунок 30 – Варіанти введення конкуруючих точок

4.1. Щоб визначити видимість прямої на П₂, виділимо частину проекції прямої l₂ дугою. Т.К₂ – проекція точки перетину. На цьому ж проміжку точки 1 та 3 конкурують (1 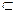а, 3 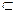l). Видимою на П₂ буде точка 1, точка 3 – невидима (рис. 30, б), оскільки У₁ > У₃. А це означає, що частина прямої l, яка виділена дугою, невидима (точка 3 невидима та належить прямій l). Частина проекції l₂, яка обмежена проекціями К₂ та 3₂, закривається площиною, тобто невидима.

4.2. Для визначення видимості прямої l на П₁ виділимо частину проекції l₁ дугою. На цьому проміжку позначимо конкуруючі точки 4 та 5 (4 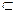l, 5 в), т.4 – видима, т.5 – невидима (рис. 30, б). Враховуючи те, що т.4 належить прямій l, виділену частину проекції l₂ наводимо суцільною основною лінією. Решта частини прямої, яка знаходиться в межах контуру площини, – невидима.

Підсумовуючи пояснення щодо загального випадку перетину прямої з площиною, запишемо алгоритм розв’язання цієї задачі в символьній формі (див. зазначені пункти розв’язання задачі):

1. l ≡ γ, γ П_2.
2. γ ∩ σ = d.
3. 

4. Видимість l.

5.3 Приклади для закріплення

Приклад 1. За наочним зображенням побудуйте проекції точки перетину прямої з площиною.

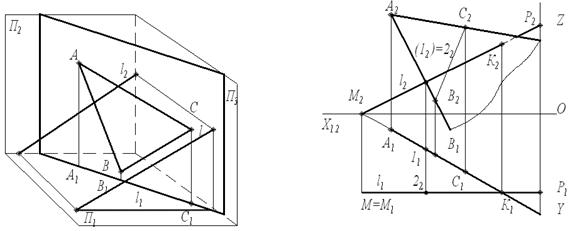
1. Площина ∆ АВС займає горизонтально-проекціювальне положення. Значить, горизонтальна проекція точки К₁ визначається безпосередньо на перетині сліду проекції ∆ А₁В₁С₁ з проекцією l₁.

2. Пряма l займає фронтальне положення і має точки перетину М з площиною П₁ та Р з площиною П₃. Як видно з побудов, проекція точки перетину К₂ виходить за межі трикутника, тому для визначення видимості l на П₂ проекції А₂В₂ та А₂С₂ слід продовжити. Пряма до точки К знаходиться перед сторонами АВ та АС (див. проекції конкуруючих точок 1 та 2). Це означає, що відрізок МК прямої l на П₂ видимий.

Приклад 2. Визначте проекції точок перетину прямої l загального положення з площиною загального положення, яка задана трикутником (рис. 31, а, б).

Для пояснення введемо символьні позначення.

Дано: l ∩ ∑ (∆ АВС) = К (К₁, К₂).

Побудувати: К (К₁, К₂).

Читайте також:

1. Rete-алгоритм
2. АЛГОРИТМ
3. Алгоритм
4. Алгоритм
5. АЛГОРИТМ
6. Алгоритм 1.
7. Алгоритм 2
8. Алгоритм RLE
9. Алгоритм адресного вибору оптимального безрецептурного вітаміновмісного лікарського препарату, лікарської форми і шляху введення
10. Алгоритм безпосередньої заміни
11. Алгоритм Берлекемпа-Мессі

Переглядів: 951