• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция

Розв’язання.

Розвинемо функції 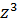та в ряд Лорана за степенями (z – 1):

Тоді

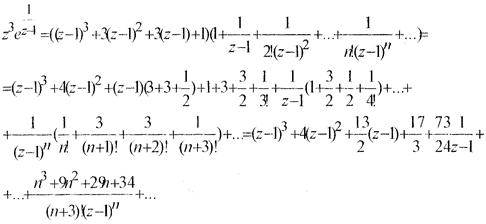
Отже правильна частина ряду Лорана функції дорівнює .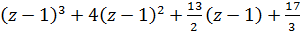

Головна частина цього ряду –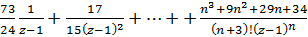

§17. Ізольовані, особливіточки

Нехай функція f(z) регулярна в кільці 0 < |z – z₀| < ρ, але не регулярна в точці z₀(z₀≠ ∞). Тоді точка z₀ називається ізольованою особливою точкою однозначного характеру для функції f(z).

Нескінченно віддалена точка називається ізольованою особливою точкою однозначного характеру для функції f(z), якщо функція f(z) регулярна в області ρ < |z| < ∞.

В залежності від поведінки функції f(z) в околі точки z₀ розрізняють наступні три типи особливих точок.

Ізольована особлива точка z₀ однозначного характеру f(z)називається:

а) усувною особливою точкою, якщо 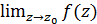існує і скінченний;

б) полюсом, якщо ;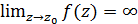

в) істотно особливою точкою, якщо 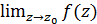не існує.

Зв’язок між розкладом функції f(z) в ряд Лорана в околі точки z = z₀ та характером особливості цієї точки встановлюється наступними теоремами:

Теорема 1. Для того, щоб ізольована особлива точка z₀ була усувною особливою точкою функції f(z), необхідно і достатньо, июб головна частина ряду Лорана в околі точки z₀ була тотожньо рівною нулю.

Теорема 2. Для того, щоб ізольована особлива точка z = z₀ була полюсом для функції f(z) і, необхідно і достатньо, щоб головна частина ряду Лорана для функції f(z) в околі точки z₀ містила лише скінченне число членів.

Теорема 3. Для того, щоб ізольована особлива точка z = z₀ була істотно особливою точкою для функції f(z), необхідно і достатньо, щоб головна частина ряду Лорана в околі точки z₀ містила нескінченну кількість членів.

Завдання 75. довести, що точка z₀ є усувною особливою точкою функції f(z):

1) .

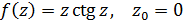Розв’язання:

Знайдемо границю даної функції при z → 0

Границя існує і скінченна, тому точка z₀ = 0 є усувною особливою точкою функції .

Завдання 76. Знайти полюси функції f(z), і встановити порядок цих полюсів:

1) ;

Розв’язання:Знайдемо нулі знаменника і визначимо їх порядок.

z² – z – 2 = 0при z₁ = –1, z₂ = 2. Порядок цих нулів другий. Так як при z₁ = –1та z₂ = 2чисельник не дорівнює і, то це є полюси заданої функції другого порядку.

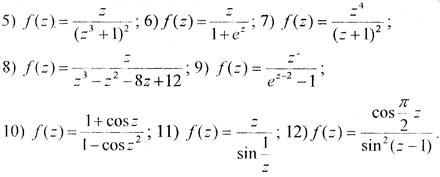
Завдання 77. Довести, що точка z₀ є істотно особливою точкою функції f(z).

1) .

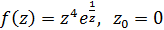Розв’язання: Розвинемо дану функцію в ряд Лорана в околі точки z₀ = 0:

Головна частина цього ряду 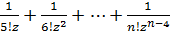містить скінчену кількість членів, отже точка z₀ = 0 є істотно особливою точкою функції .

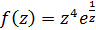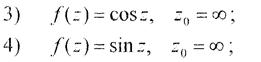
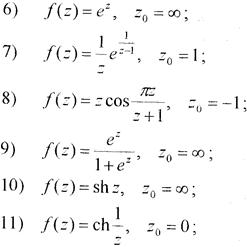
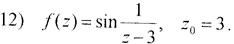
Завдання 78. Знайти ізольовані особливі точки аналітичної функції і з’ясувати їх характер:

1)

Розв’язання:Ізольованими особливими точками даної функції є точки z₁ = 2i, z₂ = –2i. Так як це нулі знаменники першого порядку і чисельник в цих точках не дорівнює нулю, то точки z₁ = 2i і z₂ = –2i є простими полюсами функції .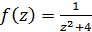

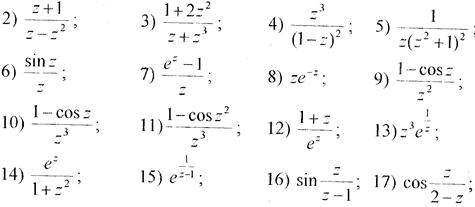
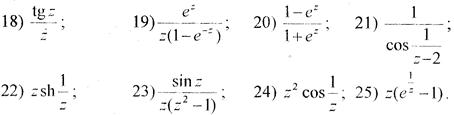
§18. Лишки.

Коефіцієнт С_–1 в розкладі в ряд Лорана

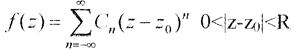
однозначної аналітичної функції f(z) в околі скінченної ізольованої особливої точки z₀ називається лишком цієї функції відносно точки z₀і позначається . Лишок через інтеграл подається формулою

де С_ρ – коло |z – z₀| = ρ, 0 < ρ < R.

Лишок в усувній точці дорівнює нулю.

Якщо точка z = z₀ є простим полюсом функції f(z), то лишок в цій точці обчислюється за формулою:

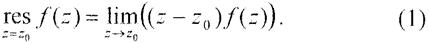
Якщо точка z = z₀ полюс порядку m функції f(z), то лишок в ній обчислюється за формулою:

Лишком функції f(z) в точці z = ∞ (позначається ) називається число –С_-1, де С_-1 – коефіцієнт при ряду Лорана для функції f(z) в околі нескінченно віддаленої точки.

де – коло |z| = ρ, орієнтоване за годинниковою стрілкою.

Якщо функція f(z) аналітична в нескінченно віддаленій точці, то

де під символом f(∞) розуміють .

При обчисленні лишків доцільно використовувати наступне твердження.

Нехай функція f(z) регулярна у всій розширенній комплексній площині, за виключенням скінченого числа особливих точок. Тоді сума всіх лишків функції f(z), включаючи лишок в точці z = ∞, дорівнює нулю:

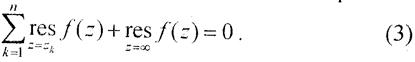
Завдання 79.Знайти лишки функції f(z) в її скінченних ізольованих особливих точках:

1) .

Розв’язання:Особливими точками даної функції є точки z = 0 та z = 7. Точка z = 0 – простий полюс. За формулою (1) маємо

Точка z = 7 полюс другого порядку, тому за формулою (2) маємо

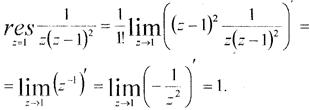
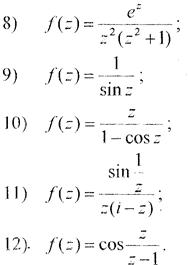
Завдання 80. Обчислити лишки функції f(z) в усіх особливих точках і в точці z = ∞.

1) .

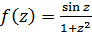Розв’язання:Особливими точками функції є z₁ = –i, z₂ = i, z₃ = ∞. За формулою (1)

Лишок в нескінченно віддаленій точці знайдемо із співвідношення (3)

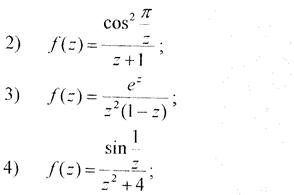
19. Обчисленняінтегралівпозамкненомуконтуру.

Читайте також:

1. Актуальні проблеми регіональної політики та їх розв’язання.
2. Вказівки до розв’язання.
3. Міжнаціональні відносини і причини виникнення міжнаціональних конфліктів, шляхи їх розв’язання. Міжконфесійні стосунки та їх вплив на життя в полікультурному суспільстві
4. Поняття біосфери та ноосфери. Поняття екології. Основні завдання соціальної екології. Сучасні екологічні проблеми, причини їх виникнення та розв’язання.
5. Розв’язання.
6. Розв’язання.
7. Розв’язання.
8. Розв’язання.
9. Розв’язання.
10. Розв’язання.
11. Розв’язання.
12. Розв’язання.

Переглядів: 3284