• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция

Нормальний закон розподілу.

Нормальнимназивається розподіл ймовірності неперервної випадкової величини, яке описується щільністю ймовірності

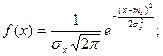(1.3.5.1)

Нормальний закон розподілу також називається законом Гауса.

Параметри 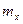та 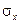, які входять в щільність розподіли є відповідно математичним очікуванням і середнім квадратичним відхиленням випадкової величини Х.

Функцію розподілу F(x).

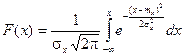(1.3.5.2)

При 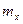= 0 і 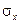=1розподіл називається нормованим нормальним розподілом

(1.3.5.3)

Інтегральна функція

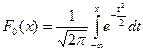(1.3.5.4)

Обидві функції протабульовані (додаток 2, додаток 3)

Графік щільності нормального розподілу називається нормальною кривоюабо кривою Гауса.

Нормальна крива володіє наступними властивостями:

1) Функція визначена на всій числовій осі.

2) При всіх х функція розподілу приймає тільки позитивні значення.

3) Вісь ОХ є горизонтальною асимптотою графіка щільності ймовірності.

4) Графік функції f(x) перетинає вісь ОY в точці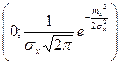

5) Функція має максимум в точці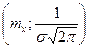

6) Функція є симетричною відносно прямою х = ,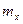

7) Графік функції має точки перегибу в точках ,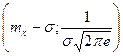

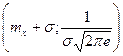
Побудуємо графік функції щільності розподілу.

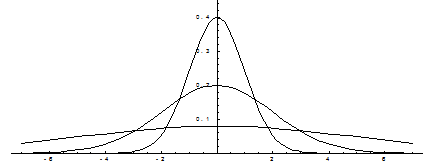
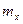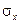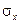Побудовані графіки при =0 і трьох можливих значеннях середнього квадратичного відхилення = 1, = 2 і 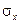= 7. Як видно, при збільшенні значення середнього квадратичного відхилення графік стає пологішим, а максимальне значення зменшується.

Знайдемо ймовірність попадання випадкової величини, розподіленої по нормальному закону, в заданий інтервал.

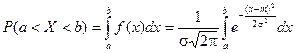(1.3.5.5)

Позначимо

Тоді (1.3.5.6)

де

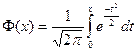(1.3.5.7)

функція Лапласаабо інтеграл ймовірності (таблиця - додаток 3)

При розгляді нормального закону розподілу виділяється важливий часний випадок, відомий як правило трьох сигм.

Запишемо ймовірність того, що відхилення нормально розподіленої випадкової величини від математичного очікування менше заданої величини ∆:

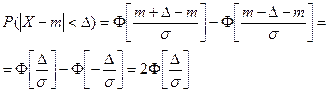(1.3.5.8)

Якщо прийняти ∆ = 3σ, то отримуємо з використанням таблиць значень функції Лапласа:

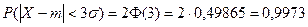(1.3.5.9)

Тобто ймовірність того, що випадкова величина відхилиться від свого математичного очікування на величину, більшу чим потрійне середнє квадратичне відхилення, практично рівна нулю.

Це правило називається правилом трьох сигм.

Не практиці вважається, що якщо для якої-небудь випадкової величини виконується правило трьох сигм, то ця випадкова величина має нормальний розподіл.

Читайте також:

1. II. Закон кийка та ікла
2. II. Основні закономірності ходу і розгалуження судин великого і малого кіл кровообігу
3. III закон Ньютона
4. IV. Закони ідеальних газів.
5. IV. Закономірності структурно-функціональної організації спинного мозку
6. IV. СПИСОК РЕКОМЕНДОВАНОЇ ЛІТЕРАТУРИ І ЗАКОНОДАВСТВА.
7. А) Грошовий обіг. Закони.
8. Або зі зберігання інформації та забезпечення доступу до неї, за умови, що ця особа не могла знати про незаконність розповсюдження інформації.
9. Авілум – “син чоловіка” – повноправна людина, охороні його життя, здоров’я, захисту його майнових інтересів присвячена значна частина законника.
10. Агностицизм, сторонники которого отрицают возможность достоверного познания сущности материального мира, закономерностей развития природы и общества.
11. Аграрне право та законодавство США, Німеччини, Франції, Великої Британії, Ізраїлю, Польщі, Росії
12. Аграрні закони України

Переглядів: 1963