• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Надійний інтервал для оцінки математичного очікування нормального розподілу.

Нехай кількісна ознака X генеральної сукупності розподілена нормально, причому середнє квадратичне відхилення σ цього розподілу відомо.

Потрібно оцінити відоме математичне очікування а по вибірковій середній 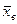. Поставимо своїм завданням знайти надійні інтервали, що покривають параметр а з надійністю γ.

Розглядатимемо вибіркову середню 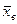як випадкову величину ( 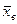змінюється від вибірки до вибірки)

і вибіркові значення ознаки х₁, х₂ ..., х_п- як однаково розподілені незалежні випадкові величини X₁, X₂ ...,Х_п (ці числа також змінюються від вибірки до вибірки). Іншими словами, математичне очікування кожною з цих величин рівно а і середнє квадратичне відхилення -σ.

Приймемо без доведення, що якщо випадкова величина X розподілена нормально, то вибіркова середня , знайдена в незалежних спостереженнях, також розподілена нормально. Параметри розподілу такі

М ( ) = а, σ ( ) = .

Необхідно, щоб виконувалося співвідношення

Р(| -а| <δ)= γ

Користуючись формулою (1.3.5.8)

замінивши X на , т на а і σ на σ ( ) = , отримаємо

Р (| - а |< δ) = 2Ф( ) = 2Ф (t) (2.2.3.1)

де t =

Знайшовши з останньої рівності δ = , можемо записати

Р (| - а |< ) = 2Ф (t)

Прийнявши до уваги, що ймовірність Р задана і рівна γ, остаточно маємо (щоб отримати робочу формулу, вибіркову середню знов позначимо через )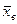

Р ( 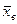- |< а|< 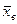+ ) = 2Ф (t)=γ (2.2.3.2)

Зміст отриманого співвідношення такий: з надійністю γ можна стверджувати, що надійний інтервал ( 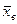- ; 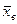+ ) покриває невідомий параметр а; точність оцінки

δ=

Число t визначається з рівності 2Ф(t)= γ або Ф(t) = γ/2; по таблиці функції Лапласа (див. додаток 3) знаходиться аргумент t, якому відповідає значення функції Лапласа, рівне γ/2

ЗауваженняНадійну ймовірність не слід пов'язувати з оцінюваним параметром; вона зв'язана лише з межами надійного інтервалу, які, як вже було вказано, змінюються від вибірки до вибірки.

Читайте також:

1. А) Мета і об'єкти грошової оцінки
2. Адекватним фізичним критерієм оцінки її впливу на організм люди1
3. Аналіз відхилень – основний інструмент оцінки діяльності центрів відповідальності
4. Аналіз відхилень — основний інструмент оцінки діяльності центрів відповідальності
5. Аналіз впливу зміни температури довкілля і термо-залежного параметру на величину відхилення часових інтервалів
6. Аналіз загальної рівноваги розширює можливості оцінки ефективності функціонування ринкової економіки.
7. Аналіз методичних підходів до оцінки конкурентоспроможності фірми
8. Ануїтет та його значення для оцінки інвестицій
9. АПВ з очікуванням синхронузму
10. Атестація як особливий метод оцінки персоналу
11. Атестація як система оцінки співробітників.
12. Аудиторський ризик і методи його оцінки

Переглядів: 1187