
РЕЗОЛЮЦІЯ: Громадського обговорення навчальної програми статевого виховання
ЧОМУ ФОНД ОЛЕНИ ПІНЧУК І МОЗ УКРАЇНИ ПРОПАГУЮТЬ "СЕКСУАЛЬНІ УРОКИ"
ЕКЗИСТЕНЦІЙНО-ПСИХОЛОГІЧНІ ОСНОВИ ПОРУШЕННЯ СТАТЕВОЇ ІДЕНТИЧНОСТІ ПІДЛІТКІВ
Батьківський, громадянський рух в Україні закликає МОН зупинити тотальну сексуалізацію дітей і підлітків
Відкрите звернення Міністру освіти й науки України - Гриневич Лілії Михайлівні
Представництво українського жіноцтва в ООН: низький рівень культури спілкування в соціальних мережах
Гендерна антидискримінаційна експертиза може зробити нас моральними рабами
ЛІВИЙ МАРКСИЗМ У НОВИХ ПІДРУЧНИКАХ ДЛЯ ШКОЛЯРІВ
ВІДКРИТА ЗАЯВА на підтримку позиції Ганни Турчинової та права кожної людини на свободу думки, світогляду та вираження поглядів
- Гідрологія і Гідрометрія
- Господарське право
- Економіка будівництва
- Економіка природокористування
- Економічна теорія
- Земельне право
- Історія України
- Кримінально виконавче право
- Медична радіологія
- Методи аналізу
- Міжнародне приватне право
- Міжнародний маркетинг
- Основи екології
- Предмет Політологія
- Соціальне страхування
- Технічні засоби організації дорожнього руху
- Товарознавство продовольчих товарів
Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция
Аналіз впливу зміни температури довкілля і термо-залежного параметру на величину відхилення часових інтервалів
Методичні вказівки до виконання лабораторних робіт з дисципліни
Адаптивні системи керування і контролю
для студентів 4 року навчання напряму підготовки
6.050202 – Автоматизація та комп’ютерно-інтегровані технології
Київ – 2014
Зміст
Лабораторна робота №1……………………………………... 3
Визначення оптимуму однопараметричних систем.
Частина 1. Інтервальні оцінки статистичних показників синхросигналів екстремальної комп’ютерно-інтегрованої системи керування технологічними процесами обробки даних в цифрових телекомунікаційних мережах………………………………………... 3
Частина 2. Скалярна оптимізація екстремальної комп’ютерно-інтегрованої системи керування технологічними процесами обробки даних в цифрових телекомунікаційних мережах……………………………………………………………….. 17
Додаток 1 до лабораторної роботи №1.
Статистичний аналіз умов виготовлення та експлуатації електронних пристроїв екстремальної комп’ютерно-інтегрованої системи керування технологічними процесами обробки даних в цифрових телекомунікаційних мережах………………………………… 22
Лабораторна робота №1
Визначення оптимуму однопараметричних систем.
Частина 1. Інтервальні оцінки статистичних
Показників синхросигналів екстремальної комп’ютерно-інтегрованої системи керування технологічними процесами обробки даних в цифрових телекомунікаційних мережах
Мета роботи: отримання практичних навичок дослідження статистичних показників синхросигналів екстремальної комп’ютерно-інтегрованої системи керування технологічними процесами обробки даних в цифрових телекомунікаційних мережах
Теоретичні відомості
Необхідність статистичного дослідження показників синхросигналів екстремальної комп’ютерно-інтегрованої системи керування технологічними процесами обробки даних в цифрових телекомунікаційних мережах
Необхідність статистичного дослідження однієї з найважливіших характеристик сигналів синхронізації (синхросигналів) - часового інтервалу викликана самою природою виникнення цієї погрішності: статистичним характером умов експлуатації територіально розподілених цифрових телекомунікаційних мереж, в яких комп’ютерно-інтегрована система забезпечує керування технологічними процесами обробки даних й умов транспортування (переміщення) синхроінформації, а також неминучим розкидом параметрів апаратури.
Статистичний підхід до розгляду механізму утворення сумарного відхилення часових інтервалів доцільно робити з послідовною його деталізацією аж до обліку впливу на сумарну нестабільність і особливо на її температурну складову параметрів кожної деталі, що входить у пристрій. Це дає, з одного боку, розрахунковий апарат для визначення обґрунтованих допусків на параметри вузлів і деталей пристроїв, з іншого боку, дозволяє підійти до обґрунтованого визначення умов оптимальної температурної стійкості часових інтервалів синхросигналів екстремальної комп’ютерно-інтегрованої системи керування технологічними процесами обробки даних в цифрових телекомунікаційних мережах, та визначення заходів, на основі застосування сучасних досягнень електротехніки, щодо підвищення стабільності по деяким складовим впливів.
Аналітичне формулювання задачі статистичного дослідження синхросигналів комп’ютерно-інтегрованої системи керування технологічними процесами обробки даних в цифрових телекомунікаційних мережах
Експериментальне дослідження екстремальної комп’ютерно-інтегрованої системи підтвердило те, що періодичні відліки часу синхросигналів є випадковою величиною.
Базуючись на такому факті визначимо, з використанням статистичних методів розрахунку, фактичну робочу величину відхилення часових інтервалів синхросигналів в умовах реальної експлуатації обладнання екстремальної комп’ютерно-інтегрованої системи і його серійного виробництва.
Окрім визначення величини відхилення часових інтервалів необхідно визначити область довіри. В силу того, що ця область може змінюватися від вибірки до вибірки можна говорити лише про ймовірність того, що така область покриває дійсне значення параметру. Відповідно цьому, якщо задатися досить малим числом 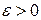 , то можна визначити правило згідно якому з вірогідністю
, то можна визначити правило згідно якому з вірогідністю 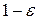 дійсне значення параметру буде потрапляти в визначену область довіри в параметричному просторі.
дійсне значення параметру буде потрапляти в визначену область довіри в параметричному просторі.
Теоретичною передумовою для ймовірнісного дослідження відхилення часових інтервалів синхросигналів екстремальної комп’ютерно-інтегрованої системи можна рахувати граничну теорему Ляпунова, яка свідчить, що ці випадкові величини підкоряються закону Гауса, якщо їх можна розглядати як суму нескінченно великого числа взаємно незалежних випадкових величин {ℓк, к≥1} з функціями розподілу Gк(х)=Р{ℓк,< х}. Важливо відзначити, що ці випадкові величини повинні задовольняти умовам Ляпунова відносно питомої ваги окремих доданків в загальній сумі і умовам Бернштейна відносно тісноті зв'язків окремих доданків між собою [1, 2].
При виконанні цих умов, що практично завжди з необхідною точністю буває в реальних умовах, щільність вірогідності сумарного відхилення часових інтервалів синхросигналів екстремальної комп’ютерно-інтегрованої системи керування технологічними процесами обробки даних може бути представлена у вигляді:
 (1)
(1)
де 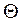 - сумарне відхилення часових інтервалів;
- сумарне відхилення часових інтервалів; 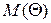 - математичне очікування сумарного відхилення часових інтервалів;
- математичне очікування сумарного відхилення часових інтервалів;  - дисперсія сумарного відхилення часових інтервалів, а саме розподілення є нормальним розподілом з невідомими параметрами. Задачею є оцінка параметрів цього розподілу. Оцінювання параметрів полягає в визначенні статистик, що є функціями вибіркових значень.
- дисперсія сумарного відхилення часових інтервалів, а саме розподілення є нормальним розподілом з невідомими параметрами. Задачею є оцінка параметрів цього розподілу. Оцінювання параметрів полягає в визначенні статистик, що є функціями вибіркових значень.
З огляду на те, що сумарна величина відхилення часових інтервалів визначається окремими практично незалежними складовими, то необхідно окремо для кожної складової ℓк, к=1,…,m визначити закон розподілу і його статистики. Потім, відповідно до правил теорії вірогідності, обчислити необхідні статистики вже для сумарної величини відхилення часових інтервалів, а саме  і
і 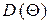 , по формулах:
, по формулах:
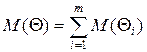 (2)
(2)
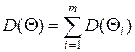 (3)
(3)
де 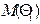 і
і  - відповідно середні значення і дисперсії окремих складових величини відхилення часових інтервалів.
- відповідно середні значення і дисперсії окремих складових величини відхилення часових інтервалів.
Для визначення інтервалу довіри 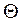 макс усередині якого можуть знаходиться практично всі значення відхилення часових інтервалів задамося коефіцієнтом довіри 1-e=0,997. Тоді для нормального закону розподілу практично гранична зміна величини відхилення часових інтервалів
макс усередині якого можуть знаходиться практично всі значення відхилення часових інтервалів задамося коефіцієнтом довіри 1-e=0,997. Тоді для нормального закону розподілу практично гранична зміна величини відхилення часових інтервалів 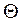 макс буде визначаться з рівняння [1, 2]:
макс буде визначаться з рівняння [1, 2]:
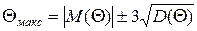 (4)
(4)
На підставі запропонованої вище методики з врахуванням експериментально отриманих результатів перейдемо до визначення закону розподілу і його оцінок для окремих складових. Виділимо три складові сумарної величини відхилення часових інтервалів, а саме, зміна напруги живлення, зміна частоти синхронізуючого сигналу, зміна температури довкілля.
Аналіз впливу зміни температури довкілля і термо-залежного параметру на величину відхилення часових інтервалів
Територіально розподілені пристрої формування синхросигналів екстремальної комп’ютерно-інтегрованої системи в більшості випадків, експлуатуватимуться в різних кліматичних умовах. Тому виникає необхідність у дослідженні показників синхросигналів, які залежать від температури довкілля. Такою залежною величиною є відхилення часових інтервалів від температури довкілля. Поясненням цієї залежності є те, що практично всіх параметри елементів екстремальної комп’ютерно-інтегрованої системи керування технологічними процесами обробки даних залежать в тій чи іншій мірі від температури.
Відхилення часових інтервалів при зміні температури довкілля представимо у вигляді
 (5)
(5)
де 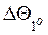 - величина відхилення часових інтервалів при зміні температури довкілля на 1оС;
- величина відхилення часових інтервалів при зміні температури довкілля на 1оС; 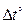 - відхилення температури від значення, при якому виконувалась настройка пристрою. Величина
- відхилення температури від значення, при якому виконувалась настройка пристрою. Величина 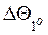 є випадковою величиною, оскільки вона визначається параметрами, які в процесі виробництва мають деякий розкид, елементарних складових екстремальної комп’ютерно-інтегрованої системи керування технологічними процесами обробки даних в цифрових телекомунікаційних мережах. Відхилення температури
є випадковою величиною, оскільки вона визначається параметрами, які в процесі виробництва мають деякий розкид, елементарних складових екстремальної комп’ютерно-інтегрованої системи керування технологічними процесами обробки даних в цифрових телекомунікаційних мережах. Відхилення температури 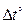 від вихідного значення також є випадковим величиною, яка залежить від умов експлуатації цифрових управляючих систем. На підставі цього і враховуючи статистичну незалежність
від вихідного значення також є випадковим величиною, яка залежить від умов експлуатації цифрових управляючих систем. На підставі цього і враховуючи статистичну незалежність 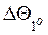 і
і 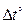 з врахуванням теореми про множину двох незалежних випадкових величин визначимо математичне очікування і дисперсію
з врахуванням теореми про множину двох незалежних випадкових величин визначимо математичне очікування і дисперсію 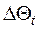
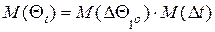 (6)
(6)
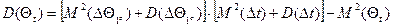 (7)
(7)
Визначимо математичне очікування зміни температури.
Вважаючи рівномірним закон розподілу температури в межах, які задаються при розробці апаратури можна записати (рис.1):
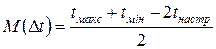 (8)
(8)
 (9)
(9)
де 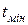 і
і  - відповідно максимальне і мінімальне значення температури при якій передбачається робота апаратури екстремальної комп’ютерно-інтегрованої системи, задане технічними умовами;
- відповідно максимальне і мінімальне значення температури при якій передбачається робота апаратури екстремальної комп’ютерно-інтегрованої системи, задане технічними умовами;  - температура при якій виконувалась настройка.
- температура при якій виконувалась настройка.
 |
Визначимо статистики термо-залежного параметра 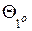 - відхилення часових інтервалів при зміні температури довкілля на 1оС. Величина
- відхилення часових інтервалів при зміні температури довкілля на 1оС. Величина 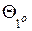 є випадковою величиною, що пояснюється, по-перше, умовами серійного виробництва апаратури і, по-друге, залежністю результуючого відхилення часових інтервалів при зміні температури на 1оС від суми елементарних складових зсуви, які визначаються чималою кількістю окремих деталей екстремальної комп’ютерно-інтегрованої системи керування технологічними процесами обробки даних. Таким чином, можна стверджувати, що розподіл ймовірності окремих значень відхилення часових інтервалів підпорядкований закону Гауса (рис.1), а математичне очікування відхилення часових інтервалів при зміні температури на 1оС визначається з формули:
є випадковою величиною, що пояснюється, по-перше, умовами серійного виробництва апаратури і, по-друге, залежністю результуючого відхилення часових інтервалів при зміні температури на 1оС від суми елементарних складових зсуви, які визначаються чималою кількістю окремих деталей екстремальної комп’ютерно-інтегрованої системи керування технологічними процесами обробки даних. Таким чином, можна стверджувати, що розподіл ймовірності окремих значень відхилення часових інтервалів підпорядкований закону Гауса (рис.1), а математичне очікування відхилення часових інтервалів при зміні температури на 1оС визначається з формули:
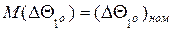 (10)
(10)
і відповідно дисперсія з наступної формули:
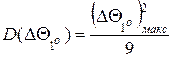 (11)
(11)
де 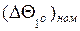 і
і  - відповідно номінальне і максимальне значення розкиду відхилення часових інтервалів при зміні температури на 1оС.
- відповідно номінальне і максимальне значення розкиду відхилення часових інтервалів при зміні температури на 1оС.
Підставляючи (24) і (10) в рівняння (6), а (11) і (9) в рівняння (7) відповідно отримуємо вирази для середнього значення і дисперсії відхилення часових інтервалів при зміні температури довкілля
 (12)
(12)
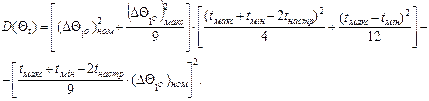 (13)
(13)
На основі отриманих аналітичних залежностей виконаємо розрахунок відхилення часових інтервалів від температури в умовах реальної експлуатації обладнання і з врахуванням його серійного виробництва.
Читайте також:
- ABC-XYZ аналіз
- I визначення впливу окремих факторів
- I етап. Аналіз впливу типів ринку на цінову політику.
- I. Аналіз контрольної роботи.
- II. Багатофакторний дискримінантний аналіз.
- III етап. Аналіз факторів, що визначають цінову політику підприємства.
- IV. Критерій питомої потенціальної енергії деформації формозміни
- IІI розділ. Аналіз стану маркетингового середовища підприємства
- SWOT-аналіз у туризмі
- SWOT-аналіз.
- Tема 4. Фації та формації в історико-геологічному аналізі
- V. Нюховий аналізатор
| <== попередня сторінка | | | наступна сторінка ==> |
| | | Залежність точності формування періодичних відліків часу від зміни напруги живлення в умовах реальної експлуатації обладнання екстремальної комп’ютерно-інтегрованої системи |
|
Не знайшли потрібну інформацію? Скористайтесь пошуком google: |
© studopedia.com.ua При використанні або копіюванні матеріалів пряме посилання на сайт обов'язкове. |