• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Сутність кількісного регресійного аналізу

Кількісний регресійний аналіз є продовженням парного регресійного аналізу у випадках, коли залежна змінна у пов’язана з двома або більше незалежними змінними х. Тобто відбувається розширення парної регресійної моделі, де важливе значення відіграють спільний вплив незалежних змінних на залежну змінну. Тому в кількісному регресійному аналізі необхідно враховувати й чітко визначити цей вплив, а також важливе значення має вирішення проблеми специфікації. Остання проблема лежить в площині вибору тих факторів, які впливають на результуючий показник, економічно інтерпретуються і об’єктивно відображають господарські процеси, що відбуваються на підприємстві. Результатом кількісного регресійного аналізу є побудова кількісної (багатофакторної) регресійної моделі.

В загальному вигляді, кількісна регресійна модель має вигляд:

y = а₀ + а₁x₁ + а₂х₂ +…+ а_іх_і + е, або

у = b + k₁x₁ + k₂x₂ +…+k_ix_i + e (10.1)

де y – результуюча залежна змінна;

х₁, х₂, х_і - незалежна змінна;

а₀, а₁, а₂, а_і, b, k₁, k₂, k_i – параметри рівняння (коефіцієнти регресії);

е – випадковий член.

У кількісному регресійному аналізі визначається коефіцієнт регресії, який необхідний для забезпечення найкращої відповідності спостереженням і отримання оптимальних оцінок невідомих значень параметрів моделей.

У кількісному регресійному аналізі визначається коефіцієнт регресії, який необхідний для забезпечення найкращої відповідності спостереженням і отримання оптимальних оцінок невідомих значень параметрів моделей.

Для розрахунку коефіцієнтів регресії , , 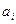використовуються методом найменших квадратів. Так для пошуку коефіцієнтів регресії (параметрів) двохфакторної моделі складають систему нормальних рівнянь:

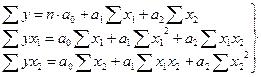. (10.2)

Кількісний регресійний аналіз дозволяє розмежовувати вплив незалежних змінних, допускаючи при цьому можливість їх корельованості. Коефіцієнт регресії для кожної змінної х дає оцінку її впливу на величину у у випадку незмінності впливу на неї всіх інших змінних х.

Це може бути встановлено двома способами. Один з них складається в виявленні того, що якщо модель правильно специфікована і виконуються умови Гауса-Маркова, то оцінки будуть незміщеними. Інший спосіб складається в оцінюванні регресійної залежності у від однієї з незалежних змінних, усунути перед цим можливість використання останньої в якості заміщувальної для іншої будь-якої незалежної змінної і показавши далі, що оцінка її коефіцієнта регресії співпадає з оцінкою коефіцієнта кількісної регресії. В рамках висвітлених способів необхідно розглянути умови Гауса-Маркова [20].

Якість коефіцієнтів регресії залежить від якості випадкового члена. Для того, щоб регресійний аналіз давав найкращі результати, випадковий член повинен задовольняти 4 умовам, відомим як умови Гауса-Маркова.

1-а умова Гауса-Маркова – складається в тому, що математичне очікування випадкового члена будь-якого спостереження повинно дорівнювати нулю.

2-а умова Гауса-Маркова – складається в тому, що дисперсія випадкового члену повинна бути постійною для всіх спостережень.

3-а умова Гауса-Маркова припускає відсутність систематичного зв’язку між значення випадкового члену в будь-яких спостереженнях. Випадкові члени повинні бути абсолютно незалежними один від одного.

4-а умова Гауса-Маркова – складається в тому, що випадковий член повинен бути розподілений незалежно від пояснювальних змінних. Тобто пояснювальні змінні не є стохастичними. Значення будь-якої незалежної змінної в кожному спостереженні повинно бути визначено зовнішніми причинами, які не визначені в рівнянні регресії.

Коефіцієнти регресії є більш точними:

1) чим більша кількість спостережень у виборці;

2) чим більша дисперсія вибірки пояснювальних змінних;

3) чим менша теоретична дисперсія випадкового члену;

4) чим менше зв’язані між собою пояснювальні змінні.

Стандартна помилка коефіцієнта кількісної регресії визначається аналогічно, як і в парному регресійному аналізі. Тобто формула для стандартної помилки може бути визначена на основі заміни дисперсії на незміщену оцінку і витягування квадратного кореню.

Результатом кількісного регресійного аналізу є побудова багатофакторної економетричної моделі, яка відображає причинно-наслідкові зв’язки між економічними факторами і створює кількісне підґрунтя для розробки економічних механізмів і прийняття ефективних управлінських рішень.

Читайте також:

1. T. Сутність, етіологія та патогенез порушень опорно-рухової системи
2. Автоматизовані системи управлінні охороною праці, обліку, аналізу та дослідження травматизму
3. Автомати­зовані інформаційні систе­ми для техніч­ного аналізу товар­них, фондових та валют­них ринків.
4. Алгебра та початки аналізу
5. Алгоритм однофакторного дисперсійного аналізу за Фішером. Приклад
6. Аналіз зображувальних засобів. Застосування цілісного аналізу
7. Аналіз руху грошових коштів у контексті нової фінансової звітності Важливим завданням аналізу фінансового стану підприємства є оцінка руху грошових коштів підприємства.
8. Аналізу соціальної взаємодії присвячено чимало наукових теорій.
9. АНАЛІЗУ ТА ПІДВЕДЕННЯ ПІДСУМКІВ СТАНУ ВІЙСЬКОВОЇ ДИСЦИПЛІНИ.
10. Аналізування предмету дослідження БКР
11. Аналізуюче схрещування
12. Аналізуючи малюнок, зробіть висновок, яке твердження правильне.

Переглядів: 551