
РЕЗОЛЮЦІЯ: Громадського обговорення навчальної програми статевого виховання
ЧОМУ ФОНД ОЛЕНИ ПІНЧУК І МОЗ УКРАЇНИ ПРОПАГУЮТЬ "СЕКСУАЛЬНІ УРОКИ"
ЕКЗИСТЕНЦІЙНО-ПСИХОЛОГІЧНІ ОСНОВИ ПОРУШЕННЯ СТАТЕВОЇ ІДЕНТИЧНОСТІ ПІДЛІТКІВ
Батьківський, громадянський рух в Україні закликає МОН зупинити тотальну сексуалізацію дітей і підлітків
Відкрите звернення Міністру освіти й науки України - Гриневич Лілії Михайлівні
Представництво українського жіноцтва в ООН: низький рівень культури спілкування в соціальних мережах
Гендерна антидискримінаційна експертиза може зробити нас моральними рабами
ЛІВИЙ МАРКСИЗМ У НОВИХ ПІДРУЧНИКАХ ДЛЯ ШКОЛЯРІВ
ВІДКРИТА ЗАЯВА на підтримку позиції Ганни Турчинової та права кожної людини на свободу думки, світогляду та вираження поглядів
- Гідрологія і Гідрометрія
- Господарське право
- Економіка будівництва
- Економіка природокористування
- Економічна теорія
- Земельне право
- Історія України
- Кримінально виконавче право
- Медична радіологія
- Методи аналізу
- Міжнародне приватне право
- Міжнародний маркетинг
- Основи екології
- Предмет Політологія
- Соціальне страхування
- Технічні засоби організації дорожнього руху
- Товарознавство продовольчих товарів
Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция
Напрями побудови лінійної моделі множинної регресії
Для побудови лінійної моделі множинної регресії використовується статистична інформація про діяльність підприємства і здійснюються такі етапи: математико-статистичний аналіз, побудова багатофакторної регресійної моделі, перевірка побудованої моделі на адекватність, аналіз (інтерпретація) отриманих результатів.
На етапі математико-статистичного аналізу проводиться перевірка основних припущень класичного регресійного аналізу, крім того, здійснюється найважливіша процедура багатофакторного аналізу – перевірка факторів на мультиколінеарність. Слід відзначити, що термін “мультиколінеарність” означає, що в багатофакторній регресійній моделі дві або більше незалежних змінних (факторів) пов’язані між собою лінійною залежністю або, іншими словами, мають високий ступінь кореляції (rxixj ® 1, i ¹ j).
Для здійснення математико-статистичного аналізу будується матриця коефіцієнтів парної кореляції, який показує ступінь зв’язку між факторами економетричної моделі. Потім аналізуються коефіцієнти парної кореляції між факторами. Результатом етапу математико-статистичного аналізу є знаходження множини основних незалежних між собою факторів, що є базою для побудови регресійної моделі.
На другому етапі для побудови багатофакторної моделі вибираються фактори, що будуть відображати причинно-наслідковий зв’язок. В цьому аспекті широке використання отримали «покроковий» метод і метод “виключень”.
Найбільш доцільно відшукувати рівняння множинної регресії шляхом послідовного підключення до парного рівняння решти аргументів в порядку їх значущості («покроковий метод»). У цьому випадку виявляється можливість на кожному етапі аналізувати:
- обумовленість вирішуваної системи за чисельним значенням її визначника (детермінатора);
- зміна β- коефіцієнтів, чисельне значення яких має бути менше 1, а знак не суперечити логіці;
- зростання коефіцієнта множинної кореляції R і убування залишкової дисперсії  .
.
Методика послідовного підключення аргументів складається з наступних операцій.
1.Обирається аргумент х1, якому відповідає найбільший за абсолютним значенням "зовнішній коефіцієнт" кореляції
| r y1| = max | r yi|, j = 1,2….q. (10.3)
За аргументом х1 записується рівняння
ty1 = ty1 tx1. (10.4)
2.Приєднюється аргумент хio, для якого
| r xj X1 | = min | r xj x1 |, j = 2,3,… q. (10.5)
Складається система нормальних рівнянь
r yх1 = β1 + r хjo β2; (10.6)
r y xjo = β1 r хjo x1 + β2 (10.7)
і обчислюються значення β1 и β2. Визначаються
R2y, x1 хjo = β1 ryx1 + β2 r y xjo; (10.8)
σу, х1 xjo =  (10.9)
(10.9)
Порівнюється R2y, x1 хjo, σу, х1 xjo відповідно з r 2yx1, σу х1.
Переконуються в справедливості нерівності
R2y, x1 хjo ≥ r 2yx1 ; σу, xjo ≤ σу х1. (10.10)
У противному разі замінюється чинник аргумент іншим хj1, а аргумент Xj0 переноситься на останнє місце.
3.Далі приєднується наступний аргумент Xj1 і розв'язується система з трьома невідомими:
r y х1 = β1 + β2 rх1 xjo + β3 rх1 xj1; (10.11)
r y xjo = β1 rх1 xjo + β2 + β3 r xjo xj1; (10.12)
r y xj1 = β1 rх1 xjo + β2 r xjo xj1 + β3. (10.13)
Обчислюються значення β1, β2 и β3. Визначаються
R2y, x1 хjo xj1 = β1 r y х1 + β2 r y xjo + β3 r y xj1; (10.14)
σу, xjo xj1 = σу 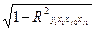 . (10.15)
. (10.15)
і порівнюються з R2y, x1 хjo і σу, x1 хjo. Переконуються в справедливості нерівності
R2y, x1 хjo xj1 ≥ R2y, x1 хjo; (10.16)
σу, x1 хjo xj1 ≤ σу, x1 хjo. (10.17)
У противному разі поступають аналогічно П.2.
Дослідження ведуть до тих пір, поки не будуть апробовані чинники-аргументи і збережені тільки ті з них, для яких βj–коефіцієнти суттєві й лінійно незалежні. У результаті виходить множинне рівняння в стандартизованому масштабі.
Від рівняння множинної регресії в стандартизованому масштабі
t 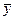 xi = β1 t1 + β2 t2 + ….+ βp tn (10.18)
xi = β1 t1 + β2 t2 + ….+ βp tn (10.18)
до рівняння множинної регресії в натуральному масштабі
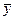 х1, х2…Хр = а1х1 + а2х2 + ….+ архр +b. (10.19)
х1, х2…Хр = а1х1 + а2х2 + ….+ архр +b. (10.19)
Перехід здійснюється подвійно.
1.Шляхом використання формул
 (10.20)
(10.20)
При цьому маємо
 (10.21)
(10.21)
Підставивши відомі значення 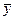 , σxi, σу, βi і
, σxi, σу, βi і 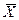 I, отримаємо рівняння множинної регресії в натуральному масштабі, в якому чисельне значення вільного члена додатково визначати не потрібно.
I, отримаємо рівняння множинної регресії в натуральному масштабі, в якому чисельне значення вільного члена додатково визначати не потрібно.
2.Невідомі коефіцієнти аi в рівнянні множинної регресії в натуральному масштабі визначають з виразу
 . (10.22)
. (10.22)
Чисельне значення вільного члена
b = 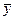 -(а1
-(а1 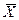 1+ а2
1+ а2 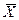 2 + …+ ар
2 + …+ ар 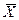 р). (10.23)
р). (10.23)
Метод “виключень” складається в тому, що вибирається набор факторів, які ймовірно можуть впливати на результативний показник. Потім, почерзі виключаються ті фактори, у який найменший коефіцієнт кореляції (згідно матриці статистики), а значення часткових F-критеріїв неперевищуюють нормативні значення. Таким чином, залишаться лише ті змінні, які відповідають розглянутим вище умовам.
Слід вказати, що на цьому етапі розраховується коефіцієнт множинної кореляції, який показує загальний вплив незалежних факторів на результуючий показник економетричної моделі. Він знаходиться у проміжку між 0 і 1. Чим більше вплив факторів, тим коефіцієнт множинної кореляції наближається до 1. Він не може перевищувати значення останньої.
Розрахунок коефіцієнта множинної кореляції ( 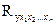 ) розраховується за формулою Боярського [18]:
) розраховується за формулою Боярського [18]:
 , (10.24)
, (10.24)
де  – порядок повної матриці коефіцієнтів кореляції;
– порядок повної матриці коефіцієнтів кореляції;
 – визначник повної матриці коефіцієнтів кореляції із заміною нижнього правого елемента нулем;
– визначник повної матриці коефіцієнтів кореляції із заміною нижнього правого елемента нулем;
 - визначник матриці, в якій враховані коефіцієнти парної кореляції незалежних факторів.
- визначник матриці, в якій враховані коефіцієнти парної кореляції незалежних факторів.
Якщо розкрити визначники для двохфакторної економетричної моделі, то коефіцієнт множинної кореляції може бути визначений:
 , (10.25)
, (10.25)
де  ,
,  - коефіцієнти парної кореляції між залежною змінною у і незалежними факторами х1, х2;
- коефіцієнти парної кореляції між залежною змінною у і незалежними факторами х1, х2;
 - коефіцієнт парної кореляції між незалежними змінним х1, х2.
- коефіцієнт парної кореляції між незалежними змінним х1, х2.
З метою контролю правильності розрахунків цей коефіцієнт визначають також за формулою [18]:
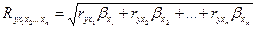 . (10.26)
. (10.26)
де  -
-  -коефіцієнти для незалежних факторів економетричної моделі. Цей коефіцієнт може бути розрахований наступним чином [18]:
-коефіцієнти для незалежних факторів економетричної моделі. Цей коефіцієнт може бути розрахований наступним чином [18]:
 , (10.27)
, (10.27)
де  – визначник (детермінант) матриці взаємної кореляції (мультиколінеарності) із заміною в ній і-го стовпця стовпцем коефіцієнтів кореляції
– визначник (детермінант) матриці взаємної кореляції (мультиколінеарності) із заміною в ній і-го стовпця стовпцем коефіцієнтів кореляції  . Наприклад,
. Наприклад,  -коефіцієнти для одного з факторів двохфакторної моделі разраховуються наступним чином:
-коефіцієнти для одного з факторів двохфакторної моделі разраховуються наступним чином:
 . (10.28)
. (10.28)
Знайдені в результаті рішення кореляційної матриці β-коефіцієнти показують на яку частину середньоквадратичного відхилення σу змінюється середнє значення функції, якщо відповідний аргумент зменшується або збільшується, а інші аргументи залишаються незмінними.
Для з'ясування математико-статистичного змісту множинної кореляції всю досліджувану групу змінних слід розглядати як один чинник-аргумент. При цьому розраховується коефіцієнт надійності
М =  . (10.29)
. (10.29)
Стандартну помилку (середню квадратичну похибку) коефіцієнта множинної кореляції визначають за формулою
σR = (1-R)/  , (10.30)
, (10.30)
де n-обсяг вибірки.
Сукупний вплив врахованих змінних на функцію визначається коефіцієнтом загальної детермінації R2, а окремих чинників-аргументів за чисельними значеннями приватної детермінації riβi:
R2 = r1β1 + r2β2+…..+ rpβp. (10.31)
Стандартну (систематичну) похибку  2 обчислюють за формулою
2 обчислюють за формулою
 2 = 1-(1- R2)
2 = 1-(1- R2)  , (10.32)
, (10.32)
де Р - число параметрів рівняння регресії. З рівняння множинної регресії можна отримати рівняння чистої (приватної) регресії  по кожному з аргументу хi. Для цього фіксується значення всіх аргументів, окрім хi, на середньому рівні.
по кожному з аргументу хi. Для цього фіксується значення всіх аргументів, окрім хi, на середньому рівні.
Отримане рівняння описує, як в середньому змінюється із зміною хi, якщо всі інші аргументи постійні й закріплені саме на своїх середніх рівнях.
Приклад. Розрахуйте коефіцієнт множинної кореляції та визначте  -коефіцієнти, на основі даних представлених в табл. 10.1.
-коефіцієнти, на основі даних представлених в табл. 10.1.
Таблиця 10.1. Матриця статистики економічних показників
| Показники | Коефіцієнти парної кореляції | ||
| Р (у) (рентабельність продукції) | ФЗоз (х1) (фондоозброєність основних засобів) | Ч (х2) (середньоспискова чисельність працівників) | |
| Р (у) (рентабельність продукції) | 0,87 | 0,65 | |
| ФЗоз (х1) (фондоозброєність основних засобів) | 0,87 | 0,36 | |
| Ч (х2) (середньоспискова чисельність працівників) | 0,65 | 0,36 |
Вирішення
1. Визначимо  -коефіцієнти для факторів х1 і х2 (формула 10.28):
-коефіцієнти для факторів х1 і х2 (формула 10.28):
 = 0,731
= 0,731
 = 0,387
= 0,387
2. Розрахуємо коефіцієнт множинної кореляції (формула 10.26):

 0,945
0,945
На наступному етапі аналізу перевіряється адекватність моделі за допомогою використанням F-критерію Фішера і t-критерію Ст’юдента. При перевірці на адекватність економетричної моделі також використовується тест Дарбіна-Уотсона, який спрямований для перевірки кореляції між залишками.
На останньому етапі отримана модель аналізується і інтерпретується.
Читайте також:
- CMM. Визначення моделі зрілості.
- III. GPSS — програма імітаційної моделі ЕОМ
- ISO 15504.Структура еталонної моделі
- Автокореляція залишків – це залежність між послідовними значеннями стохастичної складової моделі.
- Авторегресійні моделі в аналізі динаміки економічних процесів і їх прогнозуванні
- Аксіоматичний метод у математиці та суть аксіоматичної побудови теорії.
- Алгоритм побудови
- Алгоритм побудови калібрувального графіка для визначення загального білка сироватки крові
- Алгоритм побудови калібрувального графіка для визначення загального білка сироватки крові
- Алгоритм побудови організаційних структур управління.
- Алгоритм побудови сітьових графіків.
- Алгоритм реалізації моделі
| <== попередня сторінка | | | наступна сторінка ==> |
| Сутність кількісного регресійного аналізу | | | Критерії оцінки адекватності лінійної моделі множинної регресії |
|
Не знайшли потрібну інформацію? Скористайтесь пошуком google: |
© studopedia.com.ua При використанні або копіюванні матеріалів пряме посилання на сайт обов'язкове. |