
РЕЗОЛЮЦІЯ: Громадського обговорення навчальної програми статевого виховання
ЧОМУ ФОНД ОЛЕНИ ПІНЧУК І МОЗ УКРАЇНИ ПРОПАГУЮТЬ "СЕКСУАЛЬНІ УРОКИ"
ЕКЗИСТЕНЦІЙНО-ПСИХОЛОГІЧНІ ОСНОВИ ПОРУШЕННЯ СТАТЕВОЇ ІДЕНТИЧНОСТІ ПІДЛІТКІВ
Батьківський, громадянський рух в Україні закликає МОН зупинити тотальну сексуалізацію дітей і підлітків
Відкрите звернення Міністру освіти й науки України - Гриневич Лілії Михайлівні
Представництво українського жіноцтва в ООН: низький рівень культури спілкування в соціальних мережах
Гендерна антидискримінаційна експертиза може зробити нас моральними рабами
ЛІВИЙ МАРКСИЗМ У НОВИХ ПІДРУЧНИКАХ ДЛЯ ШКОЛЯРІВ
ВІДКРИТА ЗАЯВА на підтримку позиції Ганни Турчинової та права кожної людини на свободу думки, світогляду та вираження поглядів
- Гідрологія і Гідрометрія
- Господарське право
- Економіка будівництва
- Економіка природокористування
- Економічна теорія
- Земельне право
- Історія України
- Кримінально виконавче право
- Медична радіологія
- Методи аналізу
- Міжнародне приватне право
- Міжнародний маркетинг
- Основи екології
- Предмет Політологія
- Соціальне страхування
- Технічні засоби організації дорожнього руху
- Товарознавство продовольчих товарів
Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция
Авторегресійні моделі в аналізі динаміки економічних процесів і їх прогнозуванні
При оцінки динаміки економічних процесів і їх прогнозуванні необхідно спиратись на обґрунтовану теорію, що встановлює правомочність оцінки і прогнозування за допомогою моделі і помилки вірогідності прогнозу. Оцінка такої помилки за допомогою функції зростання неможлива, тому особливий інтерес представляють авторегресійні моделі.
Авторегресією називається рівняння, що визначає змінну хj в момент t (або t-й період) через її значення в попередні періоди: (t-1) (t-2)... (t-к). Лінійне авторегресійне рівняння записуємо у вигляді
Хt = а1 Хt-1 + а2 Хt-2 + + ак Хt-к. (12.17)
Першим етапом дослідження часового ряду змінної Х є виділення загальної тенденції у вигляді функції d(t) і визначення залишків εt у формі εt = Хt - d(t) чи εt = d(хt).
Якщо залишки εt незалежні, тобто не можуть бути представлені як функція часу, то функція d(t) охоплює повністю еволюційну складову змінної Хt. При цьому залишається знайти закон їх розподілу εt і, прийнявши гіпотезу про збереження цього закону розподілу на прогнозований період, побудувати довірчий інтервал для прогнозованої величини Хt за функцією d(t). Якщо ж залишки εt залежні, тобто містять деяку тенденцію, то її можна виявити за допомогою коефіцієнта автокореляції. Проводячи зсув значень εt на один рядок і останнє значення переміщаємо на перше місце, одержуємо табл. 12.9.
Таблиця 12.9. Залишки змінних ряду динаміки
| εt | εt-1 |
| ε1 | εn |
| ε2 | ε1 |
| ε3 | ε2 |
| ………… | ………….. |
| εn | εn-1 |
Обчислюємо циклічний коефіцієнт кореляції між рядами εt і εt-1 за формулою
r(εt, εt-1) = 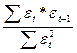 . (12.18)
. (12.18)
Ця формула (12.18) виходить із звичайної формули для визначення коефіцієнта кореляції, якщо покласти
∑ εt = ∑ εt-1 = 0; (12.19)
∑ (εt -1)2 = ∑ (εt)2 . (12.20)
Формула (12.19) виходить з того, що параметри функції d(t) визначаються за методом якнайменших квадратів, а формула (12.20) - з циклічної табл. 12.9.
Аналогічно, зсовуючи εt на 2,3….К рядків, одержуємо циклічну таблицю послідовних відхилень.
Таблиця 12.10. Циклічна таблиця послідовних відхилень
| t | εt | εt-1 | εt-2 | ……… | εt-к+1 | εt-к |
| ε1 | εn | εn-1 | εn-k+2 | εn-k+1 | ||
| ε2 | ε1 | εn | εn-k+3 | εn-k+2 | ||
| ε3 | ε2 | ε1 | εn-k+4 | εn-k+3 | ||
| …. | …. | …. | …. | …. | …. | |
| К | εk | εk-1 | εk-2 | ε1 | εn | |
| К+1 | εk+1 | εk | εk-1 | ε2 | ε1 | |
| К+2 | εk+2 | εk+1 | εk | ε3 | ε2 | |
| ….. | ….. | …. | …. | …. | …. | …. |
| n | εn | εn-1 | εn-2 | εn-k+1 | εn-k |
За даними табл. 12.10 визначаємо всі циклічні коефіцієнти автокореляції:
r(εxt εxt-j) = 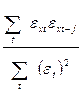 , i, j = 1,2,…..K; (12.21)
, i, j = 1,2,…..K; (12.21)
r(εxt-1 εxt-j) = 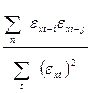 . (12.22)
. (12.22)
Циклічний коефіцієнт автокореляції не підпорядковується нормальному закону розподілу, його розподіл асиметричний, суттєві величини коефіцієнтів автокореляції при певному рівні значущості різні для позитивних і негативних його значень. 5% - й і 1% - й рівні значущості коефіцієнтів автокореляції подані в спеціальних таблицях. Знайдені значення r1, r2… rn-к-1 перевіряємо по таблиці 5% - х і 1% - х рівнів вірогідності коефіцієнтів автокореляції. Якщо | rстат. (n) | < | r5%. (n) |, то приймаємо гіпотезу неавтокорельованості залишків εt; якщо | rстат. (n) | > | r1%. (n) | відкидаємо гіпотезу їх неавтокорельованості.
За циклічними коефіцієнтами автокореляції складаємо матрицю і її обертаємо. Як і в разі звичайної регресії багаточинника, перевіряємо наявність мультиколінеарності кожного з чинників εxt-j, j=1,2-k від сукупності інших і зберігаємо тільки лінійно незалежні аргументи.
Будуємо лінійну авторегресійну модель
εt = а1 εt-1 + а1 εt-2 + ….+ ак εt-к, (12.23)
що виражає εt в період t за допомогою значень εt-j, j = 1,2…К за К попередніх періодів. При цьому в рівнянні повинні бути збережені тільки суттєві і лінійно незалежні коефіцієнти.
Якщо виявляються аj – коефіцієнти, що не задовольняють вказаним вимогам, то модель потребує перерахунку (починаючи з розрахунку автокореляційної матриці більш низького порядку).
Оскільки параметри рівняння тренда визначали за методом найменших квадратів, то в разі його коректного підбору відповідні відхилення підкоряються нормальному розподілу, і, отже, рівняння регресії можна відшукувати в лінійній формі
ℓn Xt = a1 ℓn Xt-1 + a2 ℓn Xt-2 +…….+ak ℓn Xt-k + F(t); (12.24)
Xt = a1 Xt-1 + a2 ℓn Xt-2 +……..+ an Xt-k + F(t). (12.25)
Яким повинне бути число членів рівняння, це питання слід вирішувати в поєднанні професійних вимог процесу, що по суті вивчається, з математико-статистичними критеріями. Так, якщо статистичний ряд містить тижневі дані, то особливий інтерес являє чотиричленна модель залежності рівня показника від тижневих рівнів за весь попередній місяць. У разі місячних даних цікава тричленна авторегресія, а для даних, зібраних по роках, – п’ятичленна.
Статистичні критерії покликані встановити відсутність автокорельованості залишків від віднімання з табличних значень εt їх розрахункових значень
ηt = εt – (a1 εt-1 + a2 εt-2 +…+ ak εt-2k) . (12.26)
Існує декілька статистичних критеріїв. Один з них заснований на порівнянні середнього квадрата послідовних різниць ηt:

 . (12.27)
. (12.27)
З дисперсією величини
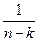
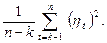 (12.28)
(12.28)
Складаємо відношення середнього квадрата послідовних різниць, до середнього квадрата самих величин:
К = 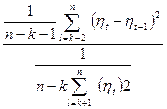 . (12.29)
. (12.29)
Якщо Кстат., потрапляє в допустиму область при рівні значущості 5%, а саме К5% (n-k) < Кстат (n-k) < К15% (n-k), то приймаємо гіпотезу неавтокорельованості залишків ηt, а, отже, і достатності числа членів К авторегресійної моделі.
Якщо ж Кстат (n-k) < К% (n-k) або Кстат > К1% (n-k), то відкидаємо гіпотезу неавтокорельованості залишків ηt і рахуємо число членів рівняння недостатності. У цьому випадку число членів рівняння треба збільшити, якщо довжина ряду дозволяє це.
Користуючись для прогнозу розробленими рівняннями, можна знайти довірчий інтервал для значення прогнозованого показника.
Якщо прогнозований показник рівний 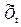 , то розмір показника Хt записуємо у вигляді
, то розмір показника Хt записуємо у вигляді
 -
-  ≤ Xt ≤ +
≤ Xt ≤ +  . (12.30)
. (12.30)
Викладена методика складання авторегресійних моделей, використані критерії і побудований довірчий інтервал можна застосовувати тільки для великих вибірок, коли довжина ряду n не менше 30.
Помилка прогнозу по отриманих рівняннях визначається за дисперсії εt. Оскільки
 - Хt = εt, (12.31)
- Хt = εt, (12.31)
то Βер 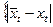 = | εt| ≤ tα σε
= | εt| ≤ tα σε  = Pα, (12.32)
= Pα, (12.32)
де Pα – задана вірогідність, Pα = 1-α, а tα - відповідна межа по С (n-k) ступеням свободи Стьюдента:
σε = 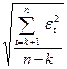 . (12.33)
. (12.33)
Розглянемо приклади складання авторегресійних моделей.
Одночленна модель. Щомісячний пробіг рухомого складу міського електротранспорту на 1000 пасажирів, що перевозяться, заданий рядом в графі 2 табл. 12.11. Знайдіть параметри одночленної авторегресійної моделі і спрогнозуйте щомісячний пробіг рухомого складу міського електротранспорту.
Вирішення
Наявність експоненціального ряду (див. рис. 12.3.) дозволяє розраховувати на придатність одночленної моделі  = а1Хt-1.
= а1Хt-1.
Система нормальних рівнянь для визначення параметра а1 має вигляд
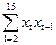 = а1
= а1 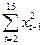 . (12.34)
. (12.34)
З табл. 12.11. (графи 4 і 5) виходить 367673,4 = 364278,2 а1
Звідки а1 =  = 1,0087 ≈ 1,01.
= 1,0087 ≈ 1,01.
Одержуємо рівняння  = 1,01 Хt-1. Обчислюємо значення
= 1,01 Хt-1. Обчислюємо значення  = 1,01 Хt-1 (графа 6) і знаходимо значення εt = Xt -Хt-1 (графа 7) ∑ εt = 9,4, що несуттєво в порівнянні з розмірами Xt.
= 1,01 Хt-1 (графа 6) і знаходимо значення εt = Xt -Хt-1 (графа 7) ∑ εt = 9,4, що несуттєво в порівнянні з розмірами Xt.
Обчислюємо коефіцієнт циклічної автокореляції r1. За графами 9 і 10 отримаємо
r1 = r(εt, εt-1) = 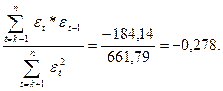 (12.35)
(12.35)
З табл. 12.11 знаходимо n1 = 15-1=14, r<0, r5% = -0,479.
Оскільки | r1| < | r5%|, кореляція εt, εt-1 несуттєва.
Аналогічно за графами 12 і 10 (табл. 12.11) одержуємо r2 =  = 0,416, що свідчить про несуттєвість кореляції εt и εt-2.
= 0,416, що свідчить про несуттєвість кореляції εt и εt-2.
У даному випадку переважний критерій Дж. Неймана. Обчислюємо різницю εt -εt-1 за графами 13 і (εt -εt-1)2 – за графами 14. Одержуємо
K= 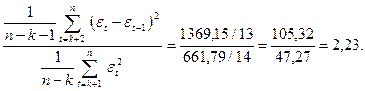 (12.36)
(12.36)
За табл. 12.11 для n1 = 14 рівень значущості К5% рівний 1,2725 при r > 0 і 3,0352 у разі r < 0. Розрахунки свідчать, що коли в генеральній сукупності автокореляція між залишками εt відсутня, то в 95% вибірок буде К > 1,272 у випадку r > 0 и К < 3,0352 при <.
У даному прикладі значення К потрапляє в допустиму область при 5% рівні значущості К > 1,2725. Отже, гіпотеза неавтокорельованості залишків εt стверджується і авторегресійне рівняння Xt = 1,01 Xt-1 приймається.
Помилка прогнозу при середньоквадратичному відхиленні
σε = 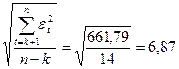 . (12.37)
. (12.37)
Складаємо
Вср = 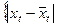 ≤ tα *
≤ tα *  = Pa . (12.38)
= Pa . (12.38)
При 95%-й гарантійної вірогідності tα = 2,1 за табл. П.4[12] і помилка прогнозу не перевищить 14,42, що складає приблизно 8%:
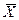 - 14,42 ≤ 1,01 Xt-1 ≤
- 14,42 ≤ 1,01 Xt-1 ≤ 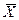 + 14,42 (12.39)
+ 14,42 (12.39)
Визначаємо прогноз на 16-й і 17-й періоди з похибкою, що не перевершує 14,42 (рис. 12.3.):
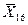 = 1,01 * Х15 = 1,01 * 175,3 = 177,05; (12.40)
= 1,01 * Х15 = 1,01 * 175,3 = 177,05; (12.40)
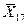 = 1,01 Х17 = 1,01 * 175,5 = 177,06. (12.41)
= 1,01 Х17 = 1,01 * 175,5 = 177,06. (12.41)
Таблиця 12.11. Розрахунок параметрів одночленної авторегресійної моделі
| t | Xt | Xt-1 | Xt Xt-1 | Xt-12 | 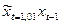
| εt= Xt- 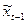
| εt-1 | εt* εt-1 | εt2 | εt-2 | еt* еt-2 | еt - еt-1 | (еt - еt-1)2 |
| 153,1 | - | - | - | - | - | - | - | - | - | - | - | - | |
| 153,3 | 153,1 | 23470,2 | 23439,6 | 154,6 | -1,3 | 5,4 | -7,02 | 1,69 | 1,7 | 2,21 | 5,1 | 26,01 | |
| 148,4 | 153,3 | 22749,7 | 23500,9 | 154,8 | -6,4 | -1,3 | 8,32 | 40,96 | 5,4 | -34,56 | -5,4 | 29,16 | |
| 148,9 | 148,4 | 22096,8 | 22026,6 | 149,9 | -1,0 | -6,4 | 6,4 | 1,0 | -1,3 | 1,3 | -11,0 | 14,0 | |
| 160,4 | 148,9 | 23883,6 | 22171,2 | 150,4 | 1,0 | 10,0 | 1,0 | -6,4 | -64,6 | 11,5 | 132,25 | ||
| 160,5 | 160,4 | 25744,2 | 25728,2 | 162,0 | -1,5 | 10,0 | -15,0 | 2,25 | -1,0 | 1,5 | 10,89 | ||
| 157,3 | 160,5 | 25246,6 | 25760,2 | 162,1 | -4,8 | -1,5 | 7,2 | 23,04 | 10,0 | -48,0 | -16,5 | 272,25 | |
| 170,6 | 157,3 | 26835,4 | 24743,3 | 158,9 | 11,7 | -4,8 | -16,5 | 136,89 | -1,5 | -17,55 | 3,3 | 10,89 | |
| 163,9 | 170,6 | 27961,3 | 29104,4 | 172,3 | -8,4 | 11,7 | -98,27 | 70,56 | -4,8 | 40,32 | -7,4 | 54,76 | |
| 164,3 | 163,9 | 26928,3 | 26863,2 | 165,3 | -1,0 | -8,4 | 8,4 | 1,0 | 11,7 | -11,7 | -16,1 | 259,21 | |
| 170,9 | 164,3 | 28078,9 | 26994,5 | 155,8 | 15,1 | 1,0 | 15,1 | 228,01 | -8,4 | -126,84 | 19,8 | 292,04 | |
| 167,9 | 170,9 | 28694,1 | 29206,8 | 172,6 | -4,7 | 15,1 | -70,97 | 22,09 | -1,0 | 4,7 | -3,2 | 10,24 | |
| 168,1 | 167,9 | 28223,9 | 28190,4 | 169,6 | -1,5 | -4,7 | 7,05 | 2,25 | 15,1 | -22,65 | 0,2 | 0,04 | |
| 168,2 | 168,1 | 28274,4 | 28257,6 | 169,9 | -1,7 | -1,5 | 2,55 | 2,89 | -4,7 | 7,99 | -7,1 | 50,41 | |
| 175,3 | 168,2 | 29485,5 | 28291,2 | 169,9 | 5,4 | -1,7 | 9,18 | 29,16 | -1,5 | -8,4 | - | - | |
| 175,5 | 367673,4 | 364278,2 | 9,4 | -184,64 | 661,179 | -275,68 | 1369,15 |

Рис. 12.3. Одночленна авторегресійна модель:
1-вихідні дані; 2-одночленна авторегресія; 3-вирівнююча гіпербола.
Багаточленна модель. Щомісячна реалізація цегли (в тисячах штук) на базі будівельних матеріалів за 18 місяців представлена в табл. 12.12 (графа 2). Треба скласти модель для прогнозування місячної потреби в цеглі на найближчі місяці.
Вирішення
Розрахунок багаточленної авторегресійної моделі представимо в табл. 12.12.
| Xt | Xt-1 | 
| εt=Xt-Xt-1 | εt-1 | εt*εt-1 | εt2 | εt-εt-1 | (εt-εt-1)2 | Xt-2 | ||
| - | - | - | - | - | - | - | - | - | ||||
| 16,55 | 0,55 | 2,84 | -1,5 | 0,3 | - | - | - | |||||
| 18,75 | 4,25 | 0,55 | 2,34 | 18,06 | -3,7 | 13,68 | ||||||
| 25,37 | 1,63 | 4,25 | 6,93 | 2,66 | 2,62 | 6,86 | ||||||
| 29,78 | 2,22 | 1,63 | 3,62 | 4,92 | -0,59 | 0,35 | ||||||
| 35,29 | -6,29 | 2,22 | -20,6 | 86,3 | 11,51 | 132,48 | ||||||
| 28,68 | -7,68 | -9,29 | 71,35 | 58,98 | 1,61 | 2,59 | ||||||
| 23,16 | -5,16 | -7,68 | 39,63 | 26,63 | -2,62 | 6,35 | ||||||
| 19,55 | -4,55 | -5,16 | 23,48 | 20,70 | -0,61 | 0,37 | ||||||
| 16,55 | 2,45 | -4,55 | -11,15 | 6,00 | 7,0 | |||||||
| 20,96 | 3,04 | 2,45 | 7,45 | 9,24 | -0,59 | 0,35 | ||||||
| 26,47 | 6,53 | 3,04 | 19,85 | 42,64 | -3,49 | 12,18 | ||||||
| 36,40 | 0,6 | 6,53 | 3,92 | 0,36 | 6,47 | 41,86 | ||||||
| 40,81 | 0,19 | 0,6 | 0,11 | 0,36 | 0,41 | 1,68 | ||||||
| 45,22 | -1,78 | 0,19 | -0,34 | 3,17 | 1,97 | 3,88 | ||||||
| 47,43 | -2,43 | -1,78 | 4,33 | 5,9 | 0,75 | 0,56 | ||||||
| 49,64 | -2,64 | -2,43 | 6,42 | 6,97 | 0,21 | 0,04 | ||||||
| 51,24 | -2,84 | -2,64 | 7,5 | 8,07 | 0,2 | 0,04 | ||||||
| ∑ | 162,28 | 301,26 | 272,2 |
Продовження табл. 12.12
| Xt*Xt-1 | Xt*Xt-2 | Xt-1* Xt-2 | Xt-12 | X 2t-2 | 0,1175 Xt-1 | 1,061 Xt-2 | 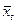
| εt=Xt- 
| εt2 | εt- εt-1 | (εt- εt-1)2 |
| - | - | - | - | - | - | - | - | - | - | - | - |
| - | - | - | - | - | - | - | - | - | - | - | - |
| 1,99 | 15,91 | 17,9 | 5,1 | 26,01 | - | - | |||||
| 2,70 | 18,04 | 20,74 | 6,26 | 39,8 | -1,13 | 1,27 | |||||
| 3,17 | 24,40 | 27,57 | 4,43 | 19,62 | 1,83 | 3,35 | |||||
| 3,76 | 28,64 | 32,30 | -6,3 | 39,69 | 10,73 | 115,13 | |||||
| 3,05 | 33,95 | 37,00 | -16,0 | 25,6 | 9,7 | 94,09 | |||||
| 2,46 | 27,58 | 30,04 | -12,04 | 144,96 | -3,96 | 15,68 | |||||
| 2,11 | 22,28 | 24,38 | -9,38 | 86,49 | -2,66 | 7,07 | |||||
| 1,76 | 19,09 | 20,85 | -1,85 | 3,42 | -7,52 | 56,55 | |||||
| 2,23 | 15,92 | 18,15 | 5,95 | 35,4 | -7,80 | 60,84 | |||||
| 2,82 | 25,46 | 22,98 | 10,02 | 100,4 | -4,07 | 16,54 | |||||
| 3,87 | 26,52 | 29,33 | 7,67 | 58,82 | 2,35 | 5,52 | |||||
| 4,34 | 33,20 | 37,54 | 3,46 | 11,97 | 4,21 | 17,72 | |||||
| 4,82 | 39,25 | 44,07 | -1,07 | 1,14 | 4,53 | 20,52 | |||||
| 5,05 | 43,50 | 48,55 | -3,55 | 12,6 | -2,48 | 6,15 | |||||
| 5,29 | 45,62 | 50,91 | -3,91 | 15,29 | 0,36 | 0,12 | |||||
| 5,52 | 47,74 | 52,26 | -4,26 | 18,14 | 0,35 | 0,12 | |||||
| 15,47 | 428,33 |
Використовуючи перші 18 членів ряду, складемо одночленну модель  = а1 Хt-1. Визначаємо а1 за методом середніх (табл. 12.12, графи 2.3):
= а1 Хt-1. Визначаємо а1 за методом середніх (табл. 12.12, графи 2.3):
а = 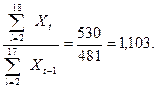 (12.42)
(12.42)
Обчислюємо значення  = 1,103 Хt-1 і залишків εt =
= 1,103 Хt-1 і залишків εt =  - Хt (графи 4, 5). Для використання першого критерію автокорельованості складаємо циклічний ряд εt-1 (графа 6), обчислюємо εt * εt-1 (графа 7) і εt2 (графа 8). У результаті одержуємо
- Хt (графи 4, 5). Для використання першого критерію автокорельованості складаємо циклічний ряд εt-1 (графа 6), обчислюємо εt * εt-1 (графа 7) і εt2 (графа 8). У результаті одержуємо
r1 = r(εt, εt-1) = 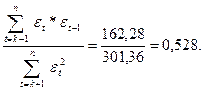 (12.43)
(12.43)
За табл. 12.12 знаходимо n1 = 18 – 1 =17 і r > 0, маємо r1% = 0,475.
Отже, r1 потрапляє в критичну область при 1% рівні значущості, що дає підставу відкинути гіпотезу неавтокорельованості εt.
Таким чином, модель  = а1 Хt-1 не приймається. До такого ж висновку приводить і другий критерій Дж. Неймана. На підставі граф 8,10 отримаємо
= а1 Хt-1 не приймається. До такого ж висновку приводить і другий критерій Дж. Неймана. На підставі граф 8,10 отримаємо
К =  (12.44)
(12.44)
За табл. 12.12 знаходимо: n1 = 17 маємо К1% = 1,035. Значить, К потрапляє в критичну область при 1% рівні значущості, що дає підставу забракувати гіпотезу відсутності автокорельованості εt.
Складаємо двочленну модель 
 = а1 Хt-1. + а2Хt-2. Система нормальних рівнянь для визначення параметрів методом якнайменших квадратів має видгляд:
= а1 Хt-1. + а2Хt-2. Система нормальних рівнянь для визначення параметрів методом якнайменших квадратів має видгляд:
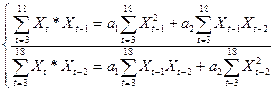 . (12.45)
. (12.45)
Визначивши суми для вирішення системи (табл. 12.12, графи 12-16), отримаємо 16289=1728 а1 + 14241 а2 ; 14853 = 14241 а1 + 13187 а2, звідки а1 = 0,1175; а2 = 1,061. У графах 17-19 наведені значення Хt, розраховані по формулі  = 0,1175 Хt-1 + 1,061 Хt-2 . Відхилення εt знаходимо за графами 20 і критерієм Дж. Неймана перевіряємо неавтокорельованість залишків. З граф 21,23
= 0,1175 Хt-1 + 1,061 Хt-2 . Відхилення εt знаходимо за графами 20 і критерієм Дж. Неймана перевіряємо неавтокорельованість залишків. З граф 21,23
K= 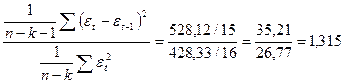 . (12.46)
. (12.46)
За табл. 12.12 маємо:
К5% (16) = 1,309 при r > 0;
К5% (16) = 2,9577 при r < 0.
Отже, розрахункове значення К потрапляє в допустиму область при 5% рівні значущості, що дає підставу для ухвалення гіпотези неавтокорельованості залишків εt для затвердження двочленній моделі:  = 0,1175 Хt-1 + 1,061 Хt-2. При середньоквадратичному відхиленні
= 0,1175 Хt-1 + 1,061 Хt-2. При середньоквадратичному відхиленні
σε = 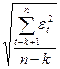 =
= 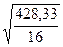 = 5,17 (12.47)
= 5,17 (12.47)
помилка прогнозу Вср =  ≤ tα *
≤ tα * 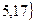 = Pα; при 90%-й гарантійної вірогідності tα = 1,74 помилка прогнозу не перевищить 8,84.
= Pα; при 90%-й гарантійної вірогідності tα = 1,74 помилка прогнозу не перевищить 8,84.
Прогноз на 19 і 20 періоди Х19 = 55,61; Х20 = 58,20 з 90%-й вірогідністю непереходу за межі
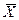 - 8,84 ≤ 0,1175 Хt-1 + 1,061 Хt-2 ≤
- 8,84 ≤ 0,1175 Хt-1 + 1,061 Хt-2 ≤ 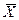 + 8,84. (12.48)
+ 8,84. (12.48)
Таким чином, представлені методики оцінки динаміки економічних процесів і розробки відповідних економетричних моделей динаміки дають змогу приймати управлінські рішення з урахуванням періодів функціонування підприємства та прогнозування економічних показників.
Питання і завдання для самоконтролю до змістового модулю 5
Питання для самоконтролю:
1. Назвіть основні принципи при побудові економетричних моделей?
2. Охарактеризуйте основні критерії оцінки адекватності економетричних моделей?
3. Що таке мультиколінеарність? Назвіть причини її виникнення.
4. В чому полягає парний регресійний аналіз?
5. В чому полягає кількісний регресійний аналіз? Який вигляд має кількісна регресійна модель?
6. Охарактеризуйте етапи побудови багатофакторної економетричної моделі?
7. Охарактеризуйте t-критерій Ст’юдента і F-критерій Фішера для оцінки адекватності багатофакторної економетричної моделі.
8. Охарактеризуйте тест Дарбіна-Уотсона для оцінки адекватності багатофакторної економетричної моделі.
9. Проінтепретуйте отримані результати на основі розробленої Вами багатофакторної економетричної моделі.
10. Охарактеризуйте узагальнені економетричні моделі.
11. Назвіть види узагальнених економетричних моделей і охарактеризуйте їх.
12. Назвіть основні поняття і визначте сутність динамічних процесів в економіці.
13. Що таке часовий ряд і назвіть напрями його оцінки.
14. Що таке авторегресія і як будуються авторегресійні моделі.
15. Назвіть статистичні критерії оцінки автокорельованості залишків і як вони визначаються.
Завдання для самоконтролю:
1. За статистичними даними 10 підприємств розробити рівняння регресії рівня витрат на виробництво продукції (Рввп) від фондоозброєності праці робітників (ФЗп):
1) побудувати поле кореляції і за ним визначити характер та обґрунтувати математичну форму рівняння регресії;
2) визначити коефіцієнти регресії а0 та а1, їх економічний зміст, записати рівняння регресії;
3) визначити коефіцієнти кореляції;
4) визначити з ймовірністю 0,95 довірчі границі помилки апроксимації, записати рівняння регресії в остаточному вигляді;
5) обґрунтувати економічну сутність отриманих результатів.
Таблиця 12.13. Статистичні дані діяльності підприємств
| № з/п | Рввп, коп./грн. | ФЗп, тис.грн./чол. |
| 91,7 | 1,9 | |
| 91,2 | 2,1 | |
| 87,7 | 5,4 | |
| 89,2 | 2,7 | |
| 90,2 | 2,2 | |
| 88,8 | 2,9 | |
| 91,7 | 2,6 | |
| 92,8 | 2,7 | |
| 85,7 | 6,3 | |
| 91,1 | 4,6 |
2. За статистичними даними 10 підприємств розробити рівняння регресії рівня витрат на виробництво продукції (Рввп) від фондовіддачи основних засобів (ФФоз):
1) побудувати поле кореляції і за ним визначити характер та обґрунтувати математичну форму рівняння регресії;
2) визначити коефіцієнти регресії а0 та а1, їх економічний зміст, записати рівняння регресії;
3) визначити коефіцієнти кореляції;
4) визначити з ймовірністю 0,95 довірчі границі помилки апроксимації, записати рівняння регресії в остаточному вигляді;
5) обґрунтування економічної сутності отриманих результатів.
Таблиця 12.14. Статистичні дані діяльності підприємств
| № з/п | Рввп, коп./грн. | ФФоз, тис. грн./тис. грн. |
| 91,7 | 12,9 | |
| 91,2 | 12,6 | |
| 87,7 | 11,9 | |
| 89,2 | 12,3 | |
| 90,2 | 12,4 | |
| 88,8 | 11,6 | |
| 91,7 | 12,7 | |
| 92,8 | 12,9 | |
| 85,7 | 11,2 | |
| 91,1 | 12,8 |
3. За статистичними даними 10 підприємств розробити рівняння регресії рентабельності реалізації продукції (Ррп) від коефіцієнту вибуття робітників (Квр):
1) побудувати поле кореляції і за ним визначити характер та обґрунтувати математичну форму рівняння регресії;
2) визначити коефіцієнти регресії а0 та а1, їх економічний зміст, записати рівняння регресії;
3) визначити коефіцієнти кореляції;
4) визначити з ймовірністю 0,95 довірчі границі помилки апроксимації, записати рівняння регресії в остаточному вигляді;
5) обґрунтування економічної сутності отриманих результатів.
Таблиця 12.15. Статистичні дані діяльності підприємств
| № з/п | Ррп, коп./грн. | Квр, % |
| 4,3 | 4,1 | |
| 4,8 | 3,3 | |
| 5,3 | 3,5 | |
| 6,8 | 2,8 | |
| 5,5 | 3,9 | |
| 5,2 | 3,6 | |
| 6,3 | 2,9 | |
| 7,2 | 2,7 | |
| 6,4 | 2,9 | |
| 7,9 | 2,1 |
4. Представлені статистичні дані собівартості пасажироперевезень міським електричним транспортом, (табл. 12.16), вирівняти за ковзаною середньою і побудувати графік і обґрунтувати тенденції зміни собівартості пасажироперевезень.
Таблиця 12.16. Статистичні дані собівартості пасажироперевезень по депо
| t | Собівартість С, коп |
| 89,9 | |
| 90,9 | |
| 87,6 | |
| 87,5 | |
| 88,2 | |
| 89,9 | |
| 90,5 |
Продовження табл. 12.16
| 92,8 | |
| 92,1 | |
| 92,8 | |
| 91,8 | |
| 93,1 |
5. На основі даних динаміки статистичних показників представлених в табл. 12.17 виявіть загальну тенденцію їх зміни, побудуйте економетричну модель динаміки і розрахуйте прогноз на 2 наступних роки.
Таблиця 12.17. Динаміка статистичних показників
| Роки | t | Значення показника, С, коп. | Квартал | ||||
| I | II | III | IV | ||||
| 68,59 | 72,4 | 65,88 | 69,53 | 66,54 | |||
| 69,95 | 72,8 | 67,34 | 71,21 | 68,44 | |||
| 75,37 | 74,53 | 77,49 | 72,88 | 76,59 | |||
| 75,49 | 79,22 | 73,21 | 73,34 | 76,19 | |||
| 82,34 | 77,34 | 82,29 | 85,45 | 87,29 | |||
| 91,80 | 88,92 | 90,72 | 93,19 | 94,39 | |||
6. Щомісячний пробіг рухомого складу міського електротранспорту на 1000 пасажирів, що перевозяться, представлений в табл. 12.18. Розрахуйте параметри авторегресійної моделі і складіть прогноз на наступні 2 місяці.
Таблиця 12.18. Щомісячний пробіг рухомого складу міського електротранспорту на 1000 пасажирів
| Період (t) | Щомісячний пробіг рухомого складу міського електротранспорту на 1000 пасажирів (Xt), км. |
| 167,1 | |
| 163,3 | |
| 168,4 | |
| 158,9 | |
| 160,4 |
Продовження табл. 12.18
| 160,5 | |
| 177,3 | |
| 171,6 | |
| 173,9 | |
| 174,2 | |
| 174,8 | |
| 171,3 | |
| 169,7 | |
| 170,2 | |
| 173,2 | |
| 185,5 |
7. Щомісячна реалізація покрівельних матеріалів (в тисячах штук) заводом за 18 місяців представлена в табл. 12.19. Треба скласти авторегресійну економетричну модель і спрогнозувати місячну потребу в покрівельних матеріалах на 2 наступні місяці.
Таблиця 12.19. Щомісячна реалізація покрівельних матеріалів (в тисячах штук) заводом
| Період (t) | Щомісячна реалізація покрівельних матеріалів (Xt), тис. штук |
Продовження табл. 2.19
Міністерство освіти і науки України
Харківська національна академія міського господарства
ПРИКЛАД
ТЕСТОВИХ ЗАВДАНЬ
Читайте також:
- CMM. Визначення моделі зрілості.
- CMM. Групи ключових процесів
- CMM: зрілість організацій і процесів
- H) інноваційний менеджмент – це сукупність організаційно-економічних методів управління всіма стадіями інноваційного процесу.
- III. GPSS — програма імітаційної моделі ЕОМ
- ISO 15504.Структура еталонної моделі
- S Визначення оптимального темпу роботи з урахуванням динаміки наростання втоми.
- Tема 4. Фації та формації в історико-геологічному аналізі
- VIІІ ЕКОНОМІКС МІЖНАРОДНИХ ЕКОНОМІЧНИХ ВІДНОСИН
- VІII. Основи молекулярної фізики і термодинаміки
- А) Показники, які використовують при аналізі кон'юнктури
- А) Структура економічних відносин.
| <== попередня сторінка | | | наступна сторінка ==> |
| Аналіз часових рядів економічних показників і побудова економетричних моделей динаміки | | | Альтернативні прості тест-завдання |
|
Не знайшли потрібну інформацію? Скористайтесь пошуком google: |
© studopedia.com.ua При використанні або копіюванні матеріалів пряме посилання на сайт обов'язкове. |