• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Гіпотези та припущення щодо властивостей та характеру деформацій.

Реальні матеріали мають різноманітні фізичні властивості й

характерну для кожного з них структуру. З метою спрощення розрахунків в опорі матеріалів використовуються наступні допущенняпро властивості матеріалу.

Матеріал вважається однорідним, тобто його властивості у всіх точках однакові.

Матеріал вважається ізотропним, тобто його властивості в усіх напрямках однакові.

Ізотропними є аморфні матеріали, такі як скло й смоли. Анізотропними є пластмаси, текстоліт і т.п. Метали є полікристалічними тілами, що складаються з великої кількості зерен, розміри яких дуже малі (порядку 0,01 мм). Кожне зерно є анізотропним, але внаслідок малих розмірів зерен і без порядного їх розташування метали проявляють властивість ізотропії.

Матеріал має властивість ідеальної пружності, внаслідок якого тіло, що деформується, повністю відновлює свою форму й розміри після зняття навантаження незалежно від величин навантажень і температури тіла.

Форма й розміри пружного тіла міняються прямо пропорційно зміні навантажень, тобто по відомому законуГука (1660 р.). У випадку чистого однорідного розтягання або стиску призматичного стрижня, законГука має вигляд:

де Р - розтягуюча (стискаюча) осьова сила;

l₀, F₀ - вихідна довжина й вихідна площа поперечного перерізу стрижня;

Е - фізична константа матеріалу - модуль поздовжньої пружності, різний для різних матеріалів;

Δl- абсолютне подовження розрахункової частини l₀ стрижнята

У формулюванні даної гіпотези границі застосування закону пропорційності Гука нічим не обмовляються, хоча в дійсності при деяких навантаженнях починається істотне відхилення від закону пропорційності.

У межах пружності має місце ефект Пуассона (1816 р.) - відношення відносних поперечних подовжень ε^’ до відносних поздовжніх подовжень ε є величина постійна для даного матеріалу:

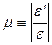або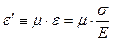

де μ- коефіцієнтПуассона - пружна константа матеріалів (0<μ<0.5).

Матеріал має властивість суцільності, тобто має здатність суцільно (без порожнеч) заповнювати простір, обмежений поверхнею тіла. Внаслідок цього матеріал уважається безперервним, що дозволяє використовувати для визначення напруг і деформацій математичний апарат диференціального й інтегрального вирахування.

Пружні тіла є відносно твердими, завдяки чому переміщення точок тіла досить малі в порівнянні з розмірами самого тіла. Ця гіпотеза служить підставою для принципу початкових розмірів.

Читайте також:

1. I. Дослідження фізичних властивостей
2. А) Визначення захисних властивостей, якими володіє сховище, за захисту від іонізуючого випромінювання.
3. Акцентуації характеру
4. Акцентуації характеру
5. АКЦЕНТУАЦІЯ ХАРАКТЕРУ
6. Акцентуація характеру – перебільшений розвиток певних властивостей характеру на шкоду іншим, в результаті чого погіршуються відносини з оточуючими людьми.
7. Аналіз властивостей радіоелектронних кіл
8. Анізотропія властивостей металів.
9. Блок 3.2. Лекція 9. Небезпеки техногенного характеру
10. В залежності від мети та характеру угоди, які лежать в основі випуску векселів, а також їх забезпечення розрізняють комерційні, фінансові та фіктивні векселя.
11. В залежності від обстановки та бойового завдання, наявності сил та засобів, а також від характеру місцевості, оборона може бути позиційною, маневреною .
12. В залежності від обстановки та бойового завдання, наявності сил та засобів, а також від характеру місцевості, оборона може бути позиційною, маневреною .

Переглядів: 667