
РЕЗОЛЮЦІЯ: Громадського обговорення навчальної програми статевого виховання
ЧОМУ ФОНД ОЛЕНИ ПІНЧУК І МОЗ УКРАЇНИ ПРОПАГУЮТЬ "СЕКСУАЛЬНІ УРОКИ"
ЕКЗИСТЕНЦІЙНО-ПСИХОЛОГІЧНІ ОСНОВИ ПОРУШЕННЯ СТАТЕВОЇ ІДЕНТИЧНОСТІ ПІДЛІТКІВ
Батьківський, громадянський рух в Україні закликає МОН зупинити тотальну сексуалізацію дітей і підлітків
Відкрите звернення Міністру освіти й науки України - Гриневич Лілії Михайлівні
Представництво українського жіноцтва в ООН: низький рівень культури спілкування в соціальних мережах
Гендерна антидискримінаційна експертиза може зробити нас моральними рабами
ЛІВИЙ МАРКСИЗМ У НОВИХ ПІДРУЧНИКАХ ДЛЯ ШКОЛЯРІВ
ВІДКРИТА ЗАЯВА на підтримку позиції Ганни Турчинової та права кожної людини на свободу думки, світогляду та вираження поглядів
- Гідрологія і Гідрометрія
- Господарське право
- Економіка будівництва
- Економіка природокористування
- Економічна теорія
- Земельне право
- Історія України
- Кримінально виконавче право
- Медична радіологія
- Методи аналізу
- Міжнародне приватне право
- Міжнародний маркетинг
- Основи екології
- Предмет Політологія
- Соціальне страхування
- Технічні засоби організації дорожнього руху
- Товарознавство продовольчих товарів
Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция
Диференціальне числення функції однієї змінної.
Основні теореми про границі
 ,
,
 ,
,
 .
.
Наслідки
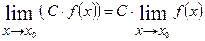 ,
,
 .
.
Перша важлива границя розкриває невизначеність  :
: 

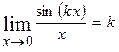 і
і 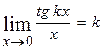 .
.
Друга важлива границя розкриває невизначеність  :
:  або
або 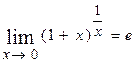

 і
і  .
.
Якщо  або
або  , то функцію
, то функцію  – називають нескінченно малою функцією.
– називають нескінченно малою функцією.
Еквівалентні нескінченно малі функції (  , коли
, коли 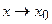 ):
):
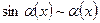
| 
|

| 
|

| 
|

| 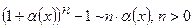
|
Існують односторонні границі функції: правостороння 
 і лівостороння
і лівостороння 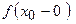
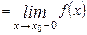 . Функція
. Функція 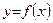 неперервна в точці
неперервна в точці  , якщовонавизначена в ній, односторонні границі в точці існують і рівні між собою. У противному випадку точка
, якщовонавизначена в ній, односторонні границі в точці існують і рівні між собою. У противному випадку точка  є точкою розриву. Маємо усувний розрив, якщо функція в точці невизначена, а границя функції в точці існує. Розрив першого роду, якщо функція в точці невизначена, односторонні границі існують, але не рівні між собою. В цьому випадку стрибок функції визначається формулою
є точкою розриву. Маємо усувний розрив, якщо функція в точці невизначена, а границя функції в точці існує. Розрив першого роду, якщо функція в точці невизначена, односторонні границі існують, але не рівні між собою. В цьому випадку стрибок функції визначається формулою  . Маємо розрив другого роду, якщо хоча б одна з односторонніх границь не існує або дорівнює нескінченності.
. Маємо розрив другого роду, якщо хоча б одна з односторонніх границь не існує або дорівнює нескінченності.
Правила диференціювання. Маємо функції  і
і  ,
,  t.
t.

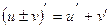

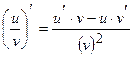
Таблиця похідних для функцій  .
.

| 
|

| 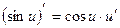
|
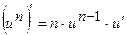
| 
|
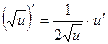
| 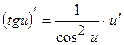
|

| 
|
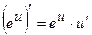
| 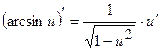
|

| 
|

| 
|
Для степенево-показникової функції  :
:
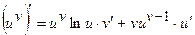
Для гіперболічних функцій:

| 
|

| 
|
Похідні мають вигляд:
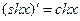
| 
|

| 
|
Функція 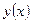 є неявно заданою, якщо рівняння
є неявно заданою, якщо рівняння 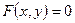 неможливо розв’язати відносно функції
неможливо розв’язати відносно функції 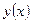 . При знаходженні похідної такої функції необхідно рівняння про диференціювати зліва направо, враховуючи, що
. При знаходженні похідної такої функції необхідно рівняння про диференціювати зліва направо, враховуючи, що 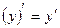 і
і  . Отримане рівняння розв’язують відносно
. Отримане рівняння розв’язують відносно  .
.
У деяких випадках при знаходженні похідної доцільно функцію спочатку прологарифмувати, а потім знайти похідну як від неявної функції (логарифмічне диференціювання).
Якщо функція параметрично задана  , то похідна знаходиться за формулою
, то похідна знаходиться за формулою  .
.
Диференціал функції  знаходиться за формулою:
знаходиться за формулою:  .
.
Враховуючи, що  є функцією, то її можна диференціювати. Дістанемо
є функцією, то її можна диференціювати. Дістанемо  і так далі:
і так далі:  .
.
Для знаходження другої похідної параметрично заданої функції застосовується формула:  , або
, або  .
.
Правило Лопіталя застосовують для розкриття невизначеностей. Наприклад, для 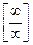 і
і  матимемо
матимемо 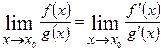 .
.
Диференціальне числення застосовують для дослідження функцій, знаходження найбільшого та найменшого значення функції на відрізку, знаходження рівнянь дотичної та нормалі до графіка функції в заданій точці.
Задача 16. Знайти область визначення D(y) функції
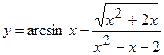
Розв’язання: Область визначення функції складається з обмежень для кожного доданку і утворює систему нерівностей:


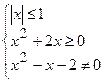 Þ
Þ 
 |
Розв’яжемо систему нерівностей методом інтервалів.
Розв’язок системи нерівностей: 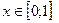 , тому
, тому  .
.
Задача 17.Знайти границі функції, не застосовуючи правило Лопіталя:
1)  при а)
при а) 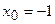 , б)
, б) 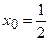 в)
в) 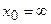
Розв’язання:
а) За умовою 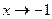 . Значення
. Значення 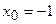 є граничним значенням змінної. Підставимо
є граничним значенням змінної. Підставимо 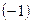 в чисельник і знаменник дробу замість
в чисельник і знаменник дробу замість 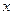 . Будемо мати для чисельника
. Будемо мати для чисельника 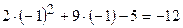 і для знаменника
і для знаменника  . Так як відношення отриманих значень є величина стала, то вона є границею:
. Так як відношення отриманих значень є величина стала, то вона є границею:
 ;
;
б) За умовою  . Значення
. Значення 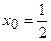 є граничним значенням змінної. Чисельник і знаменник дробу при цьому значенні дорівнюють нулю. Маємо невизначеність
є граничним значенням змінної. Чисельник і знаменник дробу при цьому значенні дорівнюють нулю. Маємо невизначеність  . Виконаємо наступні дії. Ділимо чисельник і знаменник дробу на
. Виконаємо наступні дії. Ділимо чисельник і знаменник дробу на  , тобто на
, тобто на  :
:
| 2x2+9x-5 | x- 1/2 | ||
| 2x2-x | 2x+10 | ||
| 10x-5 | |||
| 10x-5 | |||
| 6x2- x-1 | x- 1/2 | ||
| 6x2-3x | 6x+2 | ||
| 2x-1 | |||
| 2x-1 | |||
Переходимо до границі відношення часток від ділення. Матимемо

Зауваження. Замість ділення можна розкласти чисельник і знаменник на множники і зробити скорочення однакових виразів.
в) За умовою 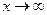 . Підставимо замість змінної
. Підставимо замість змінної  . Маємо невизначеність
. Маємо невизначеність 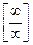 . Перетворимо дріб, поділивши його чисельник і знаменник на змінну в найвищому степені знаменника, тобто на
. Перетворимо дріб, поділивши його чисельник і знаменник на змінну в найвищому степені знаменника, тобто на  . Дістанемо:
. Дістанемо:
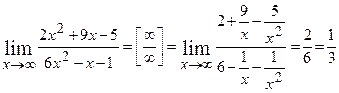
2) 
Розв’язання: Коли 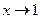 , то чисельник і знаменник дробу при цьому значенні дорівнюють нулю. Маємо невизначеність
, то чисельник і знаменник дробу при цьому значенні дорівнюють нулю. Маємо невизначеність  , якій сприяє ірраціональність. Позбавимось цієї ірраціональності. Для цього помножимо чисельник і знаменник на вираз, спряжений до
, якій сприяє ірраціональність. Позбавимось цієї ірраціональності. Для цього помножимо чисельник і знаменник на вираз, спряжений до 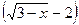 , тобто на
, тобто на  , а потім чисельник і знаменник поділимо на
, а потім чисельник і знаменник поділимо на  :
:

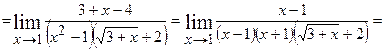
 .
.
3) 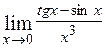 .
.
Розв’язання: При 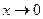 чисельник і знаменник дробу дорівнюють нулю. Маємо невизначеність
чисельник і знаменник дробу дорівнюють нулю. Маємо невизначеність  . Застосовуємо першу важливу границю. Оскільки
. Застосовуємо першу важливу границю. Оскільки 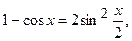 то
то

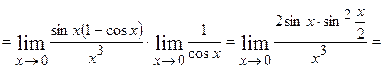
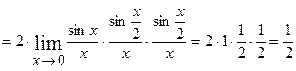 .
.
Зауваження. При розв’язуванні можна застосовувати таблицю еквівалентності нескінченно малих функцій.
4) 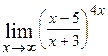
Розв’язання: При 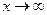 маємо невизначеність
маємо невизначеність  . Перетворимо під граничний вираз так, щоб можна було застосувати другу важливу границю. Поділимо чисельник на знаменник або виділимо в чисельнику вираз знаменника і перетворений чисельник поділимо на знаменник, щоб мати одним з доданків одиницю. Дістанемо:
. Перетворимо під граничний вираз так, щоб можна було застосувати другу важливу границю. Поділимо чисельник на знаменник або виділимо в чисельнику вираз знаменника і перетворений чисельник поділимо на знаменник, щоб мати одним з доданків одиницю. Дістанемо:

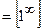
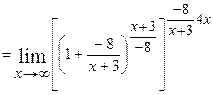 . Оскільки
. Оскільки 
 і
і 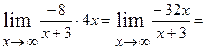
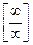 =
=
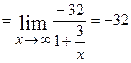 , то
, то 
Задача 18. Дослідити на неперервність функцію, установити характер точок розриву. Зробити схематичне креслення.
а)  .
.
Розв’язання: Оскільки дана функція показникова, то вона неперервна при всіх значеннях 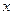 , крім
, крім 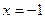 . В цій точці функція невизначена, тобто має в ній розрив. З¢ясуємо характер розриву.
. В цій точці функція невизначена, тобто має в ній розрив. З¢ясуємо характер розриву.
Знайдемо односторонні границі функції в точці 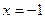 :
:


Оскільки одна з границь дорівнює  , то
, то 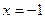 – точка розриву другого роду. Зробимо схематичне креслення
– точка розриву другого роду. Зробимо схематичне креслення

б) 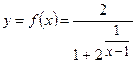
Розв’язання: Ця функція неперервна при всіх значеннях х, крім  . В цій точці вона невизначена. Точка
. В цій точці вона невизначена. Точка  є точкою розриву. З¢ясуємо характер розриву. Обчислимо односторонні границі функції в точці
є точкою розриву. З¢ясуємо характер розриву. Обчислимо односторонні границі функції в точці  .
.
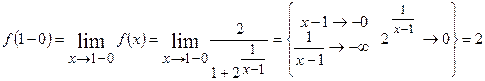
 Оскільки границі існують, але
Оскільки границі існують, але 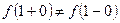 , маємо розрив першого роду. Стрибок
, маємо розрив першого роду. Стрибок  функції
функції 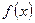 обчислюємо:
обчислюємо:
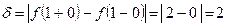 .
.  Зробимо схематичне креслення.
Зробимо схематичне креслення.
в) 

Розв’язання: Область визначення функції  . На інтервалах
. На інтервалах  ,
,  ,
,  функція неперервна. Розриви можуть бути лише в точках
функція неперервна. Розриви можуть бути лише в точках  і
і  . Обчислимо односторонні границі функції в точці
. Обчислимо односторонні границі функції в точці  :
:
 і
і  .
.
Оскільки  то в точці
то в точці  задана функція неперервна. Обчислимо односторонні границі функції в точці
задана функція неперервна. Обчислимо односторонні границі функції в точці  :
:
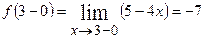 і
і  .
.
Так як  , то функція в точці
, то функція в точці  має розрив першого роду. Стрибок функції в точці розриву:
має розрив першого роду. Стрибок функції в точці розриву:

Зробимо схематичне креслення:
 |
Задача 19. Знайти похідні заданих функцій:
а) 
Розв’язання: 

=  .
.
б) 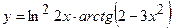
Розв’язання: 

 .
.
в) 
Розв’язання: 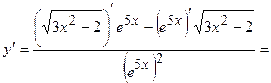
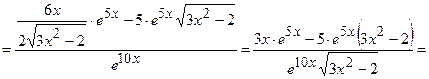
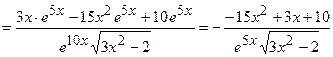 .
.
г) 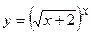
Розв’язання: Застосуємо логарифмічне диференціювання. Прологарифмуємо рівняння 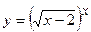 :
:  або
або  . При диференціюванні вважаємо, що
. При диференціюванні вважаємо, що  :
:
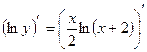

 ,
,



Враховуючи, що 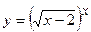 , матимемо:
, матимемо:

д) 
Розв’язання: Функція у неявно задана. Диференціюємо рівняння, вважаючи, що  .
.


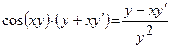
Виконаємо необхідні перетворення і розв’яжемо рівняння відносно  :
: 
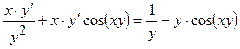 ;
;
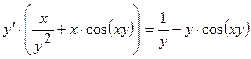 ;
;

Таким чином,  .
.
Задача 20. Знайти першу і другу похідні заданих функцій.
а) 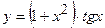
Розв’язання: Знайдемо  , а потім
, а потім  :
:

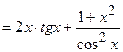 ;
;
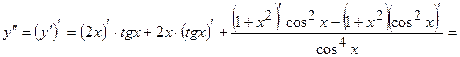


б) Знайти похідні параметрично заданих функцій. Застосуємо наведені вище формули.
1) 
Розв’язання: Знайдемо  і
і 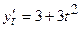 . Матимемо
. Матимемо  . Знайдемо
. Знайдемо  і
і 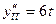 . Тоді друга похідна
. Тоді друга похідна 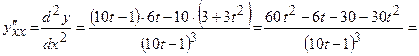
 .
.
2) 
Розв’язання: Знайдемо  ,
,
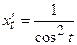 . Тоді перша похідна
. Тоді перша похідна 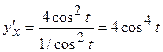 . Знайдемо
. Знайдемо  . Друга похідна функції визначається формулою
. Друга похідна функції визначається формулою  .
.
Задача 21. Знайти границю, застосувавши правило Лопіталя.

Розв’язання: Маємо невизначеність вигляду  . Зведемо цю невизначеність до вигляду
. Зведемо цю невизначеність до вигляду  ( приведемо до спільного знаменника), а потім застосуємо правило Лопіталя:
( приведемо до спільного знаменника), а потім застосуємо правило Лопіталя:



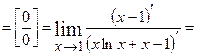
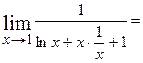
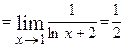 .
.
Задача 22.Знайти рівняння дотичної до графіка функції  в точці перетину його з віссю абсцис та рівняння нормалі в точці перетину його з віссю ординат.
в точці перетину його з віссю абсцис та рівняння нормалі в точці перетину його з віссю ординат.
Розв’язання: Знайдемо точки перетину графіка функції з осями координат:
а) з віссю  :
:  Þ
Þ  ;
; 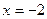 Þ
Þ 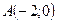 ;
;
б) з віссю  :
: 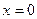 Þ
Þ  ; Þ
; Þ 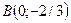 .
.
Знайдемо 
 . Обчислимо похідну в точках
. Обчислимо похідну в точках  і
і  :
:
 ,
, 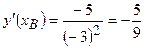
Запишемо рівняння дотичної в точці  :
:
 Þ
Þ 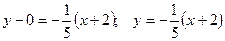 .
.
Запишемо рівняння нормалі в точці  :
:
 Þ
Þ  .
.
Задача 23. Знайти найбільше і найменше значення функції 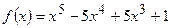 на відрізку
на відрізку  .
.
Розв’язання: Функція на відрізку неперервна. Знаходимо критичні точки, які належать даному відрізку. Перша похідна
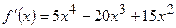 , звідки
, звідки 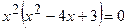 . Корені цього рівняння:
. Корені цього рівняння:  ,
, 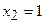 ,
,  .
. 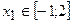 ;
;  ;
; 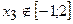 . Знайдемо значення функції в критичних точках
. Знайдемо значення функції в критичних точках 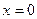 та
та  і на кінцях відрізка при
і на кінцях відрізка при 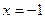 і
і  :
:
 .
.
Виберемо серед цих значень найбільше та найменше. Отже, 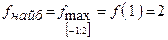 і
і 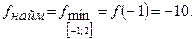
Задача 24.Дослідити за допомогою диференціального числення функцію  та побудувати її графік.
та побудувати її графік.
Розв’язання:
1. Область визначення функції : 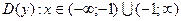
2. Точки перетину графіка функції з осями координат: з віссю  :
:  Þ
Þ 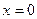 ; з віссю
; з віссю  :
: 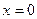 Þ
Þ  .
.
3. Перевіряємо виконання однієї із рівностей: якщо  то функція парна, якщо
то функція парна, якщо  то функція непарна. Жодна з
то функція непарна. Жодна з
рівностей не виконується, тому функція є ні парна, ні непарна. Графік функції не буде мати ніякої симетрії.
4. Знайдемо асимптоти графіка функції. Асимптоти можуть бути вертикальні і похилі.
В точці 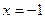 функція має нескінчений розрив
функція має нескінчений розрив
 і
і 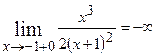 . Отже
. Отже 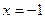 – рівняння вертикальної асимптоти.
– рівняння вертикальної асимптоти.
Знаходимо похилі асимптоти  , де
, де
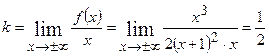 і
і

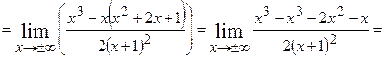
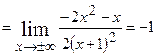 . Маємо рівняння похилої асимптоти
. Маємо рівняння похилої асимптоти  .
.
5. Знайдемо екстремум функції та інтервали зростання і спадання.
Перша похідна
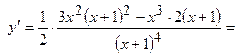

 . Знайдемо критичні точки:
. Знайдемо критичні точки: 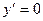 при
при  Þ
Þ  і
і  ,
,  не існує при
не існує при  Þ
Þ 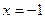 , але ця точка не належить області визначення. Складемо таблицю
, але ця точка не належить області визначення. Складемо таблицю
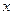
| 
| 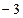
| 
| 
| 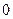
| 
|
 ¢ ¢
| 
| 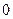
| 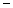
| 
| 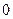
| 
|
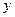
| зростає | mах | спадає | зростає | еxtr немає | зростає |
Знаходимо знак похідної  в кожному із інтервалів і результат занесемо в таблицю.
в кожному із інтервалів і результат занесемо в таблицю.

6 Знайдемо точки перегину, інтервали опуклості та вгнутості.
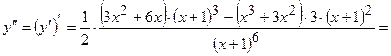

 . Знайдемо критичні точки:
. Знайдемо критичні точки:  при
при 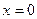 ;
;  не існує при
не існує при 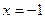 , але ця точка не належить області визначення. Складемо таблицю
, але ця точка не належить області визначення. Складемо таблицю
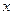
| 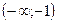
| 
| 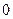
| 
|

| 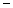
| 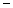
| 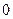
| 
|
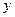
| 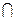
| 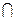
| перегин | 
|
Знаходимо знак похідної  в кожному з інтервалів і результат занесемо в таблицю. Значення функції в точці перегину
в кожному з інтервалів і результат занесемо в таблицю. Значення функції в точці перегину  .
.
Використовуючи одержані дані, будуємо графік функції.
 |
Читайте також:
- А. Це наявність в однієї людини кількох ліній клітин з різним набором хромосом.
- Автододавання та автообчислення.
- Автоматизоване робоче місце (АРМ) бухгалтера: призначення, функції та його рівні
- Адвокатура в Україні: основні завдання і функції
- Адміністративна відповідальність: поняття, мета, функції, принципи та ознаки.
- Алг W2 (ОБЧИСЛЕННЯ Y)
- Алгоритм знаходження ДДНФ (ДКНФ) для даної булевої функції
- Алгоритми арифметичних операцій над цілими невід’ємними числами у десятковій системі числення.
- Алгоритми переведення чисел з однієї позиційної системи числення в іншу
- Але відмінні від значення функції в точці або значення не існує, то точка називається точкою усувного розриву функції .
- Аналіз коефіцієнтів цільової функції
- Аналіз однієї ознаки
| <== попередня сторінка | | | наступна сторінка ==> |
| Елементи аналітичної геометрії. | | | Короткі теоретичні відомості |
|
Не знайшли потрібну інформацію? Скористайтесь пошуком google: |
© studopedia.com.ua При використанні або копіюванні матеріалів пряме посилання на сайт обов'язкове. |