
РЕЗОЛЮЦІЯ: Громадського обговорення навчальної програми статевого виховання
ЧОМУ ФОНД ОЛЕНИ ПІНЧУК І МОЗ УКРАЇНИ ПРОПАГУЮТЬ "СЕКСУАЛЬНІ УРОКИ"
ЕКЗИСТЕНЦІЙНО-ПСИХОЛОГІЧНІ ОСНОВИ ПОРУШЕННЯ СТАТЕВОЇ ІДЕНТИЧНОСТІ ПІДЛІТКІВ
Батьківський, громадянський рух в Україні закликає МОН зупинити тотальну сексуалізацію дітей і підлітків
Відкрите звернення Міністру освіти й науки України - Гриневич Лілії Михайлівні
Представництво українського жіноцтва в ООН: низький рівень культури спілкування в соціальних мережах
Гендерна антидискримінаційна експертиза може зробити нас моральними рабами
ЛІВИЙ МАРКСИЗМ У НОВИХ ПІДРУЧНИКАХ ДЛЯ ШКОЛЯРІВ
ВІДКРИТА ЗАЯВА на підтримку позиції Ганни Турчинової та права кожної людини на свободу думки, світогляду та вираження поглядів
- Гідрологія і Гідрометрія
- Господарське право
- Економіка будівництва
- Економіка природокористування
- Економічна теорія
- Земельне право
- Історія України
- Кримінально виконавче право
- Медична радіологія
- Методи аналізу
- Міжнародне приватне право
- Міжнародний маркетинг
- Основи екології
- Предмет Політологія
- Соціальне страхування
- Технічні засоби організації дорожнього руху
- Товарознавство продовольчих товарів
Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция
Елементи аналітичної геометрії.
Розглянемо декартову прямокутну систему координат на площині. Точки в цій системі визначаються двома координатами: 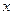 – абсциса та
– абсциса та 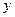 – ордината:
– ордината: 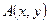 . Дві точки
. Дві точки  і
і  з’єднані прямою утворюють відрізок
з’єднані прямою утворюють відрізок  , довжина якого визначається формулою:
, довжина якого визначається формулою:  . Якщо точка
. Якщо точка 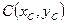 належить відрізку
належить відрізку  і ділить відрізок у відношенні
і ділить відрізок у відношенні 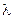 , а саме
, а саме  , то координати її визначаються формулами:
, то координати її визначаються формулами:  і
і 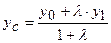 . Якщо
. Якщо 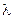 =1, то
=1, то 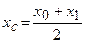 і
і 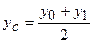 .
.
Пряма може бути задана рівняннями: а) з кутовим коефіцієнтом 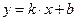 , де
, де 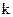 - кутовий коефіцієнт,
- кутовий коефіцієнт, 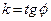 ,
, 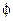 - кут, який пряма утворює з додатнім напрямком вісі
- кут, який пряма утворює з додатнім напрямком вісі  , а
, а  – відрізок, який пряма відтинає на вісі
– відрізок, який пряма відтинає на вісі  ; б) загальне рівняння прямої
; б) загальне рівняння прямої  ,
,  ; в) рівняння прямої, яка проходить через точку
; в) рівняння прямої, яка проходить через точку  , визначається
, визначається  ; г) якщо дві точки
; г) якщо дві точки  і
і  належать прямій, то рівняння її
належать прямій, то рівняння її  . Умова паралельності прямих
. Умова паралельності прямих 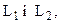 які мають відповідно кутові коефіцієнти
які мають відповідно кутові коефіцієнти  ,
, 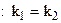 . Умова перпендикулярності цих прямих:
. Умова перпендикулярності цих прямих:  . Кут
. Кут 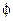 між цими прямими визначається формулою:
між цими прямими визначається формулою: 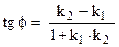 , де через
, де через 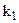 позначають коефіцієнт прямої, яку повертають проти руху стрілки годинника до збігу з другою прямою. Відстань від точки
позначають коефіцієнт прямої, яку повертають проти руху стрілки годинника до збігу з другою прямою. Відстань від точки 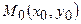 до прямої
до прямої  , заданої рівняння
, заданої рівняння  , визначається формулою:
, визначається формулою:  .
.
До ліній другого порядку належать наступні: а) коло з центром в точці  та радіусом
та радіусом  :
: 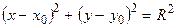 ; б) еліпс з центром в точці
; б) еліпс з центром в точці  та півосями
та півосями 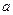 та
та  :
:  ; в) гіпербола з центром в точці
; в) гіпербола з центром в точці  , півосями
, півосями 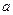 та
та  і асимптотами
і асимптотами  визначається формулою
визначається формулою 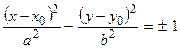 ; г) парабола з вершиною в точці
; г) парабола з вершиною в точці  визначається формулою:
визначається формулою:  або
або  , де
, де 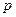 – параметр.
– параметр.
Рівняння лінії може бути задане в полярній системі координат:  , де
, де  - кут. Перехід від декартової системи координат до полярної системи координат здійснюється за формулами:
- кут. Перехід від декартової системи координат до полярної системи координат здійснюється за формулами:  і
і  . Перехід від полярної системи координат до декартової системи координат здійснюється за формулами:
. Перехід від полярної системи координат до декартової системи координат здійснюється за формулами: 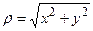 та
та  .
.
Розглянемо декартову прямокутну систему координат у просторі. Точки в цій системі визначаються трьома координатами: 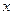 – абсциса,
– абсциса, 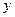 – ордината та
– ордината та 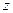 – апліката:
– апліката:  . Довжина відрізка у просторі та поділ відрізка в заданому відношенні визначається аналогічними формулами як для площини з урахуванням аплікати.
. Довжина відрізка у просторі та поділ відрізка в заданому відношенні визначається аналогічними формулами як для площини з урахуванням аплікати.
Площина у просторі характеризується нормальним вектором  , який перпендикулярний до площини. Площина у просторі задається рівняннями: а) рівняння площини, якій належить точка
, який перпендикулярний до площини. Площина у просторі задається рівняннями: а) рівняння площини, якій належить точка 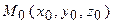 , визначається
, визначається
 ; б) загальне рівняння
; б) загальне рівняння 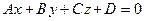 ; в) рівняння площини, якій належать точки
; в) рівняння площини, якій належать точки 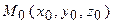 ,
, 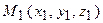 ,
,  , визначається формулою
, визначається формулою  ; г) рівняння площини у відрізках
; г) рівняння площини у відрізках 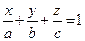 , де а,b,c – відрізки, які площина відтинає відповідно на осях
, де а,b,c – відрізки, які площина відтинає відповідно на осях  ,
,  ,
, 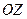 , враховуючи їх знаки; д) рівняння пучка площин
, враховуючи їх знаки; д) рівняння пучка площин
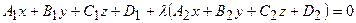 . Умова паралельності двох площин:
. Умова паралельності двох площин: 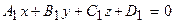 і
і  визначається:
визначається:  . Умова перпендикулярності цих площин:
. Умова перпендикулярності цих площин:  . Кут
. Кут 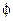 між цими площинами визначається формулою:
між цими площинами визначається формулою:
 .
.
Відстань від точки 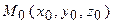 до площини
до площини 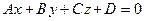 визначається формулою
визначається формулою
 .
.
Пряма у просторі характеризується напрямним вектором 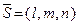 , який паралельний прямій. Пряма у просторі задається рівняннями: а) канонічні рівняння прямої:
, який паралельний прямій. Пряма у просторі задається рівняннями: а) канонічні рівняння прямої: 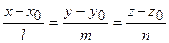 , де точка
, де точка 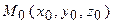 належить прямій; б) параметричні рівняння прямої:
належить прямій; б) параметричні рівняння прямої: 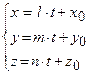 ; в) рівняння прямої, якій належать дві точки
; в) рівняння прямої, якій належать дві точки 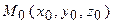 і
і 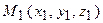 визначається формулою:
визначається формулою: 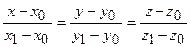 ; г) пряма, як перетин двох площин
; г) пряма, як перетин двох площин 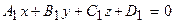 і
і  , визначається формулою:
, визначається формулою: 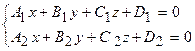 . Кут між двома прямими з напрямними векторами
. Кут між двома прямими з напрямними векторами 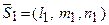 і
і 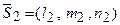 визначається формулою:
визначається формулою:  . Умова паралельності двох прямих:
. Умова паралельності двох прямих:  , умова перпендикулярності двох прямих:
, умова перпендикулярності двох прямих:  .
.
Кут між прямою 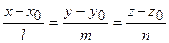 з напрямним вектором
з напрямним вектором 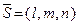 і площиною
і площиною  з нормальним вектором
з нормальним вектором  визначається формулою:
визначається формулою: 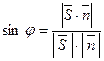 . Якщо пряма і площина перпендикулярні, то
. Якщо пряма і площина перпендикулярні, то  . Якщо пряма і площина паралельні, то
. Якщо пряма і площина паралельні, то 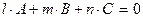 .
.
Задача 10. Дані вершини трикутника 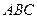 :
:  ,
, 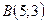 ,
,  . Знайти: а) Довжину та рівняння сторони
. Знайти: а) Довжину та рівняння сторони  , б) Довжину та рівняння висоти, проведеної з вершини
, б) Довжину та рівняння висоти, проведеної з вершини  , в) Рівняння прямої, проведеної через точку
, в) Рівняння прямої, проведеної через точку  паралельно стороні
паралельно стороні  , г) Рівняння середньої лінії, яка з'єднує сторони
, г) Рівняння середньої лінії, яка з'єднує сторони  і
і 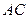 , д) Кут при вершині
, д) Кут при вершині 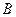 . Зробити рисунок.
. Зробити рисунок.
Розв’язання: Зробимо рисунок:


а) Рівняння  :
: 
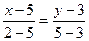
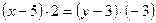 ;
; 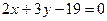 (
(  )
)
Довжина  :
:
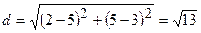
б) Висота 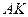 і сторона
і сторона  перпендикулярні, тому
перпендикулярні, тому 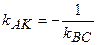 . З рівняння
. З рівняння  маємо
маємо 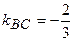 , тоді
, тоді 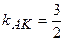 . Для прямої
. Для прямої 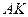 відомі координати точки
відомі координати точки  і кутовий коефіцієнт. Рівняння
і кутовий коефіцієнт. Рівняння 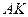 :
:
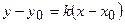



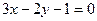
Довжина висоти – це відстань від точки  до прямої
до прямої  :
:

в) Пряма 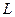 , що проходить через точку
, що проходить через точку  , паралельна стороні
, паралельна стороні  . Їх кутові коефіцієнти рівні:
. Їх кутові коефіцієнти рівні:  . Отримаємо її рівняння:
. Отримаємо її рівняння:



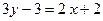
 (
( 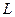 )
)
г) Середня лінія проходить через середини сторін  і
і 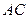 . Нехай це точки
. Нехай це точки  і
і  відповідно. Знайдемо їх координати:
відповідно. Знайдемо їх координати:

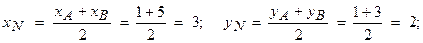
Рівняння середньої лінії 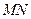 :
:



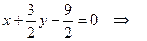

д) Щоб утворити кут 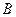 , треба пряму
, треба пряму  повернути проти стрілки годинника до збігу з прямою
повернути проти стрілки годинника до збігу з прямою  . Рівняння прямої
. Рівняння прямої 
 , тому
, тому 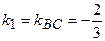 . Рівняння
. Рівняння  :
: 



 , тому
, тому  .
.
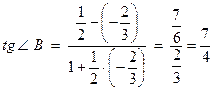 ,
, 
Задача 11.Рівняння кривих привести до канонічного виду та побудувати їх
а)  – рівняння гіперболи.
– рівняння гіперболи.
Розв’язання: Методом доповнення до повного квадрата виділяємо повний квадрат по змінних 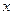 і
і 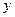 :
:
 ,
,
 ,
,
 ,
,
 ,
,
 .
.
Виконаємо паралельний перенос координат 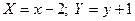 з новим центром в точці
з новим центром в точці  . Рівняння має вигляд:
. Рівняння має вигляд: 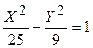
Рівняння асимптот в «новій» системі координат 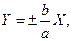 де
де
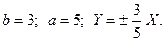 Зробимо рисунок:
Зробимо рисунок:

б) 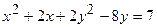 – рівняння еліпса.
– рівняння еліпса.
Розв’язання: Виділяємо повний квадрат по змінних 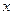 і
і 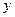 :
:
 ,
,
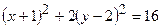 ,
,
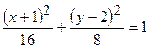 .
.
Виконаємо паралельний перенос координат 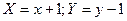 з новим центром в точці
з новим центром в точці  . Рівняння має вигляд:
. Рівняння має вигляд:  . Зробимо рисунок:
. Зробимо рисунок:
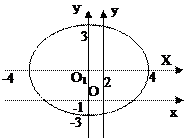 |
в)  – рівняння параболи.
– рівняння параболи.
Розв’язання: Виділяємо повний квадрат по змінній 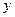 :
: 


Виконаємо паралельний перенос координат 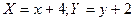 з новим центром в точці
з новим центром в точці  . Рівняння має вигляд:
. Рівняння має вигляд:  .
.
 Зробимо рисунок:
Зробимо рисунок:
 | |
 |
Задача 12. Скласти рівняння площини, яка проходить через точку 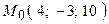 перпендикулярно до заданої прямої
перпендикулярно до заданої прямої 
Розв’язання: Напрямний вектор прямої 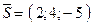 . Так як пряма і площина перпендикулярні, то
. Так як пряма і площина перпендикулярні, то  , де
, де  – нормальний вектор площини. Тоді
– нормальний вектор площини. Тоді  . Рівняння площини складаємо за формулою:
. Рівняння площини складаємо за формулою:  , де
, де  і
і 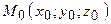 . Матимемо:
. Матимемо:  .
.
У підсумку матимемо  .
.
Задача 13. Дано чотири точки:  ,
, 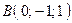 ,
,  і
і  . Знайти рівняння прямої, яка проходить через точку
. Знайти рівняння прямої, яка проходить через точку  перпендикулярно площині
перпендикулярно площині 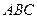 .
.
Розв’язання: Складемо рівняння площини 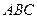 , яка проходить через три точки
, яка проходить через три точки  :
:
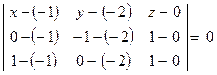

Розкриємо визначник по елементах першого рядка. Матимемо: 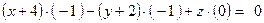 . Тоді вектор нормалі площини
. Тоді вектор нормалі площини 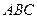
 або
або 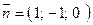 . З умови перпендикулярності прямої і площини:
. З умови перпендикулярності прямої і площини:  матимемо
матимемо 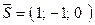 . Тому канонічні рівняння прямої
. Тому канонічні рівняння прямої
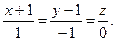
Задача 14.Скласти рівняння площини, яка проходить через точку  та пряму
та пряму 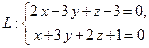 .
.
Розв’язання: Пряма  задана як перетин двох площин. Через цю пряму можна провести безліч площин, які ми називаємо пучком площин. Запишемо рівняння пучка для наших площин
задана як перетин двох площин. Через цю пряму можна провести безліч площин, які ми називаємо пучком площин. Запишемо рівняння пучка для наших площин
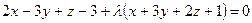
За умовою задачі площина проходить через точку  . Підставимо координати точки в рівняння і знайдемо
. Підставимо координати точки в рівняння і знайдемо 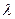 .
.
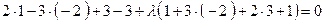
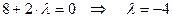
Знайдене значення 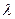 підставимо в рівняння пучка:
підставимо в рівняння пучка: 
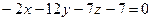 Рівняння площини:
Рівняння площини: 
Задача 15.Знайти кут між прямою  та площиною
та площиною  .
.
Розв’язання: Напрямний вектор прямої  нормальний вектор площини
нормальний вектор площини  . Кут між ними
. Кут між ними 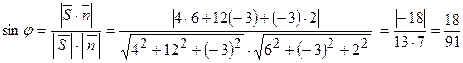 Тоді
Тоді  .
.
Читайте також:
- II. Елементи операційних витрат
- Аграрна структура та її елементи
- Адміністративне правопорушення як підстава юридичної відповідальності: ознаки і елементи
- Адміністративне правопорушення як підстава юридичної відповідальності: ознаки і елементи.
- Азот, фосфор, біогенні елементи та їх сполуки, органічні речовини
- АКУСТИКА. ЕЛЕМЕНТИ ФІЗИКИ СЛУХУ. ОСНОВИ АУДІОМЕТРІЇ
- Аналітична обробка інформації вузлами інформаційно-аналітичної функціональної підсистеми МОЗ України і питань НС.
- Базові елементи управління проектом
- Біоелементи.
- Будова й основні елементи машини
- Валідація НАССР- отримання об'єктивного доказу того, що елементи НАССР-плану результативні.
- Валютна система та її елементи
| <== попередня сторінка | | | наступна сторінка ==> |
| Елементи векторної алгебри. | | | Диференціальне числення функції однієї змінної. |
|
Не знайшли потрібну інформацію? Скористайтесь пошуком google: |
© studopedia.com.ua При використанні або копіюванні матеріалів пряме посилання на сайт обов'язкове. |