
РЕЗОЛЮЦІЯ: Громадського обговорення навчальної програми статевого виховання
ЧОМУ ФОНД ОЛЕНИ ПІНЧУК І МОЗ УКРАЇНИ ПРОПАГУЮТЬ "СЕКСУАЛЬНІ УРОКИ"
ЕКЗИСТЕНЦІЙНО-ПСИХОЛОГІЧНІ ОСНОВИ ПОРУШЕННЯ СТАТЕВОЇ ІДЕНТИЧНОСТІ ПІДЛІТКІВ
Батьківський, громадянський рух в Україні закликає МОН зупинити тотальну сексуалізацію дітей і підлітків
Відкрите звернення Міністру освіти й науки України - Гриневич Лілії Михайлівні
Представництво українського жіноцтва в ООН: низький рівень культури спілкування в соціальних мережах
Гендерна антидискримінаційна експертиза може зробити нас моральними рабами
ЛІВИЙ МАРКСИЗМ У НОВИХ ПІДРУЧНИКАХ ДЛЯ ШКОЛЯРІВ
ВІДКРИТА ЗАЯВА на підтримку позиції Ганни Турчинової та права кожної людини на свободу думки, світогляду та вираження поглядів
- Гідрологія і Гідрометрія
- Господарське право
- Економіка будівництва
- Економіка природокористування
- Економічна теорія
- Земельне право
- Історія України
- Кримінально виконавче право
- Медична радіологія
- Методи аналізу
- Міжнародне приватне право
- Міжнародний маркетинг
- Основи екології
- Предмет Політологія
- Соціальне страхування
- Технічні засоби організації дорожнього руху
- Товарознавство продовольчих товарів
Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция
Елементи векторної алгебри.
Координати вектора  визначаються формулою
визначаються формулою 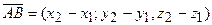 , якщо задані точки
, якщо задані точки 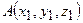 і
і 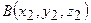 .
.
Вектори 
 і
і  можна додавати і віднімати
можна додавати і віднімати 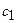
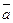
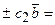
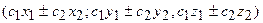 , де
, де 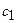 і
і 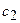 довільні сталі. Якщо вектори
довільні сталі. Якщо вектори 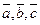 лінійно незалежні, то вони утворюють базис і вектор
лінійно незалежні, то вони утворюють базис і вектор 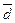 може бути розкладений по цьому базису:
може бути розкладений по цьому базису: 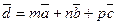 , де
, де 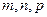 – деякі числа. Якщо вектори
– деякі числа. Якщо вектори 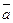 і
і 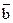 колінеарні, то їх координати пропорційні:
колінеарні, то їх координати пропорційні: 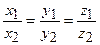 .
.
Скалярний добуток векторів 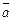 і
і 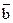 визначається (
визначається ( 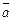
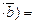
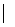
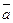
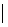
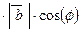 , де
, де 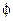 - кут між векторами
- кут між векторами 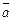 і
і 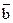 . Якщо вектори задані координатами, то скалярний добуток (
. Якщо вектори задані координатами, то скалярний добуток ( 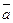
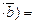

 . Умова перпендикулярності векторів: (
. Умова перпендикулярності векторів: ( 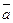
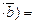 0. Довжина вектора:
0. Довжина вектора: 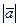
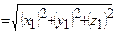 . Кут між векторами
. Кут між векторами 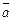 і
і 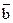 :
: 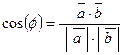 . Проекція вектора
. Проекція вектора 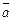 на вектор
на вектор 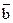 :
: 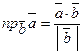 . Робота сили
. Робота сили 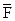 , яка прямолінійно переміщує матеріальну точку з початку в кінець вектора
, яка прямолінійно переміщує матеріальну точку з початку в кінець вектора  визначається формулою
визначається формулою  .
.
Векторним добутком векторів 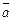 і
і 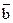 є вектор
є вектор  , що задовольняє умовам: а) вектор
, що задовольняє умовам: а) вектор  б) довжина вектора
б) довжина вектора  обчислюється за формулою:
обчислюється за формулою:  , де
, де 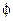 - кут між векторами
- кут між векторами 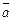 і
і 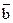 ; в)
; в)  утворюють праву трійку. Якщо вектори
утворюють праву трійку. Якщо вектори  задані координатами, то векторний добуток обчислюється як
задані координатами, то векторний добуток обчислюється як 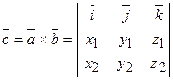 . Площа трикутника АВС, для якого задані координати вершин, обчислюється як
. Площа трикутника АВС, для якого задані координати вершин, обчислюється як 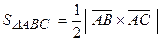 . Момент сили
. Момент сили 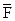 , прикладеної в точці
, прикладеної в точці  , відносно точки
, відносно точки 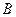 визначається векторним добутком
визначається векторним добутком 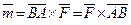 .
.
Мішаний добуток трьох векторів  - це векторно-скалярний добуток
- це векторно-скалярний добуток  , де
, де 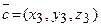 . Три вектори компланарні, якщо вони належать одній площині або паралельним площинам. Умова компланарності трьох векторів:
. Три вектори компланарні, якщо вони належать одній площині або паралельним площинам. Умова компланарності трьох векторів:  . Модуль мішаного добутку векторів
. Модуль мішаного добутку векторів  дорівнює об’єму паралелепіпеда, побудованого на цих векторах. Об’єм піраміди
дорівнює об’єму паралелепіпеда, побудованого на цих векторах. Об’єм піраміди 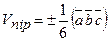 . Знак вибираємо таким чином, щоб об’єм був додатним.
. Знак вибираємо таким чином, щоб об’єм був додатним.
Задача 5.Перевірити колінеарність векторів 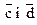 , побудованих на векторах
, побудованих на векторах 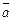 і
і 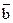 , якщо
, якщо 
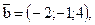

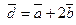 .
.
Розв’язання: Знайдемо координати векторів  :
:

 .
.
Перевіримо умову колінеарності векторів:

Вектори  не колінеарні, так як їх координати не пропорційні.
не колінеарні, так як їх координати не пропорційні.
Задача 6. Задані координати вершин піраміди  . Знайти:
. Знайти:
а) Кут між ребрами 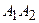 та
та  ; б) Площу грані
; б) Площу грані 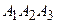 ; в) Проекцію вектора
; в) Проекцію вектора 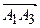 на вектор
на вектор 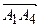 , г) Довжину висоти піраміди, проведену з вершини
, г) Довжину висоти піраміди, проведену з вершини 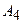 , д) Яку трійку утворюють вектори
, д) Яку трійку утворюють вектори  ,
, 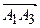 і
і 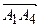 ?
?
Дано: 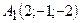 ,
, 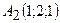 ,
, 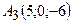 ,
, 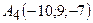 .
.
Розв’язання:
Знайдемо координати векторів, на яких побудована піраміда: 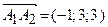 ,
,  ,
,  .
.
а) Тоді косинус кута між ребрами 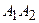 та
та  :
:

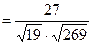 . Маємо
. Маємо 
б) Площу грані 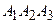 знайдемо, як половину модуля векторного добутку векторів
знайдемо, як половину модуля векторного добутку векторів  та
та 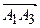 :
:
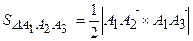 .
.

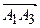 =
= 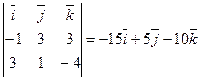
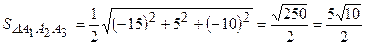 (кв.од.)
(кв.од.)
в) Проекцію 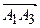 на
на 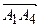 обчислюємо за формулою:
обчислюємо за формулою:
 г) Об’єм піраміди обчислимо, застосовуючи мішаний добуток векторів
г) Об’єм піраміди обчислимо, застосовуючи мішаний добуток векторів  ,
, 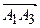 і
і 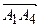 .
.
 ,
,  (куб.од.)
(куб.од.)
Для знаходження висоти піраміди застосовуємо формулу
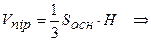
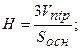
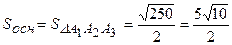 кв.од. і
кв.од. і 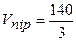 куб.од. Підставимо
куб.од. Підставимо  i
i  в формулу для обчислення висоти:
в формулу для обчислення висоти:
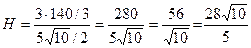 (лін.од.)
(лін.од.)
д)Так як мішаний добуток векторів 

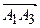

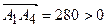 , то вони утворюють праву трійку.
, то вони утворюють праву трійку.
Задача 7.Визначити при якому значенні b вектори 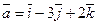 i
i  взаємно перпендикулярні.
взаємно перпендикулярні.
Розв’язання: Запишемо вектори в координатній формі: 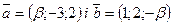 . Знайдемо скалярний добуток цих векторів:
. Знайдемо скалярний добуток цих векторів: 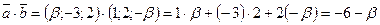 . З умови перпендикулярності векторів:
. З умови перпендикулярності векторів:  маємо
маємо
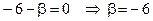 .
.
Задача 8.З’ясувати, чи належать чотири точки 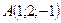 ,
, 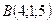 ,
, 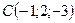 і
і 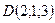 одній площині.
одній площині.
Розв’язання: Якщо 4 точки лежать в одній площині, то вектори 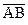 ,
, 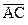 ,
, 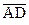 належать цій площині, отже будуть компланарні.
належать цій площині, отже будуть компланарні.
Перевіримо це. Знайдемо координати цих векторів: 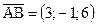
 ,
,  і їх мішаний добуток
і їх мішаний добуток

Вектори компланарні, точки А, В, С, D лежать в одній площині.
Задача 9. Дані сила 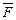 = (5;−1;2) і дві точки
= (5;−1;2) і дві точки 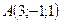 і
і  . Треба знайти: а) Роботу сили
. Треба знайти: а) Роботу сили  , необхідну для переміщення тіла із точки
, необхідну для переміщення тіла із точки  в точку
в точку 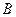 ; б) Момент сили
; б) Момент сили 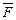 відносно точки
відносно точки  , якщо сила прикладена в точку
, якщо сила прикладена в точку 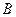 .
.
Розв’язання:
а) Робота А сили визначається як скалярний добуток сили 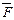 на вектор переміщення
на вектор переміщення  . Знайдемо координати вектора
. Знайдемо координати вектора  :
:
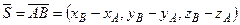
 = (0 − 3; 2 − (−1); −2 −1) = (− 3; 3;−3)
= (0 − 3; 2 − (−1); −2 −1) = (− 3; 3;−3)
Тоді 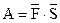 = ( 5; –1; 2 )×( –3; 3; –3) = 5
= ( 5; –1; 2 )×( –3; 3; –3) = 5  (–3) + (–1)×3 + 2
(–3) + (–1)×3 + 2  (–3) = = –15 –3 –6 = –24.
(–3) = = –15 –3 –6 = –24.
б) Момент 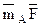 сили
сили 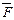 відносно точки
відносно точки 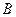 , якщо сила прикладена в точку
, якщо сила прикладена в точку  визначається як векторний добуток сили
визначається як векторний добуток сили 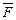 на плече
на плече  .
.
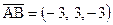 .
. 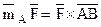
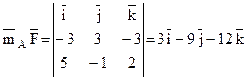
Читайте також:
- II. Елементи операційних витрат
- Аграрна структура та її елементи
- Адміністративне правопорушення як підстава юридичної відповідальності: ознаки і елементи
- Адміністративне правопорушення як підстава юридичної відповідальності: ознаки і елементи.
- Азот, фосфор, біогенні елементи та їх сполуки, органічні речовини
- АКУСТИКА. ЕЛЕМЕНТИ ФІЗИКИ СЛУХУ. ОСНОВИ АУДІОМЕТРІЇ
- Базові елементи управління проектом
- Біоелементи.
- Будова й основні елементи машини
- Валідація НАССР- отримання об'єктивного доказу того, що елементи НАССР-плану результативні.
- Валютна система та її елементи
- Вибір вогнегасної речовини та основні елементи устаткування водяного пожежогасіння
| <== попередня сторінка | | | наступна сторінка ==> |
| Вказівки до виконання контрольної роботи ( РГР ). | | | Елементи аналітичної геометрії. |
|
Не знайшли потрібну інформацію? Скористайтесь пошуком google: |
© studopedia.com.ua При використанні або копіюванні матеріалів пряме посилання на сайт обов'язкове. |