• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Вказівки до виконання контрольної роботи ( РГР ).

1.1.1 Елементи лінійної алгебри.

Числова матриця порядку 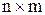– таблиця чисел, розташованих в рядках і стовпцях. Визначник n-го порядку – число , яке записується у вигляді

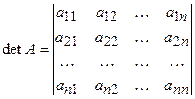Визначник обчислюється за

формулою: = 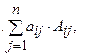i – фіксований індекс рядка.

Визначник 3-го порядку може обчислюватись за правилом трикутника або Саррюса. Дві матриці і 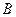множаться за формулою: 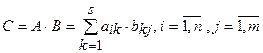. Обернена матриця 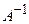для матриці існує, якщо . Вона обчислюється за формулою: 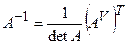, де 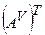– транспонована матриця 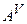. Матриця 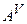складається з алгебраїчних доповнень до елементів матриці . Обернена матриця для матриці третього порядку має вигляд: ,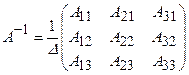

де 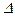= , 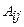–алгебраїчні доповнення до елементів матриці .

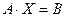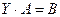Обернену матрицю застосовують при розв’язуванні матричного рівняння: або , де , , 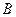, 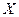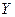– матриці, при цьому . Розв’язком цих рівнянь є 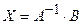або .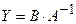

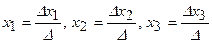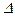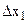
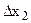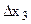Систему лінійних неоднорідних алгебраїчних рівнянь (СЛАР) можна розв’язувати за формулами Крамера, матричним методом, методом Гаусса та іншими. Розглянемо систему трьох лінійних рівнянь з трьома невідомими: Формули Крамера для неї: , де = – визначник системи, , – визначники невідомих.

Матричний метод розв’язання СЛАР полягає в наступному: система записується матричним рівнянням: 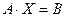, де – матриця системи, 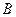– стовпець вільних членів, 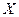– стовпець невідомих. Розв’язок системи знаходиться за формулою: .

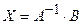Метод Гаусса полягає в послідовному виключенні невідомих, система приводиться до трикутного виду (прямий хід), а потім, починаючи з останнього рівняння системи, послідовно знаходяться невідомі. Систему записують у вигляді розширеної матриці (це матриця системи до якої приєднується стовпець вільних членів), яку за допомогою елементарних перетворень рядків приводять до трикутного виду. Отриману матрицю записують у вигляді системи, яку розв’язують, починаючи з останнього рівняння.

Якщо вільні члени СЛАР одночасно рівні нулю, то маємо однорідну СЛАР. Якщо 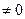, система має єдиний розв’язок – нульовий. У противному випадку – безліч розв’язків.

Наприклад, для системи трьох лінійних однорідних рівнянь з трьома невідомими, коли 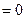, матимемо систему двох лінійних однорідних рівнянь з трьома невідомими:

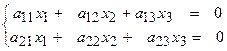, де 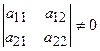. Розв’язок цієї системи дають формули: , , ,

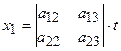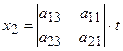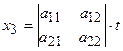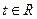
Теорема Кронекера-Капеллі дозволяє встановити сумісність системи лінійних неоднорідних алгебраїчних рівнянь.

Задача 1.Знайти обернену матрицю 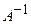до матриці . Результат перевірити, знайшовши добуток .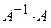

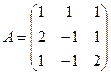
Розв’язання: а) обчислимо , розкладаючи його по першому рядку:

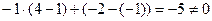. Обернена матриця існує.

б) знайдемо алгебраїчні доповнення 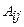кожного елемента матриці

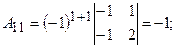
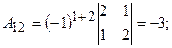
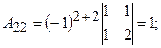
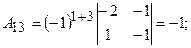
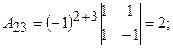
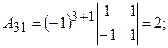
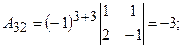
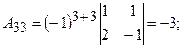
в) складемо матрицю із алгебраїчних доповнень:

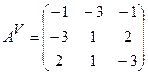
г) транспонуємо отриману матрицю:

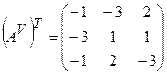
д) останню матрицю помножимо на 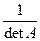, тобто на (-1/5) і отримаємо обернену матрицю.

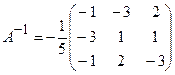
Перевірка.

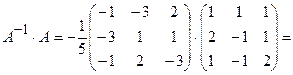
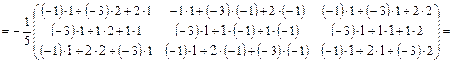
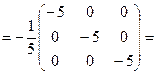
Задача 2. Розв’язати матричне рівняння:

.

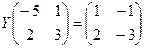Розв’язання: Маємо де

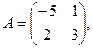
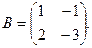
Знаходимо то 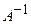існує і розв’язок рівняння буде 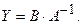Знайдемо 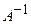. Алгебраїчні доповнення до елементів матриці : ; ;

;

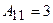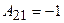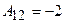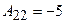
Запишемо обернену матрицю :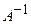

.

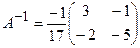
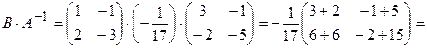
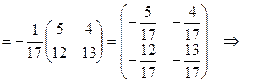
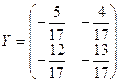Задача 3. Розв’язати неоднорідну систему лінійних алгебраїчних рівнянь трьома способами: а) за формулами Крамера, б) матричним методом, в) методом Гаусса.

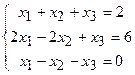
Розв’язання:

а) за формулами Крамера: Знайдемо визначники 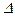, , 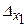, 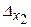. Обчислимо їх за правилом трикутників:

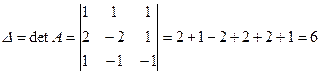
Послідовно замінюючи в D перший, другий і третій стовпець стовпцем вільних членів, знайдемо:

Δ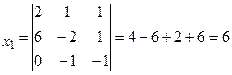

Δ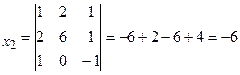

Δ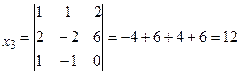

За формулами Крамера:

.

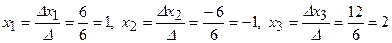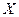б) матричним методом : Нехай – матриця системи, – матриця-стовпець невідомих, 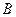– матриця-стовпець вільних членів:

.

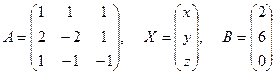Систему можна записати у вигляді: 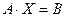і розв’язок системи 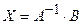. Матриця 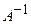є оберненою до матриці . Знайдемо її.

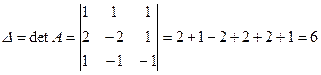
Знайдемо алгебраїчні доповнення:

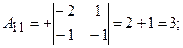
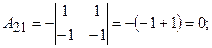
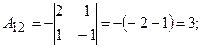
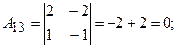
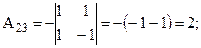
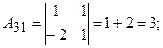
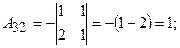
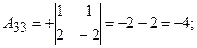
Обернена матриця:

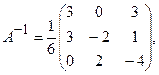
тоді:

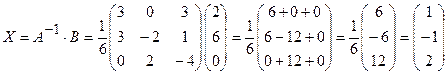
Розв^’язок системи: , , .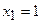

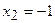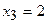в) методом Гаусса: Запишемо розширену матрицю 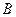системи, приєднавши до матриці системи стовпець вільних членів, і приведемо її до трикутного вигляду.

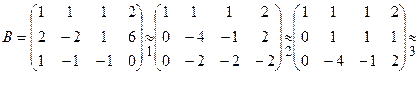
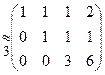. Знак » означає перехід від однієї матриці до другої, за допомогою елементарних перетворень. Таких переходів отримали 3, вони пронумеровані. Перший перехід: 1-й рядок залишаємо без змін, до 2-го додаємо 1-й, помножений на (-2), до 3-го додаємо 1-й, помножений на (-1). Другий перехід: скорочуємо 3-й рядок на (-2) і міняємо місцями 2-й і 3-й рядки. Третій перехід: 1-й і 2-й рядки залишаємо без зміни, до 3-го додаємо 2-й, помножений на 4. Мета перетворень – отримати матрицю трикутного виду. Останню матрицю записуємо у вигляді системи : .

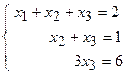З останнього рівняння отримаємо 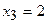, з другого 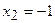, з першого .

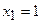Задача 4.Знайти розв^’язок систем лінійних однорідних рівнянь.

a)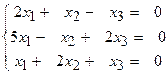

Розв’язання: Визначник системи 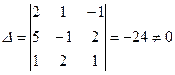, тому система має єдиний розв’язок : .

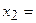
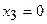б)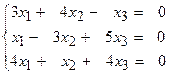

Розв’язання: Визначник системи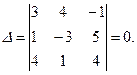

Отже система має безліч розв^’язків. Знайдемо загальний розв’язок системи. Третє рівняння є сумою перших двох рівнянь, тому його можна відкинути. Розглянемо систему двох рівнянь:

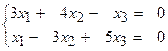
Застосуємо формули для знаходження розв’язку системи:

, , ,

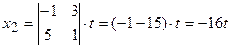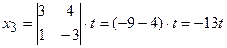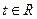
Читайте також:

1. I. Аналіз контрольної роботи.
2. I. ЗАГАЛЬНІ МЕТОДИЧНІ ВКАЗІВКИ
3. I. ОСНОВНІ ЕТАПИ ВИКОНАННЯ КУРСОВОЇ РОБОТИ
4. II. Вимоги безпеки перед початком роботи
5. II. Вимоги безпеки праці перед початком роботи
6. II. МЕТОДИЧНІ ВКАЗІВКИ
7. II. СТРУКТУРА ТА ОБСЯГ КУРСОВОЇ РОБОТИ
8. II.ТЕОРЕТИЧНІ ПИТАННЯ КУРСОВОЇ РОБОТИ
9. III ОФОРМЛЕННЯ І ЗАХИСТ РОБОТИ
10. III. Виконання бюджету
11. III. Вимоги безпеки під час виконання роботи
12. III. Вимоги безпеки під час виконання роботи

Переглядів: 714