• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция

Основні положення теми

Для того щоб кількісно описати зв’язок між кількома або багатьма змінними, одна з яких є залежною, інші — незалежними змінними, необхідно розглянути лінійну економетричну модель, яка базується на регресійному аналізі.

У загальному вигляді цю модель можна записати так:

де 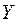— залежна змінна;

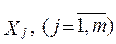— незалежні змінні;

u — стохастична складова.

Залежна змінна Y називається також пояснюваною, ендогенною змінною, незалежні змінні X_j — пояснюючими, предетермінованими, екзогенними змінними.

Аналітична форма загальної лінійної економетричної моделі:

,

де — параметри моделі.

В матричній формі економетрична модель має такий вигляд:

,

X — матриця незалежних змінних; A — вектор оцінок параметрів моделі; u — вектор залишків.

Щоб оцінити параметри моделі на основі методу 1МНК, необхідно дотримуватися таких передумов (гіпотез):

1) математичне сподівання залишків має дорівнювати нулю, тобто

;

2) значення вектора залишків u незалежні між собою і мають постійну дисперсію:

3) незалежні змінні моделі не зв’язані із залишками, тобто

;

4) незалежні змінні моделі створюють лінійно-незалежну систему векторів, тобто

Оператор оцінювання параметрів моделі на основі 1МНК:

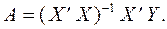
Неважко довести, що оцінки , які можна отримати на основі оператора оцінювання 1МНК, мінімізують суму квадратів залишків u. При цьому значення вектора є розв’язком нормальної системи рівнянь:

Якщо незалежні змінні в матриці X взяті як відхилення кожного значення від своєї середньої, то матрицю називають матрицею моментів. Числа, що стоять на її головній діагоналі, характеризують величину дисперсій незалежних змінних, інші елементи відповідають взаємним коваріаціям.

Оцінки параметрів загальної економетричної моделі повинні мати такі властивості:

1) незміщеності;

2) обгрунтованості;

3) ефективності;

4) інваріантності.

Оцінка параметра моделі буде незміщеною, коли дотримується рівність:

.

Якщо ця рівність не дотримується, то різниця 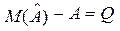називається зміщенням оцінки.

Оцінка параметра моделі буде обгрунтованою, якщо при заданій малій величині 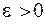справедливе відношення:

.

Оцінки параметрів A називаються ефективними, коли вони мають найменшу дисперсію.

Якщо функція 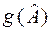відповідає функції , то оцінки параметрів A є інваріантними.

Читайте також:

1. I. Загальні положення
2. I. Загальні положення
3. I. ОСНОВНІ ЕТАПИ ВИКОНАННЯ КУРСОВОЇ РОБОТИ
4. II. ЗАГАЛЬНІ ПОЛОЖЕННЯ.
5. II. Основні закономірності ходу і розгалуження судин великого і малого кіл кровообігу
6. II. Основні засоби
7. II. ОСНОВНІ ПОВНОВАЖЕННЯ ТРУДОВИХ КОЛЕКТИВІВ
8. II.3. Основні способи і прийоми досягнення адекватності
9. III. Вправи з початкового положення стоячи.
10. III. Основні обов'язки робітників та службовців
11. IV. Основні обов'язки адміністрації
12. ORG - Встановити положення в сегменті

Переглядів: 429