Новини освіти і науки:

G+

Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция

Види і схеми відбору одиниць

Для того, щоб вибірка була репрезентативною, тобто давала правильне уявлення про генеральну сукупність, відбір одиниць з генеральної сукупності повинний бути відповідним чином організований.

Формування вибіркової сукупності з генеральної може здійснюватися по-різному:

– у залежності від виду і схеми відбору;

– зміни одиниці відбору і т.ін.

Від цих особливостей залежить розмір помилки вибірки і методи її визначення.

У залежності від того, як організований відбір одиниць з генеральної сукупності (загальної їхньої маси), розрізняють наступні види відбору:

– власне-випадковий (простий випадковий):

– механічний (систематичний);

– типовий (районований, розшарований, стратифікований, страт-район);

– серійний (гніздовий);

– комбінований.

За схемою відбору одиниць з генеральної сукупності вибірка може бути повторною і безповторною.

Власне-випадковий відбір – представляє таку організацію вибіркового спостереження, при якій відбір одиниць з генеральної сукупності здійснюється цілком випадково – навмання, за жеребом, чи, найчастіше, за допомогою таблиці випадкових чисел.

Він ще називається схемою «урн» чи «куль». При цьому забезпечується рівна імовірність кожній одиниці генеральної сукупності потрапити у вибірку.

НАПРИКЛАД, у відділі кадрів якогось підприємства є деяка кількість (сукупність) анкет усіх працівників. Наша задача установити вибірковим методом відсоток працівників, що мають повну середню освіту.

З загальної множини анкет беремо навмання одну, відзначаємо в себе на листі факт наявності чи відсутності середньої освіти в даного працівника і кладемо анкету назад. Потім беремо навмання іншу анкету, третю і т.д. У результаті такого відбору ми зберемо відомості про середню повну освіту у відношенні деякої вибіркової сукупності працюючих. Організоване таким способом вибіркове спостереження називається випадковою повторною вибіркою.

Випадкової вона називається тому, що при вилученні анкети (чи кулі з урни) ми не керувалися ніякими принципами, а вибирали навмання, як завгодно.

Повторної тому, що відібрану анкету (кулю) ми щораз кладемо назад у загальну Ії множину і, отже, існує імовірність того, що в одному з наступних вилучень вона може потрапити ще раз, повторно.

Т.ч., повторна вибірка – це вибірка, при якій існує імовірність повторного включення у вибіркову сукупність уже відібраної одиниці генеральної сукупності.

Повторна вибірка у практичній діяльності застосовується рідко, частіше застосовується безповторна, що дає більш точні результати.

При безповторнвй вибірці кожна відібрана одиниця не повертається у генеральну сукупність і в подальшому відборі вже не може взяти участь (схема кулі, що не повертається,).

Варто мати на увазі, що для того, щоб вибірка при власне-випадковому відборі була репрезентативною, необхідно, усе-таки, дотримуватися визначеного порядку відбору одиниць. Тобто його найкраще здійснювати за допомогою таблиці випадкових чисел, або таблиці логарифмів. Безладний же відбір може привести до систематичних помилок, що тягнуть за собою зміщення вибіркової середньої.

Власне-випадковий відбір є одним з перших, розроблених статистикою. Він дає гарні результати в тому випадку, коли між одиницями досліджуваної сукупності немає різких розходжень. Найчастіше застосовується тоді, коли відомий обсяг генеральної сукупності. Типовий приклад «лототрон» чи відбір лотерейних квитків.

Механічний відбір – широко застосовується у практиці вибіркового спостереження, його ще називають систематичний. Являє собою послідовний відбір одиниць через рівні проміжки (інтервали) у порядку їхнього розташування у генеральній сукупності.

Тобто відбирається, наприклад, із множини анкет кожна п'ята, десята і т.ін. у залежності від того яку частку (відсоток) одиниць необхідно відібрати. Так, при 25 % вибірці, з генеральної сукупності відбирається кожна 4-я одиниця. Тобто крок інтервалу визначається як частка від розподілу .

Початкову одиницю відбору визначають як випадкове число, найчастіше в середині 1-го інтервалу.

Механічний відбір завжди безповторний і більш ефективний чим простий випадковий. Особливо зручний у випадках коли чисельність генеральної сукупності невідома, чи відома приблизно.

Типовий відбір, його ще називають районованим, розшарованим чи стратифікованим. Суть його у тому, що генеральна сукупність розбивається на якісно однорідні, однотипні групи (райони) за типовою ознакою. Потім з кожної групи випадково відбирається певна кількість одиниць пропорційно питомій вазі групи у генеральній сукупності.

Так, наприклад, при відборі анкет працівників підприємства всю множину анкет спочатку розбивають на 3 групи: робітників, фахівців і керівників. Потім у межах кожної такої однорідної групи роблять відбір випадково чи механічно.

Типовий відбір може бути як повторним, так і безповторним у залежності від способу відбору в групах. Він більш доцільний у випадках, коли між одиницями генеральної сукупності є різкі розходження. Цей вид відбору дає більш точні результати, чим два попередніх, тому що:

– у вибірку в тій же пропорції, що й у генеральній сукупності, попадають представники всіх типових груп.

Вибірка при цьому стає більш репрезентативною і, отже, більш точною.

Серійний (гніздовий) відбір – при такому відборі відбираються не окремі одиниці сукупності, а групи одиниць, їх серії, гнізда власне-випадковим чи механічним способом. Потім у кожній із груп (серій) здійснюється суцільне спостереження.

НАПРИКЛАД: в університеті навчається 5 000 студентів у групах по 25 чоловік. Для проведення 10 %-го вибіркового спостереження серійним способом необхідно відібрати 500 студентів або ж 500:25 = 20 груп, тобто треба відібрати з 200 груп
[(5 000 : 25) = 200] 10 %, що і складе 20 груп. Далі у кожній з 20 груп проводиться суцільне спостереження.

Комбінований відбір – різновид, при якому поєднуються два чи кілька видів відбору одиниць з генеральної сукупності. Такий відбір ще називають східчастим, тому що він проходить кілька стадій – дві, три і більш. Кожна стадія має свою одиницю відбору, свою основу вибірки і свою частку відібраних одиниць.

НАПРИКЛАД, при обстеженні успішності студентів можна на першій стадії відібрати необхідну кількість груп, а потім, на 2-й –, число студентів з кожної групи. На 1-й стадії, у результаті, одиницею відбору буде група, на 2-й – студент. Вибірка на 1-й стадії може бути 15 %, а на другій – 5 %-а.

Багатофазна вибірка – характеризується тим, що на всіх її стадіях одиниця відбору залишається незмінною, але проводиться кілька стадій (фаз) вибіркового обстеження.

Обсяг вибірки на кожній фазі, як правило, різний. Особливістю багатофазної вибірки є те, що дані спостережень 1-й фази можна використовувати для додаткової характеристики 2-й фази і т.д. Тобто, дані кожної фази використовують як додаткову інформацію на наступній фазі, що дає більш точні результати. Багатофазна вибірка може бути поєднана також із суцільним статистичним спостереженням. При комбінованому відборі загальна помилка вибірки дорівнює сумі помилок кожної стадії.

Говорячи про різні види вибірки не можна не згадати про особливий спосіб – моментних спостережень, що почав застосовуватися у статистиці порівняно недавно.

При моментному спостереженні спостереженням охоплені всі елементи сукупності (як при суцільному спостереженні), але на певні моменти часу (вибіркове спостереження).

Тобто, об'єктом вибірки при моментному спостереженні є моменти чи відрізки часу. Тому поняття генеральної сукупності і вибіркової сукупності відносяться не до сукупності, що вивчається, а до часу спостереження.

НАПРИКЛАД, контрольні перевірки деканатом відвідування студентами занять охоплюють усіх студентів факультету, тому спостереження є суцільним. Але проводяться ці перевірки на певні моменти часу, тому за часом є вибірковими. Моментне спостереження дає можливість одержувати дані значно швидше і з меншими витратами, але з достатньою точністю.

Застосування моментного спостереження дає гарний результат при вивченні частки окремих елементів у якому-небудь процесі чи їх тривалості в якомусь процесі.

НАПРИКЛАД: необхідно визначити частку окремих витрат часу у загальному обсязі часу студентів. Для цього заздалегідь складається перелік можливого стану студента (відпочинок, обід, читання газет, перегляд телепередач, підготовка до занять, заняття і т.п.). Потім у визначені, заздалегідь обрані моменти часу відзначається в якому з перерахованих станів (з переліку) знаходиться студент у даний момент. Після декількох таких моментних спостережень на підставі зафіксованих оцінок визначається частка оцінок якого-небудь стану у загальній кількості оцінок.

Припустимо протягом 8-ми годин було зареєстровано 20 різних моментів. Серед них 10 – за елементом “заняття”, 2 – за елементом “відпочинок” і т.ін. Тоді час занять складе:

;

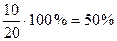час відпочинку: .

Вибір моментів спостереження може бути випадковим, або через певні інтервали часу (періодично).

Цей спосіб моментних спостережень отримав розповсюдження при вивченні структури витрат робочого часу, використання устаткування і т.п. Він менш трудомісткий ніж хронометраж чи фотографія робочого дня, а результати, при належній його організації, дає досить точні.

Читайте також:

<== попередня сторінка	\|	наступна сторінка ==>
Індекси змінного і фіксованого складу.	\|	Секторні і радіальні діаграми

Не знайшли потрібну інформацію? Скористайтесь пошуком google:

Генерація сторінки за: 0.004 сек.