• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Економіко-математичні методи, які застосовуються в економічному аналізі, їх класи­фікація

Зміст питання. Економіко-математичні методи, які застосовуються в економічному аналізі, їх класи­фікація. Лінійне й динамічне програмування, теорія масового обслуговування, сітьові графі­ки, транспортна задача та ін Особливості їх використання в аналізі господарської діяльності та сфери їхнього застосування

Застосування економіко-математичних методів (ЕММ) у системі функціонування організації викликано необхідністю підвищення ефективності процесів виробництва і обслуговування за умови раціонального використання наявних ресурсів через прийняття оптимальних управлінських рішень.

Основою формулювання економічної оптимізаційної задачі є можливість взаємозамінності способів виробництва товарів (надання послуг), допустимість багатьох варіантів використання матеріальних, трудових, фінансових, інформаційних ресурсів і вибору кращих з них.

Математичне програмування охоплює задачі пошуку екстремуму функції за наявності обмежень. Загальне завдання математичного програмування формулюється так: знайти величини керуючих факторів, при яких забезпечується максимум (мінімум) заданої цільової функції в області допустимих значень, що визначається деяким набором обмежень.

Оптимальність розв'язку означає, насамперед, його допустимість (тобто сумісність з усіма заданими умовами, що враховуються під час прийняття рішення). З усіх допустимих розв'язків оптимальним є той, для якого досягається екстремальне (максимальне чи мінімальне) значення критерію ефективної моделі. Формально багато проблем функціонування організацій можна пов'язати з раціональним використанням тих чи інших ресурсів, що дозволяє використати для їх розв'язання методи математичного програмування.

Загальна структура оптимізаційних моделей складається із цільової функції,яка набуває значення в межах обмеженого умовами задачі (області допустимих розв'язків), та із обмежень,що характеризують ці умови. Цільова функціяв загальному вигляді визначається трьома моментами: керованими змінними, некерованими параметрами (залежними, наприклад, від зовнішнього середовища) і видом (формою) залежності між ними (видом функції).

Загальний вигляд оптимізаційної моделі такий:

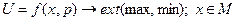
де U – критерій оптимальності;

х=(х_1, х_2,...,х_n) – керовані змінні;

р=(р_1, р_2,...,р_n) – параметри_;

М – задані межі (область) зміни керованих зміних.

Задачі такого виду розв'язують методами математичного програмування, в яке входить лінійне, нелінійне, динамічне, цілочислове програмування та ін. Вибір методів математичного програмування для розв'язування оптимізаційних задач визначається видом цільової функції: обмежень, що визначають область зміни керованих змінних (наприклад, вимоги їх чисельності). Розв'язок задачі називається оптимальним рішенням або оптимальним планом.

Задачі лінійного програмування. У загальному вигляді задача лінійного програмування (ЗЛП) формулюється так: знайти вектор х=(х_1, х_2,...,х_n) який максимізує (мінімізує) лінійну цільову функцію:

а також задовольняє лінійні функціональні обмеження:

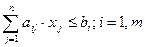
Крім того вектор повинен задовольняти прямі обмеження:

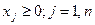
Ця задача може бути записаною в канонічній формі, при якій функціональні обмеження мають вигляд рівностей. Цього досягають додаванням до лівих частин цих обмежень m додаткових невід'ємних змінних. ЗЛП у канонічній формі розв'язують симплексним методом. Вирішення ЗЛП дає змогу знайти оптимальне управлінське рішення для різноманітних випадків, зокрема таких:

V оптимізація закріплення споживачів до постачальників;

V оптимізація завантаження виробничих потужностей;

V складання оптимальних сумішей (рецептів);

V оптимальний розкрій промислових матеріалів;

V оптимізація маршрутів комівояжерів тощо.

Задачі нелінійного програмування.Методи нелінійного програмування застосовують для розв'язування оптимізаційних задач, в яких цільова функція або обмеження (або перше і друге одночасно) характеризуються нелінійними залежностями. Ознаками нелінійності є, зокрема, наявність змінних, в яких показник степеня відмінний від одиниці, а також наявність змінного в показнику степеня, під коренем, під знаком логарифму. У разі нелінійності цільової функції оптимальне значення досягається не тільки на межі області допустимих значень (як це відбувається в задачах лінійного програмування), а всередині області, що значно ускладнює пошук оптимального значення. Також можливі варіанти, коли існуватимуть так звані локальні екстремальні точки, в той час як дослідника цікавить єдиний глобальний екстремум, де досягається шукане оптимальне значення. Нелінійність обмежень може привести до випадку з неопуклою областю допустимих значень, що надзвичайно ускладнює побудову ефективних алгоритмів пошуку оптимальних значень. З цього класу найбільш досліджені задачі з опуклими цільовими функціями при лінійного виду обмеженнях (існує єдиний оптимальний розв'язок). До розв'язування даного класу задач можна залучити ряд стандартних градієнтних або ньютонівських методів розв'язування. Ці методи реалізовані у спеціалізованих пакетах математичного програмного забезпечення.

Прикладомцього класу задач є задача про розміщення складів, коли необхідно мінімізувати загальну суму транспортних і складських витрат при таких обмеженнях:

=> з кожного підприємства повинна бути відвантаженою вся продукція;

=> не може бути перевищеною місткість будь-якого складу;

=> повинні бути задоволені всі замовлення усіх споживачів.

У процесі розв'язування задачі знаходять оптимальну за мінімумом затрат тричленну комбінацію: підприємство - склад - споживач.

Читайте також:

1. В незалежному економічному контролі
2. Використання статистичних методів в економічному аналізі.
3. Вимірника, які застосовуються в обліку
4. Вимірники, що застосовуються в обліку.
5. Власність як економічна категорія втілена в реальне економічне життя. Інтеграція виробництва — форма існування в реальному економічному житті усуспільнення виробництва.
6. Дискректна фіскальна політика:особливості, методи, проблеми
7. До фізико-хімічних методів очищення стічних вод нале­жать: коагуляція, сорбція (абсорбція, адсорбція), мембранні методи, іонний, обмінні, електроліз, екстракція.
8. Економіко-математичні методи аналізу
9. Економіко-математичні методи аналізу.
10. Економіко-математичні методи та моделі в економічному аналізі
11. Експортна діяльність у макро- та мікроекономічному вимірах

Переглядів: 1449