• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Ймовірність появи хоча б однієї події

Нехай у результаті випробування можуть з’явитися n подій, незалежних у сукупності, або деякі з них (зокрема, тільки одна чи ні одної), причому ймовірності появи кожної із подій відомі. Як знайти ймовірність того, що наступить хоча б одна з цих подій? Наприклад, якщо в результаті випробування можуть з’явитися три події, то поява хоча б одної з цих подій означає настання або одної, або двох, або трьох подій. Відповідь на поставлене питання дає наступна теорема.

Теорема.Ймовірність появи хоча б одної з подій 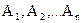, незалежних в сукупності, дорівнює різниці між одиницею і добутком ймовірностей протилежних подій :

.

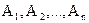Доведення. Позначимо через 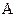подію, яка полягає в появі хоча б одної з подій 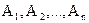. Поді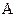ї і 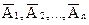(ні одна з подій не наступила) протилежні, значить сума їх ймовірностей дорівнює одиниці:

.

Звідси, користуючись теоремою множення, отримаємо

,

або

.

Частковий випадок. Якщо події 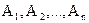мають однакову ймовірність, рівну 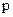, то ймовірність появи хоча б одної з цих подій

.

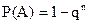Приклад 1. Ймовірності влучення в ціль при стрільбі з трьох гармат такі: p₁=0,8; p₂=0,7; р₃=0,9. Знайти ймовірність хоча б одного влучення (подія А) при одному залпі з усіх гармат.

Розв’язок. Ймовірність влучення в ціль кожною з гармат не залежить від результатів стрільби з інших гармат; тому розглянуті події А₁ (влучення першої гармати), A₂ (влучення другої гармати) і A₃ (влучення третьої гармати) незалежні в сукупності.

Ймовірності подій, протилежних подіям А₁ A₂ і A₃ (тобто ймовірності промахів), відповідно рівні:

;

;

.

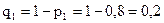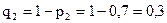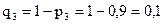Шукана ймовірність

.

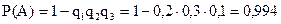Читайте також:

1. V. НАЙБІЛЬШ ВАЖЛИВІ ПОДІЇ І ДАТИ
2. А. Це наявність в однієї людини кількох ліній клітин з різним набором хромосом.
3. Алгоритми переведення чисел з однієї позиційної системи числення в іншу
4. Аналіз однієї ознаки
5. Безумовною є інформація про події, що реально відбуваються у матеріальному світі.
6. Визначте причини появи українського козацтва.
7. Визначте причини появи українського козацтва.
8. Виклик однієї форми з іншої
9. Виявлення, фіксація, вилучення речових доказів із місця події.
10. Відповідно до ст. 69 ЦПК перебіг процесуального строку починається з наступного дня після відповідної календарної дати або настання події, з якою пов'язано його початок.
11. Воєнно-політичні події 1649 – 1653 рр. Утворення Української гетьманської держави.
12. Вплив лютневої революції в Росії на події в Україні.

Переглядів: 7664