
РЕЗОЛЮЦІЯ: Громадського обговорення навчальної програми статевого виховання
ЧОМУ ФОНД ОЛЕНИ ПІНЧУК І МОЗ УКРАЇНИ ПРОПАГУЮТЬ "СЕКСУАЛЬНІ УРОКИ"
ЕКЗИСТЕНЦІЙНО-ПСИХОЛОГІЧНІ ОСНОВИ ПОРУШЕННЯ СТАТЕВОЇ ІДЕНТИЧНОСТІ ПІДЛІТКІВ
Батьківський, громадянський рух в Україні закликає МОН зупинити тотальну сексуалізацію дітей і підлітків
Відкрите звернення Міністру освіти й науки України - Гриневич Лілії Михайлівні
Представництво українського жіноцтва в ООН: низький рівень культури спілкування в соціальних мережах
Гендерна антидискримінаційна експертиза може зробити нас моральними рабами
ЛІВИЙ МАРКСИЗМ У НОВИХ ПІДРУЧНИКАХ ДЛЯ ШКОЛЯРІВ
ВІДКРИТА ЗАЯВА на підтримку позиції Ганни Турчинової та права кожної людини на свободу думки, світогляду та вираження поглядів
- Гідрологія і Гідрометрія
- Господарське право
- Економіка будівництва
- Економіка природокористування
- Економічна теорія
- Земельне право
- Історія України
- Кримінально виконавче право
- Медична радіологія
- Методи аналізу
- Міжнародне приватне право
- Міжнародний маркетинг
- Основи екології
- Предмет Політологія
- Соціальне страхування
- Технічні засоби організації дорожнього руху
- Товарознавство продовольчих товарів
Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция
Парабола
Канонічне рівняння гіперболи. Гіперболою називається множина точок площини, модуль різниці відстаней від кожної з яких до двох даних точок цієї площини є сталою величиною, меншою від відстані між даними точками. Дані точки називаються фокусами.
Позначимо фокуси через  ,
, 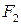 , відстань між ними
, відстань між ними 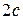 , а модуль різниці відстаней від будь-якої точки гіперболи до його фокусів – через
, а модуль різниці відстаней від будь-якої точки гіперболи до його фокусів – через  . Згідно означенню гіперболи
. Згідно означенню гіперболи 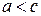 .
.
Для виведення рівняння гіперболи виберемо систему координат 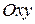 так, щоб фокуси
так, щоб фокуси  ,
, 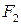 лежали на осі
лежали на осі 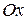 , а початок координат співпадав з серединою відрізка
, а початок координат співпадав з серединою відрізка 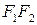 (рис. 9.4). Тоді фокуси матимуть координати
(рис. 9.4). Тоді фокуси матимуть координати  ,
,  .
.

Нехай  – довільна точка гіперболи. За означенням для довільної точки гіперболи і тільки для точок гіперболи справедлива рівність:
– довільна точка гіперболи. За означенням для довільної точки гіперболи і тільки для точок гіперболи справедлива рівність:
 або
або 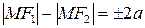 ,
,
тобто

– це і є рівняння гіперболи. Приведемо отримане рівняння до більш простого вигляду, як це було зроблено для еліпса. Отримаємо:
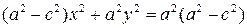 .
.
Так як 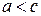 , то
, то 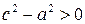 . Ввівши позначення
. Ввівши позначення  , отримаємо:
, отримаємо: 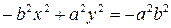 або
або
 (9.4)
(9.4)
Можна довести, що рівняння (9.4) рівносильне початковому рівнянню. Воно називається канонічним рівнянням гіперболи.
Дослідження форми гіперболи за її рівнянням.Координати  і
і  входять в рівняння (9.4) в парних степенях, тому гіпербола симетрична відносно осей координат і відносно початку координат.
входять в рівняння (9.4) в парних степенях, тому гіпербола симетрична відносно осей координат і відносно початку координат.
Для точок, що лежать в першій координатній чверті (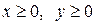 ) маємо
) маємо
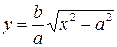 .
.
З цієї рівності випливає, що 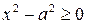
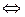
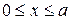 . При
. При  :
: 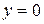 . При зростанні
. При зростанні  значення
значення  теж зростають, і точка
теж зростають, і точка  кривої при цьому необмежено віддаляється від осей
кривої при цьому необмежено віддаляється від осей 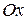 і
і  .
.
Побудуємо гіперболу в першій координатній чверті і, враховуючи симетрію, відобразимо побудовану частину відносно осей координат (рис. 9.5). Гіпербола складається з двох частин, які називаються вітками.
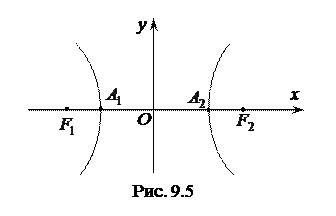
Центр симетрії  називають центром гіперболи. Точки
називають центром гіперболи. Точки 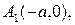
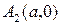 – точки перетину гіперболи з віссю
– точки перетину гіперболи з віссю 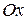 називають вершинами гіперболи. З віссю
називають вершинами гіперболи. З віссю  гіпербола не перетинається. Відрізок
гіпербола не перетинається. Відрізок 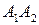 , а також його довжина
, а також його довжина  називаються дійсною віссю гіперболи, а число
називаються дійсною віссю гіперболи, а число 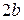 – уявною віссю гіперболи.
– уявною віссю гіперболи.
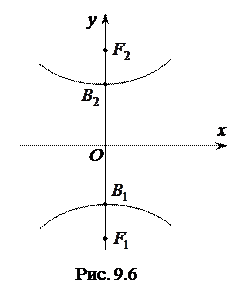
Рівняння  теж є рівнянням гіперболи. Фокуси такої гіперболи лежать на осі
теж є рівнянням гіперболи. Фокуси такої гіперболи лежать на осі  (рис. 9.6). В цьому випадку точки
(рис. 9.6). В цьому випадку точки 
 є вершинами гіперболи, а
є вершинами гіперболи, а 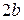 – дійсною віссю,
– дійсною віссю,  – уявною.
– уявною.
Якщо  , то гіпербола називається рівносторонньою.
, то гіпербола називається рівносторонньою.
Асимптоти гіперболи.Пряма  називається асимптотою необмеженої кривої
називається асимптотою необмеженої кривої 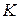 , якщо відстань
, якщо відстань  від точки
від точки  кривої
кривої 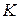 до цієї прямої прямує до нуля при необмеженому віддаленні точки
до цієї прямої прямує до нуля при необмеженому віддаленні точки  вздовж кривої
вздовж кривої 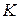 від початку координат (рис. 9.7).
від початку координат (рис. 9.7).

Покажемо, що гіпербола, задана рівнянням (9.4), має дві асимптоти:
 і
і  . (9.5)
. (9.5)
Так як прямі (9.5) і гіпербола (9.4) симетричні відносно осей координат, то достатньо розглянути тільки ті їх точки, що лежать в першій координатній чверті.
Візьмемо на прямій  точку
точку 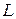 з такою ж абсцисою
з такою ж абсцисою  , як і в точки
, як і в точки  , що лежить на гіперболі
, що лежить на гіперболі 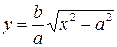 (рис. 9.8) і знайдемо різницю
(рис. 9.8) і знайдемо різницю  між ординатами прямої і вітки гіперболи:
між ординатами прямої і вітки гіперболи:

 .
.
Чисельник отриманого дробу є постійною величиною, а знаменник збільшується при зростанні  . Отже, довжина відрізка
. Отже, довжина відрізка 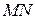 прямує до нуля при
прямує до нуля при  . Так як
. Так як  , то
, то 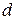 теж прямує до нуля. Таким чином, прямі
теж прямує до нуля. Таким чином, прямі
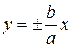
є асимптотами гіперболи.
Для гіперболи, заданої рівнянням  , асимптоти також мають вигляд (9.5).
, асимптоти також мають вигляд (9.5).
При побудові гіперболи доцільно спочатку побудувати прямокутник з центром симетрії в початку координат із сторонами  ,
, 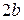 . Прямі, що проходять через протилежні вершини цього прямокутника, будуть асимптотами гіперболи.
. Прямі, що проходять через протилежні вершини цього прямокутника, будуть асимптотами гіперболи.
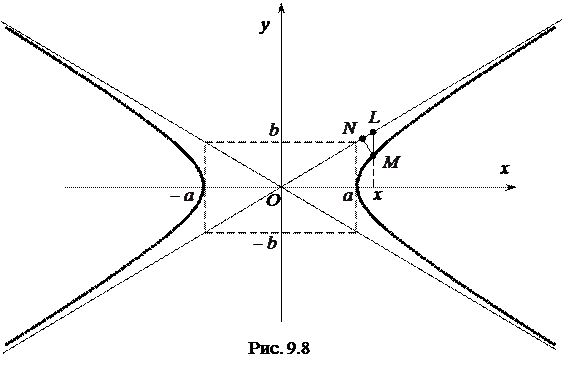
Ексцентриситет гіперболи. Відношення 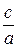 відстані між фокусами до довжини дійсної осі називають ексцентриситетомгіперболи і позначають
відстані між фокусами до довжини дійсної осі називають ексцентриситетомгіперболи і позначають  :
:
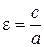 . (9.6)
. (9.6)
Так як 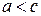 , то
, то  .
.
Ексцентриситет характеризує форму гіперболи. Дійсно, підставивши в формулу (9.6) 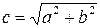 , отримаємо
, отримаємо
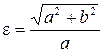 або
або 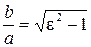 .
.
Звідси видно, що чим менше  , тим менше відношення
, тим менше відношення  і тим менші кути між асимптотами, в яких розташована гіпербола.
і тим менші кути між асимптотами, в яких розташована гіпербола.
Якщо гіпербола задана рівнянням  , то ексцентриситет знаходимо за формулою
, то ексцентриситет знаходимо за формулою  .
.
Приклад 9.3.Скласти канонічне рівняння гіперболи, фокуси якої лежать на осі 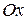 , якщо відстань між фокусами рівна 30, а дійсна вісь рівна 16.
, якщо відстань між фокусами рівна 30, а дійсна вісь рівна 16.
Розв’язок. Щоб скласти рівняння гіперболи, треба знайти 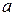 і
і 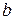 . За умовою
. За умовою  або
або 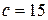 і
і 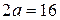 або
або 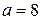 . Із співвідношення
. Із співвідношення 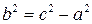 , отримаємо
, отримаємо  . Таким чином, шукане рівняння матиме вигляд
. Таким чином, шукане рівняння матиме вигляд
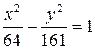 . t
. t
Приклад 9.4.Скласти канонічне рівняння гіперболи, фокуси якої лежать на осі  , якщо уявна вісь рівна 10, а ексцентриситет рівний
, якщо уявна вісь рівна 10, а ексцентриситет рівний  . Знайти її асимптоти.
. Знайти її асимптоти.
Розв’язок. Так як за умовою 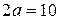 і
і  , то
, то  і
і 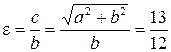 . Отримаємо:
. Отримаємо:  . Звідки
. Звідки  або
або 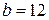 .
.
Отже, шукане рівняння гіперболи матиме вигляд
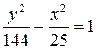 ,
,
а рівняння асимптот –
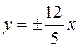 . t
. t
Читайте також:
| <== попередня сторінка | | | наступна сторінка ==> |
| Гіпербола | | | Еліпс, гіпербола, парабола з осями, паралельними осям координат |
|
Не знайшли потрібну інформацію? Скористайтесь пошуком google: |
© studopedia.com.ua При використанні або копіюванні матеріалів пряме посилання на сайт обов'язкове. |