• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Еліпс, гіпербола, парабола з осями, паралельними осям координат

Канонічне рівняння параболи. Параболою називається множина точок площини, кожна з яких однаково віддалена від даної точки і даної прямої. Дану точку називають фокусом, а дану пряму директрисою.

Позначимо фокус через . Відстань від фокуса до директриси називається параметром параболи і позначається .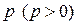

Для виведення рівняння параболи виберемо систему координат 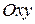так, щоб вісь 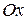проходила через фокус перпендикулярно директрисі в напрямку від директриси до фокуса. За початок координат виберемо середину між фокусом і точкою перетину директриси з віссю 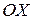. Тоді рівняння директриси матиме вигляд: , а координати фокуса (рис. 9.9).

Нехай – довільна точка параболи. Проведемо відрізок 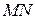перпендикулярно директрисі, тоді 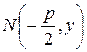За означенням для довільної точки параболи і тільки для точок параболи справедлива рівність:

, тобто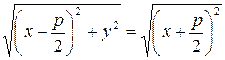

– це і є рівняння параболи. Приведемо отримане рівняння до більш простого вигляду. Для цього піднесемо обидві частини рівняння до квадрату і приведемо подібні, отримаємо:

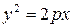. (9.7)

Можна довести, що рівняння (9.7) рівносильне початковому рівнянню. Воно називається канонічним рівнянням параболи.

Дослідження форми параболи за її рівнянням.Координата входить в рівняння (9.7) в парному степені, тому парабола симетрична відносно осі .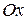

Так як 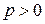, то з рівняння (9.7) випливає, що . А отже, парабола розташована справа від осі .

При : 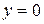– парабола проходить через початок координат і точка називається вершиною параболи.

При зростанні значення модуля теж зростають.

Парабола 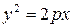побудована на рис. 9.10.

Рівняння , , теж є рівняннями параболи.

Парабола має нескінченні вітки. Асимптот у параболи немає.

Ексцентриситет параболи вважають рівним одиниці.

Приклад 9.5.Скласти канонічне рівняння параболи, якщо вона симетрична відносно осі 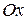і проходить через точку .

Розв’язок. Так як парабола симетрична відносно осі 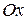, то її рівняння має вигляд . Підставимо координати точки в це рівняння, отримаємо: або , звідки 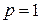. Отже, – шукане рівняння. t

Розглянемо еліпс з центром в точці з осями, паралельними осям координат (рис. 9.11).

Перейдемо від системи координат 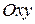до нової системи координат за допомогою паралельного переносу. При цьому початок координат перейде в точку , а осі 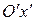, будуть паралельними осям 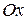, і однаково з ними направленими. Як відомо, формули перетворення координат при паралельному переносі осей координат на площині мають вигляд:

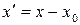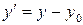, . (9.8)

Так як нові осі координат співпадають з осями еліпса, а початок координат – з його центром, то відносно системи координат канонічне рівняння еліпса матиме вигляд:

. (9.9)

Підставивши в рівняння (9.9) замість їх вирази з (9.8), отримаємо рівняння еліпса з центром в точці з осями, паралельними осям координат:

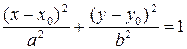. (9.10)

Аналогічно отримаємо рівняння гіперболи з центром в точці з осями, паралельними осям координат:

, (9.11)

якщо дійсна вісь паралельна осі 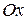, і

, (9.12)

якщо дійсна вісь паралельна осі .

Парабола з вершиною в точці задається рівнянням:

, (9.13)

якщо вісь симетрії паралельна ос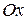і , і

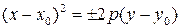, (9.14)

якщо вісь симетрії паралельна осі .

Рівняння (9.10) – (9.14) є рівняннями вигляду

.

Останнє є частинним випадком загального рівняння кривої другого порядку на площині

.

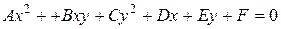Теоретичні питання

9.1. Що називається еліпсом?

9.2. Записати канонічне рівняння еліпса.

9.3. Що називається ексцентриситетом еліпса?

9.4. Що називається гіперболою?

9.5. Записати канонічне рівняння гіперболи.

9.6. Що називається асимптотою кривої?

9.7. Записати рівняння асимптот гіперболи.

9.8. Що називається ексцентриситетом гіперболи?

9.9. Що називається параболою?

9.10. Записати канонічне рівняння параболи.

9.11. Записати рівняння еліпса з центром в точці з осями, паралельними осям координат.

9.12. Записати рівняння гіперболи з центром в точці з осями, паралельними осям координат.

9.13. Записати рівняння параболи з вершиною в точці з осями, паралельними осям координат.

Задачі та вправи

9.1. Знайти довжини осей, координати фокусів і ексцентриситет еліпса .

9.2. Скласти канонічне рівняння еліпса, якщо:

а) ; б) ; в) ;

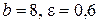г) ; д) ; е) .

9.3. Знайти рівняння гіперболи, що проходить через точки

і .

9.4. Знайти рівняння асимптот гіперболи 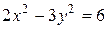та кут між ними.

9.5. Задана рівностороння гіпербола 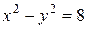. Знайти рівняння еліпса, фокуси якого співпадають з фокусами гіперболи, якщо відомо, що еліпс проходить через точку .

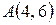9.6. Скласти рівняння параболи з вершиною в початку координат, симетричною відносно осі 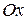, якщо відстань від її фокуса до вершини дорівнює 4.

9.7. Скласти рівняння параболи з вершиною в початку координат, симетричною відносно осі 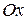, що проходить через точку .

Читайте також:

1. Вантажообіг і координати магазинів, які обслуговуються
2. Визначення скалярного добутку через координати.
3. Вираження мішаного добутку через координати векторів.
4. Декартова прямокутна система координат
5. Довжина дуги в прямокутних координатах.
6. Друга екваторіальна система координат
7. Замовник (підприємство, організація) надає ділянку (територію), обмежену координатами
8. Координатами.
9. КООРДИНАТОРИ ECTS
10. Координатори ECTS
11. Користувальницька система координат

Переглядів: 5392