Декартова прямокутна система координат

Нехай в просторі дано точку О і ортонормований базис, який позначатимемо .

Сукупність точки О і ортонормованого базису називається декартовою прямокутною системою координат в просторі. Точку О називають початком координат. Вісь, що проходить через точку О і має напрямок вектора 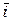, називається віссю 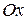або віссю абсцис; вісь, що проходить через точку О і має напрямок вектора 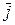– віссю або віссю ординат; вісь, що проходить через точку О і має напрямок вектора 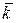– віссю 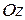або віссю аплікат. Осі 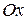, , 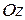називають осями координат. Площини, що проходять через дві осі координат, називають координатними площинами.

Декартову прямокутну систему координат позначають або .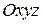

Радіус-вектором точки М назвемо вектор 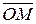(рис. 5.7). Нехай , де 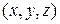– координати вектора 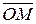в базисі , тобто його проекції на відповідні координатні осі, їх називають координатами точки Мв системі і записують . Координата називається абсцисою, – ординатою, – аплікатою.

Таким чином, кожній точці М в заданій декартовій прямокутній системі координат в просторі відповідає єдина впорядкована трійка чисел, і навпаки, кожній впорядкованій трійці чисел в заданій декартовій прямокутній системі координат в просторі відповідає єдина точка.

Знайдемо координати вектора , якщо відомі координати точок 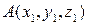, 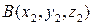. Маємо (рис. 5.8):

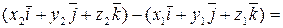
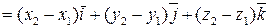Отже, координати вектора рівні різницям відповідних координат його кінця і початку.

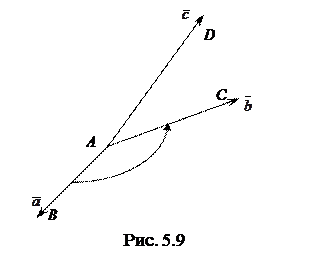Три некомпланарних вектори

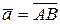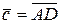, взятих у вказаному порядку, утворюють праву орієнтацію або праву трійку, якщо з кінця

поворот від

до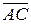

по найкоротшому шляху видно проти ходу стрілки годинника (рис. 5.9). В протилежному випадку трійка векторів утворює ліву трійку.

Якщо вектори утворюють праву (ліву) трійку, то, помінявши місцями довільні два вектори, отримаємо ліву (праву ) трійку.

Система координат називається правою, якщо її базисні вектори утворюють праву трійку і лівою, якщо – ліву.

Аналогічно визначається декартова прямокутна система координат на площині.

Читайте також:

<== попередня сторінка	\|	наступна сторінка ==>
Лінійні операції над векторами в координатній формі	\|	Поділ відрізка в даному відношенні

Не знайшли потрібну інформацію? Скористайтесь пошуком google:

Генерація сторінки за: 0.004 сек.