
РЕЗОЛЮЦІЯ: Громадського обговорення навчальної програми статевого виховання
ЧОМУ ФОНД ОЛЕНИ ПІНЧУК І МОЗ УКРАЇНИ ПРОПАГУЮТЬ "СЕКСУАЛЬНІ УРОКИ"
ЕКЗИСТЕНЦІЙНО-ПСИХОЛОГІЧНІ ОСНОВИ ПОРУШЕННЯ СТАТЕВОЇ ІДЕНТИЧНОСТІ ПІДЛІТКІВ
Батьківський, громадянський рух в Україні закликає МОН зупинити тотальну сексуалізацію дітей і підлітків
Відкрите звернення Міністру освіти й науки України - Гриневич Лілії Михайлівні
Представництво українського жіноцтва в ООН: низький рівень культури спілкування в соціальних мережах
Гендерна антидискримінаційна експертиза може зробити нас моральними рабами
ЛІВИЙ МАРКСИЗМ У НОВИХ ПІДРУЧНИКАХ ДЛЯ ШКОЛЯРІВ
ВІДКРИТА ЗАЯВА на підтримку позиції Ганни Турчинової та права кожної людини на свободу думки, світогляду та вираження поглядів
- Гідрологія і Гідрометрія
- Господарське право
- Економіка будівництва
- Економіка природокористування
- Економічна теорія
- Земельне право
- Історія України
- Кримінально виконавче право
- Медична радіологія
- Методи аналізу
- Міжнародне приватне право
- Міжнародний маркетинг
- Основи екології
- Предмет Політологія
- Соціальне страхування
- Технічні засоби організації дорожнього руху
- Товарознавство продовольчих товарів
Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция
Основи теорії плавання тіл. Закон Архімеда.
На занурене в рідину тіло, що знаходиться в рівновазі, діє сила тяжіння цього тіла і поверхневі сили тиску (рис. 12).
Очевидно, горизонтальні складові сили тиску рідини взаємно врівноважуються.
Розбивши тіло на дві частини: верхню з поверхнею ABC та нижню з поверхнею ADC, визначимо вертикальну складову як алгебраїчну суму сил, які діють на кожну з частин. Величина вертикальної складової сили тиску на криволінійну поверхню дорівнює вазі рідини в об'ємі тіла тиску.

Рис. 12 Сили, які діють на тіло, занурене в рідину.
На частину тіла ABC діє вертикально вниз сила, яка дорівнює вазі рідини в об'ємі AEFCB:
Pz1 = ρ g V1 ,
на частину тіла ADC вертикально вгору діє сила, яка дорівнює вазі рідини в об'ємі AEFCD:
Pz2 = ρ g V2 .
Рівнодіюча цих сил спрямована в бік дії більшої сили - вертикально вгору - і дорівнює вазі рідини в об'ємі ABCD:
Pz = Pz2 - Pz1 = ρ g V2 - ρ g V1 = ρ g V.
Отже, тіло, яке занурене (повністю або частково) в рідину, відчуває з боку рідини сумарний тиск, спрямований знизу вгору і який дорівнює вазі рідини в об'ємі зануреної частини тіла Vзан. Цей тиск називається силою витиснення або підйомною силою: (13)
| P = ρ g Vзан |
Лінія дії сили проходить через центр ваги зануреного об’єму.
Так формулюється закон Архімеда. Силу Р називають архімедовою силою.
Плавучістю тіла називається здатність його плавати при навантаженні. Якщо вага тіла G більше архімедової сили Р (рис. 13, а), то тіло тоне. Якщо G = P (рис. 13, б), то тіло плаває в зануреному стані. Якщо G <P (рис. 13, в), то тіло спливає до тих пір, поки при зменшенні об’єму, який занурений, архімедова сила Р не зменшиться до величини G (рис. 13).

Рис. 13 Типи плавання тіл.
Отже, основна умова плавання тіл виражається так:
G = P = ρ g V (14)
причому під вагою тіла G мається на увазі власна вага плаваючого тіла (корабля, баржі, плота) і вага додаткового навантаження.
Плавання називається підводним при повному зануренні тіла в рідину або надводним при частковому зануренні.
Якщо плаваюче тіло однорідне по всьому об'єму Vт, то його вага дорівнює:
G = ρт gVт
де ρт g - питома вага тіла, Н/м3.
Тоді з умови (14) випливає, що:
 ,
,
або при g = const:
 , (15)
, (15)
тобто відношення питомої ваги плаваючого тіла і рідини зворотно пропорційно відношенню об’єму тіла до об'єму витісненої ним рідини.
При підводному плаванні ці об’єми дорівнюють (Vт = V), отже, умова підводного плавання однорідного тіла виражається рівнянням:
ρт ∙ g = ρ ∙ g (16)
Нехай симетричне тіло перебуває в умовах надводного плавання (рис. 14). Площина, яка перетинає тіло, вільної поверхні рідини називається площиною плавання. Лінія перетину поверхні тіла з площиною плавання називається ватерлінією, а обмежена нею площина - площиною ватерлінії.
Глибину занурення найнижчої точки змоченої поверхні тіла у називають осадкою. Найбільша можлива осадка судна в навантаженому стані звичайно відзначається на ньому червоною ватерлінією. Осадка одного і того ж тіла тим більша, чим менша питома вага рідини.
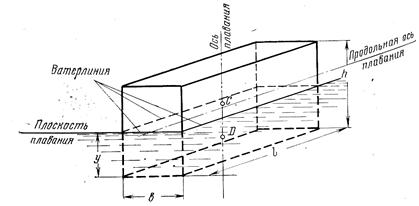
Рис. 14. Надводне плавання симетричного тіла.
Об'єм рідини V, який витіснений тілом, називається об'ємною водотоннажністю, а її вага ρ∙g∙V - водотоннажністю. Водотоннажність судна при повному навантаженні є основною його характеристикою.
Центр ваги об'ємної водотоннажності D, через який проходить лінія дії архімедової сили, називається центром водотоннажності.
Під віссю плавання розуміється лінія, яка проходить через центр водотоннажності D та центр тяжіння С тіла при його рівновазі. Зазначимо, що для збереження рівноваги ось плавання повинна бути вертикальною, інакше сили Р та G складуть пару сил, яка обертатиме тіло.
Остійністю називається здатність плаваючого тіла, яке виведене з рівноваги, повертатися у вихідне положення після припинення дії сил, що викликали крен (нахил).
Розглянемо статичну остійність твердих симетричних тіл, які плавають в спокійній воді, при малих кутах крену (α <15 °).
Тіло може повернутися в нормальне вертикальне положення, якщо пара сил G та Р створює обертаючий момент в бік зменшення крену. В іншому випадку тіло не остійне.
Об'ємна водотоннажність і положення центру тяжіння С для розглянутих тіл не залежить від нахилу осі плавання.
При підводному плаванні (рис. 15) положення центру водотоннажності D не змінюється при крені. Тому можливі два випадки:
1. Центр ваги тіла С знаходиться нижче центру водотоннажності D. Пара сил G та Р прагне знищити крен. Положення тіла остійне.
2. Центр ваги тіла С знаходиться вище центру водотоннажності D. Пара сил прагне збільшити крен. Положення тіла не остійне. Якщо центри С та D співпадають, то при крені тіло перебуває в рівновазі - не повертається в початкове положення, тобто також є не остійним.
При надводному плаванні (рис. 16) при крені центр водотоннажності D переміщується. Остійність тіла також безумовно забезпечується, якщо центр ваги С лежить нижче центру водотоннажності D (рис. 16, а). Якщо ж С лежить вище D, то плавання може бути остійним (рис. 16, б) або не остійним (рис. 16, в).

Рис. 15 Підводне плавання тіла.
Положення центру водотоннажності при надводному плаванні залежить від кута крену, тому що об’єм зануреної частини V, залишаючись постійним за величиною, змінює свою форму. Архімедова сила в новому положенні проходить через центр водотоннажності, який перемістився з нормальної осі плавання в точку D'.

Рис. 16 Надводне плавання тіла при крені.
Положення точки перетину архімедової сили з віссю плавання М також залежить від кута крену. Але при малих кутах (α < 15°) можна вважати положення цієї точки практично постійним. Точка М називається метацентром, а відстань від метацентра М до центру водотоннажності D - метацентричним радіусом r. При невеликому крені центр водотоннажності переміщується по дузі з радіусом кривизни r.
З рис. 16 видно, що якщо метацентр лежить вище центру ваги, пара сил G та Р прагне зменшити крен; якщо метацентр лежить між точками D та С, то пара сил збільшує крен.
Отже, положення тіла є остійним, якщо метацентричний радіус r перевищує відстань між центром ваги і центром водотоннажності (ексцентриситет) δ. І, навпаки, якщо r < δ, то положення тіла не остійне.
Величина метацентричного радіуса при малих кутах крену визначається залежністю:
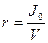 , (17)
, (17)
де V- об’єм зануреної частини;
J0 - центральний момент інерції площі ватерлінії відносно осі, біля якої відбувається поворот.
При кренах навколо поздовжньої осі площини плавання з'ясовується поперечна остійність тіла, при кренах близько поперечної осі - поздовжня остійність.
Очевидно, що поздовжній метацентричний радіус більше поперечного, так як завжди більший момент інерції буде відносно поперечної осі. Тому перевірці підлягає поперечна остійність тіла, яке плаває.
Отже, умову остійності можна висловити нерівністю:
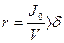 (18)
(18)
або:
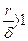 . (19)
. (19)
Чим вище положення метацентра над центром тяжіння, тим більше остійність тіла. Відстань між точками М та С називають метацентричною висотою m. При великому значенні т судно стає хитким. Залежно від призначення судна метацентрична висота приймається в межах m = 0,3...1,2 м.
Лекція № 4 «Основні поняття та рівняння гідродинаміки»
План лекції
1. Основні поняття гідродинаміки
2. Рівняння видатку рідини.
3. Диференційні рівняння руху ідеальної рідини (рівняння Л. Ейлера).
4. Рівняння Д. Бернуллі для елементарного струмочка ідеальної рідини.
5. Рівняння Д. Бернуллі для потоку реальної (в’язкої) рідини.
Читайте також:
- A) правові і процесуальні основи судово-медичної експертизи
- II. Основні закономірності ходу і розгалуження судин великого і малого кіл кровообігу
- IV. Закони ідеальних газів.
- IV. Закономірності структурно-функціональної організації спинного мозку
- R – розрахунковий опір грунту основи, це такий тиск, при якому глибина зон пластичних деформацій (t) рівна 1/4b.
- А .Маршалл - основоположник неокласичної теорії.
- Авілум – “син чоловіка” – повноправна людина, охороні його життя, здоров’я, захисту його майнових інтересів присвячена значна частина законника.
- Аграрне право та законодавство США, Німеччини, Франції, Великої Британії, Ізраїлю, Польщі, Росії
- Аграрні закони України
- Адаптація законодавства України до законодавства ЄС - один із важливих інструментів створення в Україні нової правової системи та громадянського суспільства
- Адаптація законодавства України до законодавства ЄС - один із важливих інструментів створення в Україні нової правової системи та громадянського суспільства
- Адміністративна відповідальність за порушення аграрного законодавства
| <== попередня сторінка | | | наступна сторінка ==> |
| Тиск рідини на циліндричні стінки трубопроводів. | | | Основні поняття гідродинаміки. |
|
Не знайшли потрібну інформацію? Скористайтесь пошуком google: |
© studopedia.com.ua При використанні або копіюванні матеріалів пряме посилання на сайт обов'язкове. |