• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Находження хорд рівноваги і критичної точки

Як видно з рис. 11.7.1, на трикутній діаграмі нанесено, згідно експериментальними даним, невелике число хорд рівноваги. Але в розрахунковій практиці виникає необхідність побудови всередині гетерогенної області будь-яку хорду рівноваги. З цією метою на трикутну діаграму наносять так звану з'єднуючу лінію, як це виконано на рис. 11.7.1.

Для побудови з'єднуючої лінії використовують точки Е і R, Е₁ і R₁, Е₂ і R₂ на обох гілках ЕК і як бінодальної кривої ЕК, яка характеризує рівноважні склади.

Через точки Е, Е₁, Е₂ ... паралельно сторонам MG і ML діаграми проводять лінії побудови до їх перетину в точках С, С₁, С₂, .... як це показано на рис. 10.7.1. Проводячи через точки перетину плавну криву, знайдемо, з'єднуючу лінію СС₁С₂...К, котра перетинає лінію рівноваги в критичній точці змішання К.

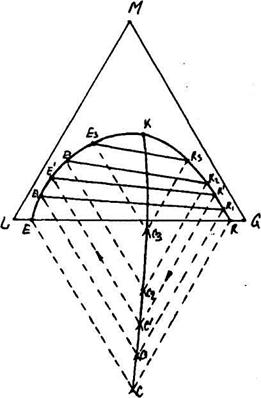
Рис. 11.7.1. Інтерполяція хорд рівноваги.

Для характеристики будь-якої хорди рівноваги, яка проходить через точку R`, на правій гілці рівноважної кривої необхідно провести лінію побудови R`C`, паралельну стороні ML діаграми, до перетину зі з'єднуючою лінією в точці С` Потім з точки С` потрібно провести другу лінію побудови С`Е` паралельно стороні MG діаграми до перетину з лівою гілкою рівноважної кривої в точці Е'. З'єднавши R` і E` прямою лінією, отримаємо шукану хорду рівноваги R'E'. Знаходження хорд рівноваги з допомогою з'єднуючої лінії називається інтерполяцією хорд рівноваги.

Читайте також:

1. Алгебраїчний спосіб визначення точки беззбитковості
2. Алгоритм знаходження ДДНФ (ДКНФ) для даної булевої функції
3. Алгоритм знаходження оптимального плану
4. Алгоритм знаходження початкового опорного плану
5. Аналіз загальної рівноваги
6. Аналіз точки беззбитковості
7. Аналіз часткової рівноваги Крива виробничих можливостей
8. Аналіз часткової та загальної рівноваги
9. Аналіз часткової та загальної рівноваги
10. Будь – які зміни популяції є результатом порушення рівноваги між її біотичним потенціалом та опором довкілля.
11. Виведення формул для знаходження площі паралелограма, трикутника, трапеції. Формули для знаходження площ поверхонь просторових геометричних фігур.
12. Видалення характерної точки

Переглядів: 569