Новини освіти і науки:

G+

Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция

Алгоритми шифрування в електронних картах

Алгоритми шифрування, які використовуються в електронних картах, можна поділити на дві основні групи за типом використаного криптографічного алгоритму. Найпопулярніші серед них подані нижче.

Симетричне шифрування: алгоритм DES; алгоритм 3DES; алгоритм IDEA; алгоритм RC5; алгоритм AES.

Асиметричне шифрування: RSA; ECC; DSS.

Алгоритм шифрування в безконтактних картах.Найрозповсюдженішими безконтактними картами є карти, які виготовляються фірмою Philips, яка розробила два стандарти для своїх карт: MIFARE та HITAG. Найчастіше використовуються карти MIFARE з огляду на їх більшу швидкодію при трансмісії даних та підвищену безпеку.

Для шифрування даних використовується ряд алгоритмів.

АлгоритмDES– один з перших алгоритмів, який використовується в електронних картах. Уперше його використала фірма Philips в електронних картах у 1985 р. На сьогодні його застосовують у модифікованій версії новітніших алгоритмів, тому слід детальніше висвітлити принцип його функціонування.

Шифрування полягає у початковій перестановці бітів 64-х бітового блоку в 16-ти циклах шифрування і кінцевій перестановці. Для опису алгоритму DES використані такі позначення:

L і R – послідовність бітів (ліва і права);

LR – конкатенація послідовностей L і R, тобто така послідовність бітів, довжина якої дорівнює сумі довжин L і R;

– функція за модулем 2 на 48-ми бітовому векторі даних;

А – вхідний блок.

Принцип функціонування алгоритмуDES.З явного вхідного текстового файлу зчитується 64-ох бітовий блок А. Першим кроком є перестановка цих бітів згідно з таблицею початкової перестановки IP. Ці перестановки можна записати як A₀=IP(A). Отриману послідовність бітів A₀ поділяють на дві однакові послідовності: L₀ – ліві біти; R₀ – праві біти.

Наступним етапом є здійснення ітераційного процесу шифрування. Допустимо, А_i – результат і-ої ітерації:

A_i = L_iR_i, (3.1)

L_i=R_i_–1, i = 1, 2, ..., 16, (3.2)

R_i=L_i_–1Å f(R_i_–1, k_i), i = 1, 2, ..., 16, (3.3)

де: f(R_i_–1, k_i) – функція шифрування.

У останньому 16-му циклі отримуємо послідовності R₁₆ та L₁₆.

Алгоритм шифрування завжди закінчується відновленням позиції бітів за допомогою оберненої матриці перестановок IP^–1. Це необхідно для того, аби використовувати цей самий алгоритм як для шифрування, так і для дешифрування. Схема шифрування алгоритму подана на рис. 3.6.

Алгоритм обчислення функціїf.Для обчислення функції f використовуються:

·функція розширення Е, тобто розширення від 32 бітів до 48 бітів;

·функція підстановок S_j, j = 1, 2,…, 8, тобто перетворення 6-ти бітового числа у 4-ох бітове;

функція перестановок Р, тобто перестановка бітів у 32-ти бітовій послідовності.

Рис. 3.6. Схема шифрування алгоритму DES

Алгоритм створення ключа.У кожній ітерації використовується інший новий ключ К_і довжиною 48 бітів. Ключ К_і обчислюється на підставі ключа шифрування К. Ключ К є 64-ох бітовим блоком з 8-ми бітами контролю парності, які розміщені на позиціях 8, 16, 24, 32, 40, 48, 56, 64.

Алгоритм3DES.Цей алгоритм є своєрідною модифікацією алгоритму DES. Відмінність між ними полягає в тому, що повідомлення шифруються три рази алгоритмом DES: зашифровується першим ключем; розшифровується другим ключем; зашифровується третім ключем, зокрема,

c = E₃(D₂(E₁(m))). (3.4)

Дешифрування в другій фазі не впливає на суму алгоритму, але дозволяє застосувати алгоритм 3DES у режимі компатибільності з алгоритмом DES – ключем першим і другим або другим і третім приймаємо такий самий ключ, а останнім – звичайний ключ, як в алгоритмі DES:

c = E₃(D₁(E₁(m))) = E₃(m), (3.5)

c = E₃(D₃(E₁(m))) = E₁(m). (3.6)

Алгоритм 3DES використовує режими роботи та блоки такої самої довжини, як алгоритм DES.

Алгоритм RSA. В цьому алгоритмі випадково Генерується досить велике число – ключ явний, який використовується для обчислення іншого великого числа – приватного ключа за допомогою достатньо складних марематичних функцій. Користувачі застосовують ці ключі для шифрування документів, які висилаються до них двома і більше особами, та для розшифрування документів після їх отримання.

Схема шифрування/дешифрування алгоритму RSA подана на рис 3.7.

Сам алгоритм можна подати наступним чином:

· вибираються два великі прості числа р, q;

· перемножуємо їх n=p×q;

· обчислюємо φ(n)=(p–1)(q–1);

· вибирають випадкове число 1<e<φ(n), яке є простим відносно φ(n);

· використовуємо ключі: явний (публічний) і приватний.

З метою безпечного шифрування та дешифрування слід виконати такі вимоги:

· числа p i q повинні мати по ~100 цифр;

· числа p i q не можуть бути дуже близькими одне від другого.

Алгоритм DSS. Алгоритм DSS – це поточна назва, але якщо йде мова про особливості, то це стандарт цифрових підписів. Ґрунтується він на методі верифікації особи, яка висилає інформацію, та інтегральності переданих даних. Стандарт базується на двох алгоритмах:

· алгоритм Діффі-Хелмана, який призначений лише для узгодження приватного ключа між особами, які надають і отримують інформацію, але не може бути використаний для безпосереднього шифрування даних. Цей алгоритм полягає в обчисленні дискретної експоненційної функції і дискретного логарифму;

алгоритм SHA – це алгоритм безпечного хешування, яке в криптографії має два значення: змішувати і стискувати. У першому значенні вживається для безпечного шифрування текстів (наприклад, в алгоритмі RSA), а в другому – для отримання на підставі тексту певного унікального числа, яке використовується для створення цифрового підпису. Найчастіше використовується така версія, яка характеризується тим, що здійснення операцій в одну сторону є простим, а в іншу – надзвичайно складним. Мова тоді йде про односпрямовану функцію хешування, а відповідний алгоритм має назву SHA-1.

Рис. 3.7. Схема шифрування/дешифрування алгоритму RSA

Алгоритм ECC. Алгоритм ECC (Elliptic Curve Cryptography) базується на еліптичних кривих. Останні дозволяють використовувати менші ключі, що є дуже важливим у банківській справі з огляду на процесори карт.

Беручи до уваги високу швидкодію алгоритму ECC при шифруванні і згадані невеликі ключі, його часто застосовують у безпровідній комунікації, а отже – у безконтактних картах. Для унаочнення переваг цього алгоритму можна сказати, що ключ двійковою довжиною від 150 до 350 знаків, забезпечує таку саму криптографічну стійкість, як ключ від 600 до 1400 і більше знаків в інших криптографічних системах.

Розглянемо загальні поняття еліптичних кривих. Загальне рівняння еліптичної кривої можна подати у вигляді

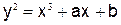. (3.7)

З точки зору криптографії маємо нову криптологічну систему на підставі еліптичних кривих.

Додавання точок P i Q (рис. 3.8):

1. P+0=0+P=P для всіх P ε E (E – еліптична крива);

Якщо P=(x, y) ε E, тоді P+(–P)=0 , де – P=(x, –y);

3. Допустимо, P=(x₁, y₁), Q=(x₂, y₂) ε E де – P≠–Q. Тоді P+Q=(x₃, y₃), причому x₃=λ₂– x₁– x₂(mod p), y₃=λ (x₁– x₃) – y₁ (mod p),

якщо P≠ Q, (3.8)

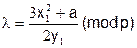якщо P = Q. (3.9)

Рис. 3.8. Додавання точок P i Q на еліптичній кривій

Вимоги до алгоритмів. Крім очевидних вимог, таких як неможливість розшифрування доступними засобами, обчислювальна складність алгоритму повинна бути такою, щоб поміститися в пам’яті карти. При цьому вмонтований процесор повинен здійснити обчислення за короткий проміжок часу.

Декілька обмежень, які накладаються на алгоритми, розроблювані для використаня в електронних картах:

· засоби пам’яті (RAM – 0,5 … 1 Кб; ROM – 50 Кб);

· швидкість передавання даних;

· список розпоряджень процесора і копроцесора;

· можливість генерування ключа приватного і явного (так звана імплементація тестів сильних чисел).

Стосовно вимог безпеки можна використати приклад обчислень для алгоритму RSA. Приймаючи ключ 1024-бітовий, отримуємо, що для зламання шифру потрібні сотні тисяч років навіть для сучасних суперпродуктивних комп’ютерів.

Читайте також:

<== попередня сторінка	\|	наступна сторінка ==>
Система безпеки мікропроцесорних карт	\|

Не знайшли потрібну інформацію? Скористайтесь пошуком google:

Генерація сторінки за: 0.007 сек.