• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Алгоритми побудови дерев екстремальної ваги

(мінімального або максимального)

У комплексі оптимізаційних задач розглядаються графи, кожному ребру чи дузі яких поставлена у відповідність вага.

Алгоритм побудови мінімального (максимального) покривного дерева дуже простий. Спочатку кожна вершина з’єднується з іншою вершиною ребром найменшої (чи найбільшої ваги). Далі кожна вершина з’єднується з вже побудованим фрагментом дерева ребром мінімальної (максимальної) ваги.

На підставі цих принципів розроблений алгоритм Прима та його модифікація - алгоритм Краскала.

Усі сформульовані вище типові задачі розв’язуються абсолютно однаково після формалізації їх у графовому (мережному) вигляді. Можемо застосувати розв’язку різні алгоритми.

Алгоритм Краскала

Алгоритм Краскала використовують для розріджених графів (велика кількість вершин і невелика кількість ребер). Алгоритм складається з таких кроків. Перед початком роботи алгоритму виключаються всі петлі. Вони у побудові дерева брати участь не будуть.

Крок 1. Усі ребра рангуються в порядку зменшення (або збільшення) ваги ребер.

Крок 2. Вводимо до фрагмента побудованого дерева перше ребро із рангового списку.

Крок 3. Розглядаємо наступну пару вершин .

Можливі 3 варіанти:

- одна із вершин входить до фрагмента побудованого дерева. В цьому випадку, ми включаємо це ребро до фрагмента побудованого дерева і переходимо на початок рангового списку;

- обидві вершини входять до фрагменту побудованого дерева. В цьому випадку ми пропускаємо це ребро;

- жодна з вершин не входить до вже сформованого побудованого дерева. Тут ми також пропускаємо ребро.

Крок 4. Алгоритм автоматично завершує свою роботу по побудові дерева з кількістю ребер (n-1).

Алгоритм Прима.

Для повних графів списки стають великими – це не зручно для обробки на ЕОМ, тут більш зручно використовувати матричну форму подання ваги ребер.

В матричній формі використовують модифіковану матрицю суміжності, замість (1 та 0) записуємо вагу ребер. Дана матриця відображає вершини, зв’язки, ваги поставлені у відповідність цим зв’язкам. Цей метод зручний для програмування на алгоритмічних мовах.

Алгоритм Прима працює з матрицею А і використовує матрицю-рядок мінімальних (максимальних) відстаней та індексний рядок, який показує з якого рядка матриці А взято елемент.

S – рядок max (min) відстаней;

І – індексний рядок.

При побудові дерева мінімальної ваги діагональні елементи повинні бути замінені нескінченністю.

При побудові дерева максимальної ваги діагональні елементи будуть 0 (тобто зв`язку немає).

Крок 1.Формуємо допоміжну матрицю, яка складається з матриці-рядка та індексного рядка. Записуємо данні з першого рядка матриці А.

Крок 2. У першому рядку допоміжної матриці вибираємо мінімальну (максимальну) вагу та викреслюємо її. Потім порівнюємо рядок матриці А індекс якого співпадає з індексом стовпчика , який був викреслений. У рядку допоміжної матриці.

Крок 3.Виписуємо з матриці А у допоміжну матрицю: в рядок S - більш мінімальну (максимальну) вагу, а в індексний рядок - індекс рядка з якого були виписані данні. Коли будуть переглянуті усі рядки алгоритм автоматично закінчує свою роботу.

Алгорим знаходження мінімального (максимального) циклу.

До задач знаходження мінімальної або максимальної ваги відноситься задача побудови циклу (контуру).

Цикл (контур), що проходить через всі k вершини графа тільки один раз називається гамільтоновим циклом (контуром). Кількість ребер (дуг), що входять до гамільтонового циклу (контуру) дорівнює k.

Розглянемо задачу. Група іноземних спостерігачів за підготовкою проведення перевиборчої кампанії повинна провести інспекцію в районі. У даному районі k міст, відстань між якими відома. Спостерігачі відправляться із одного із міст з тим, щоб відвідати усі інші (k - 1) місто. Вони повинні побувати в кожному місті один раз з мінімальними затратами часу. Як знайти найкоротший шлях?

Ця задача на побудову гамільтонового маршруту. Наприклад, число маршрутів, які починаються та закінчуються у місті А, дорівнює n = (k - 1)!. Якщо число міст невелика, то повний перебір всіх маршрутів, які починаються та закінчуються у місті А, можемо організувати використовуючи допоміжний граф, який називається граф - деревом.

Для даної задачі k = 5. Заданий граф рис. 14. Буквами A, B, C, D, E позначили міста. Спостерігачі-інспектори починають та закінчують свій маршрут у місті А.

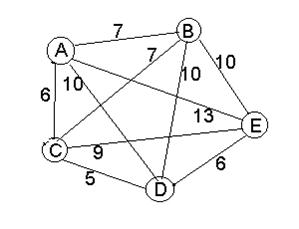
Рис. 14. Наближена схема району.

На рис.15 покажемо граф-дерево, на якому показано 24 можливих маршрути, які починаються та завершуються у місті А. Жирною лінією виділимо самий короткий маршрут та для порівняння лінією виділимо найбільш довгий маршрут.

S_ABEDCA = 7+10+6+5+6 = 34 (самий мінімальний маршрут), S_ACDEBA =34;

S_ADBCEA = 10+10+7+9+13 = 49 (самий максимальний маршрут), S_AECBDA =49.

Як ви вже впевнилися вище викладений алгоритм дуже громіздкий. І все ж таки перебір маршрутів інколи буває корисним.

Але існує метод рішення задач у відповідності з яким крок за кроком будується не повне, а зрізане граф-дерево. Тобто частина гілок у ході його побудови відсікається, а решта гілок ведуть до рішення. Цей метод називається методом гілок та границь.

1.

2.

3.

4.

	Обчислити довжину отриманого матшруту Sm

5. ні

7.

ні

8.

	Кінець

Рис. 16. Блок-схема методу «гілок та границь».

Покажемо рішення задачі знаходження найкоротшого маршруту проведення інспекції спостерігачами у заданому районі. Тобто знайдемо мінімальний гамільтоновий маршрут (цикл). Рішення проведене за блок-схемою (рис.16) та показано на рис. 17.

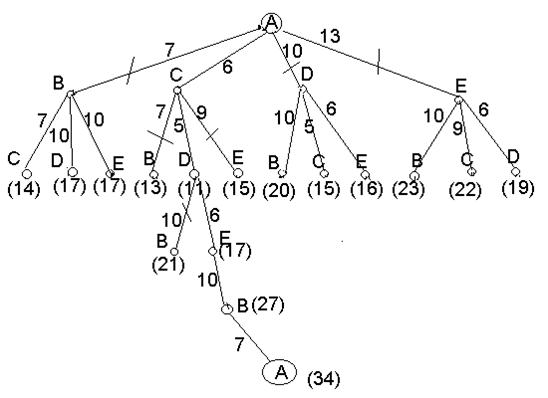
Рис. 17. S _ACDEBA = 34 мінімальний маршрут (гамільтоновий цикл).

Ще раз підкреслимо, що задача про спостерігачів , якщо розуміти її в загальному випадку, є задачею «на графі», тобто дана граф-схема, і на ній необхідно знайти маршрут, який вимагається. Постановка задачі вимагала застосування графа і рішення також вимагає використання графа. Один з найкращих способів рішення засновано на застосуванні графа типа дерева.

Якщо степінь кожної вершини (число ребер, які виходять з неї) графа, який має n вершин повинна дорівнювати r(v_i) ³ 3 , то на цьому графі можемо побудувати гамільтоновий цикл (контур).

Читайте також:

1. Аксіоматичний метод у математиці та суть аксіоматичної побудови теорії.
2. Алгоритм побудови сітьових графіків.
3. Алгоритми
4. Алгоритми арифметичних операцій над цілими невід’ємними числами у десятковій системі числення.
5. Алгоритми групи KWE
6. Алгоритми керування ресурсами
7. Алгоритми переведення чисел з однієї позиційної системи числення в іншу
8. Алгоритми симетричного і асиметричного шифрування
9. Алгоритми та блок-схеми
10. Алгоритми шифрування в електронних картах
11. АРХІТЕКТУРНІ ТРАДИЦІЇ УКРАЇНСЬКИХ ДЕРЕВ‘ЯНИХ ЦЕРКОВ

Переглядів: 3112