• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Методи формування фундаментальних дерев.

Матриці перерізів та контурів.

При вивчені структурних властивостей графів зручно користуватися їх матричними представленнями.

Основні суграфи, які мають велике значення у прикладній області теорії графів - дерева, доповнення, перерізи, контури( цикли).

Базова матрична модель графа - це матриця інцидентності S. Над матрицею інцидентності S можемо проводити еквівалентні перетворення:додавати рядки, переставляти стовпці. Елементи матриць інцидентності неорієнтованих графів можуть бути тільки нулі і одиниці. Тому додавання над елементами виконуються за так званим mod 2(якщо у стовпцю стоїть дві одиниці, то при додаванні рядків даних стовпців, ми отримуємо нуль, але при додаванні рядків у стовпцю яких стоять 0 та 1 ми отримуємо одиницю).

Із n рядків матриці S зв’язного графа один рядок завжди лінійно залежний, тобто ранг матриці S r = n - 1. Число незалежних стовпців матриці інцидентності також дорівнює n - 1, якщо відповідні їм ребра утворюють дерево графа. Решта m - n + 1 стовпців відповідає ребрам, які утворюють доповнення графа.

Якщо необхідно сформувати одне дерево, яке володіє будь-якими властивостями (наприклад, екстремальне дерево), то можемо скористуватися алгебраїчними способами перетворення матриці інцидентності.

Попередньо ребра графа нумеруються. Необхідно вибрати n - 1 стовпців, щоб у сукупності вони були незалежні. Для цього використовуються операції над матрицею інцидентності, не порушуючи рангу матриці.

У результаті в матриці S можемо виділити одиничну матрицю, стовпці якої будуть відповідати гілкам дерева. Якщо використовується матриця S, то в кінці всі елементи останнього рядка перетворюються в нулі і виділяється одинична матриця (n - 1) -го порядку. Ця процедура подібна алгоритму виключення Гауса-Жордана з вибором опорних елементів за стовпчиками.

Приклад.

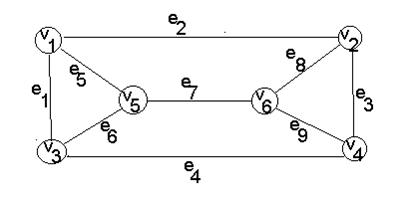
Рис. 18. Граф.

_

S = .

Замінимо перший рядок її сумою з другим рядком по mod 2;

_

S ^I = _.

Замінимо третій рядок її сумою з першим рядком .

_

S ^II = .

Тепер замінимо:

n перший рядок її сумою з третім рядком ;

n другий рядок її сумою з третім рядком;

n четвертий рядок її сумою з третім рядком;

_

S ^III = _.

В перших трьох стовпцях та рядках утворилися елементи одиничної матриці. Але в наступному стовпці неможливо вибрати опорний елемент, так як у решти рядків цього стовпчика стоять нульові елементи. Тому четвертий стовпець пропускається і розглядається п’ятий.

Тепер замінимо:

n другий рядок її сумою з четвертим рядком;

n третій рядок її сумою з четвертим рядком;

n п’ятий рядок її сумою з четвертим рядком;

_

S ^IМ = .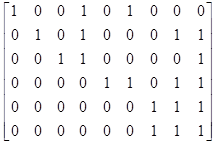

Далі маємо можливість вибрати опорний (ведучий) елемент в сьомому стовпчику. Заміняємо останній рядок її сумою з п’ятим рядком та отримуємо.

_

S ^М = _.

Як і чекали останній рядок перетворився в нульовий його ми можемо відкинути. Маємо п’ять стовпців, в яких є тільки по одному одиничному елементу. Вони складають одиничну субматрицю, а відповідні їм ребра {e₁, e₂, e₃, e₅, e₇} утворюють дерево графа. Решта стовпців {e₄, e₆, e₈, e₉}, відповідають хордам, які утворюють доповнення дерева. Переставимо стовпчики так, щоб з ліва була одинична субматриця. Результат перетворення матриці інцидентності запишемо так:

_

П = .

Сформували фундаментальне дерево, яке покажемо на рис. 19.

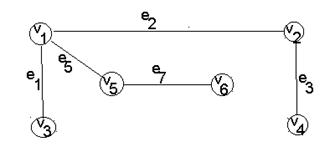
Рис. 19.

Дерево графа визначає множину перерізів, яке представлене в аналітичній формі матрицею П, яка називається матрицею перерізів. Між гілками дерева та перерізами є взаємно-однозначне співвідношення. Тому рядки матриці П будемо позначати номерами тих гілок, які визначають перерізи. Матрицю перерізів можемо представити в канонічній формі яка має вигляд:

П = ,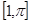

де p - матриця перерізів для хорд розміру (n - 1) ´ (m - n + 1).

Гілка дерева, яка визначає переріз, називається визначаючою гілкою. Різні дерева породжують і різні сукупності незалежних перерізів.

Матриця контурів.

Будь-яка з m - n + 1 хорд утворює сумісно з сукупністю гілок дерева простий цикл. Число s = m - n + 1 називається цикломатичним числом графа.

Головний цикл (контур) - визначається кожною хордою, яка називається визначаючою хордою.

Матриця контурів Р розміру (m - n + 1) ´ m, рядки якої відповідають контурам,, а стовпці - ребрам

_

Р = _ .

Стовпці матриці контурів, відповідні хордам, можемо виділити в одиничну підматрицю.

_

Р = _ .

Таким чином, в канонічній формі матриця контурів має вигляд:

Р = [r, 1],

де r - матриця контурів для гілок дерева розміру (m - n + 1) ´ (n - 1).

Читайте також:

1. Автоматизація водорозподілу на відкритих зрошувальних системах. Методи керування водорозподілом. Вимірювання рівня води. Вимірювання витрати.
2. Агрегативна стійкість, коагуляція суспензій. Методи отримання.
3. АДАПТОВАНА ДО РИНКУ СИСТЕМА ФОРМУВАННЯ (НАБОРУ) ОКРЕМИХ КАТЕГОРІЙ ПЕРСОНАЛУ. ВІДБІР ТА НАЙМАННЯ НА РОБОТУ ПРАЦІВНИКІВ ФІРМИ
4. Адаптовані й специфічні методи дослідження у журналістикознавстві
5. Адміністративні (прямі) методи регулювання.
6. Адміністративні методи - це сукупність прийомів, впливів, заснованих на використанні об'єктивних організаційних відносин між людьми та загальноорганізаційних принципів управління.
7. Адміністративні методи управління
8. Адміністративні, економічні й інституційні методи.
9. Адміністративно-правові (організаційно-адміністративні) методи мотивації
10. Адміністративно-правові методи забезпечення економічного механізму управління охороною довкілля
11. Аерометоди
12. Активні групові методи

Переглядів: 1925