• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Основи моделювання

Закон збереження енергії. Енергія (одиниця вимірювання – джоуль) є найуніверсальнішою характеристикою інтенсивності руху (кінетична енергія ЕК) і взаємодії (потенціальна енергія ЕП) всіх форм матерії. Різні види руху і взаємодії матерії характеризуються різними видами енергії: механічною, хімічною, електричною, ядерною, променистою тощо. Для будь-яких процесів без порушень чи винятків виконується закон збереження енергії: Під час довільних фізичних, хімічних чи інших перетворень речовини у замкнених системах сума всіх видів енергії залишається сталою.

Фундаментальні рівняння типових процесів перенесення в харчових технологіях

И1. 56-80

Базовими для всіх сучасних природничих наук є закони збереження та перетворення енергії і маси.

Закон збереження маси.У процесах, які супроводжуються найрізноманітнішими фізичними та хімічними реакціями, маса початкових і кінцевих речовин однакова, кількість атомів хімічних елементів залишається сталою. Нагадаємо, що міжнародною одиницею вимірювання маси є кілограм.

Типовими для різних схем ХТС є завдання дослідження масових потоків, потоків енергії і окремих компонентів. Диференціальні рівняння цих процесів мають загальну форму:

1. Для завдань транспортування речовини з одного об'єкту в іншій.

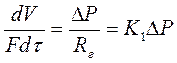
(1)

,

де K₁ – коефіцієнт швидкості; ΔP – рушійна сила процесу (різниця тиску в об'єктах); V – об'єм переміщуваної речовини; τ – час переміщення R_г – гідравлічний опір.

Наприклад, нам треба перемістити молоко з однієї ємкості в іншу. Потрібно створити різницю тиску в цих ємкостях.

2. Для потоку енергії

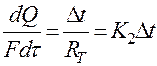
(2)

де Δt – рушійна сила процесу (різниця температур); F – площа поверхні теплопередачі; R_Т – термічний опір; Q – тепловой потік; K₂ – коефіцієнт теплопередачі.

3. Для переходу окремого компоненту з однієї системи в іншу.

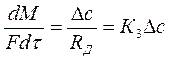
(3)

,

де М – маса компоненту; F – площа поверхні фазового контакту; Δс – різниця концентрацій; Rд – дифузійний опір; K₃ – коефіцієнт швидкості.

Таким чином, узагальнене рівняння перенесення

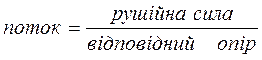
Подібність процесів визначувана виразами (1), (2) і (3), зване «аналогією Колборна», ефективно використовують в моделюванні.

Так, математичний апарат, який апробований в завданнях фільтрування, в теорії електричних ланцюгів, можна успішно використовувати при моделюванні теплових і дифузійних процесів.

Спробуємо виявити універсальні математичні описи для основних видів процесів. Відомо, що перетворення сировини на продукт, як правило, передбачає реалізацію процесів енерго- масообміну. Отже, потрібно знайти універсальні математичні описи саме цих процесів.

Розглянемо один з найскладніших процесів, пов'язаних із споживанням механічної енергії, - процесу руху потоку рідини (газу).

Цей процес зустрічається повсюдно і пов'язаний як з переміщенням самого оброблюваного продукту, так і з переміщенням енергоносіїв (тепло- і хладагентов). Універсальний математичний опис такого процесу існує і носить назва рівняння Навьє-Стокса (4). Воно описує розподіл вектора швидкості кожної частинки рідини в просторі і в часі. Рівняння формою дуже складне, це диференціальне рівняння у векторній формі. Для спрощення наший завдання розглянемо одне з трьох рівнянь – в проекціях на одну з координатних осей Х.

=

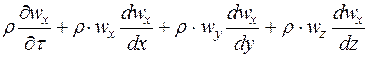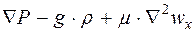
(4)

Позначення: wx, wy, wz – проекція вектора швидкості на осі відповідних координат:

ρ – густина, кг/м³;

Р – тиск, Па;

g – прискорення вільного падіння, м/с²;

μ – динамічний коефіцієнт в'язкості, Па.с;

t – поточний час, с.

Природно, всі члени рівняння мають одну і ту ж розмірність Н/м³. якщо розділити всі члени рівняння на щільність, то отримаємо нову розмірність м/с², це розмірність прискорення. Отже, в правій частині рівняння представлено: зміна швидкості в часі (1 член), зміна проекції швидкості по координатах, з урахуванням того, що ці координати самі рухаються (wx, wy, wz).

=

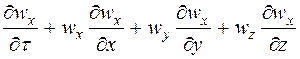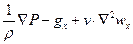
(5)

До складу формули входять оператори 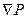і, 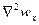які при розгортанні мають наступний вигляд

=

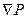(6)

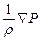– складова прискорення, яка визначається дією сил тиску

g_х – складова, визначувана дією сил тяжіння

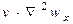– дія сил вязкостного опору в потоці.

Таким чином, поле швидкостей однозначно визначається дією прийнятої системи сил в рухомій, нестаціонарній системі відліку. Це найбільш загальний випадок руху. У міру ухвалення деяких допущень можна спростити початкове рівняння: привести його до стаціонарної форми (), звести рівняння до одновимірного або двовимірного вимірювання (wy = wz = 0). Іншими словами, спільність рівняння велика, воно описує величезний клас процесів, пов'язаних з перебігом рідини під дією системи сил. На цьому переваги універсальної форми закінчуються. Далі слідують її недоліки, які виявляються дуже серйозними.

Приведене рівняння (а тим більше повна система рівнянь для трьох проекцій швидкості) є диференціальним рівнянням другого порядку, в часткових похідних, нестаціонарне. Навіть за умови постійності коефіцієнтів воно не має загального рішення. Окремі рішення, після значних спрощень можливі на ЕОМ із застосуванням чисельних методів, тобто результат кожного разу буде отриманий у вигляді набору цифр, але не аналітичних виразів, що значно утрудняє подальший аналіз рішення і його введення до складу математичної моделі.

Підведення енергії до рухомої рідкої системи описується добре відомим рівнянням енергії, яке має вигляд

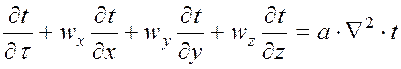
(7)

, (4.28)

де t – температура;

a – коефіцієнт температуропровідності, м²/с; ;

l – коефіцієнт теплопровідності, Вт/(м К);

r – густина;

Ср – ізобарна теплоємність, Дж/(кг.К).

Всі члени рівняння мають одну і ту ж розмірність, К/с.

Рівняння описує розподіл температури в часі і просторі, тобто найбільш загальний випадок, що зустрічається при перенесенні теплової енергії в рухомому середовищі.

Це рівняння також включає оператора Лапласа.

Представлена залежність відноситься до рівнянь математичної фізики, це рівняння в приватних похідних, другого порядку, нестаціонарне і загального аналітичного рішення не має (так само як і попереднє рівняння).

Рівняння конвективного масопереносу (зміна маси речовини (або його концентрації) в потоці рухомої рідини) має вигляд

=

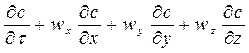(8)

тут с – концентрація речовини в потоці

D – коефіцієнт дифузії, м²/с.

Рівняння описує нестаціонарний (змінний в часі) розподіл концентрації в потоці рухомої рідини.

Очевидний повний формальний збіг цієї залежності з попередніми. Висновок щодо можливості отримання загального рішення для цього рівняння такий же. Загального рішення немає.

Як бачимо реальні об’єкти і явища матеріального світу дуже складні. Людська свідомість не в змозі охватити усі властивості цих об’єктів и зв’язки між ними. З цієї причини в процесі описання та вивчення реальних об’єктів людині доводиться спрощувати їх властивості, тобто заміняти реальні об’єкти їх моделями. В широкому розумінні будь який образ любого об’єкту, в тому числі й уявний, називають моделлю. Моделюванням називають цілеспрямоване дослідження явищ, процесів або об’єктів шляхом складання та вивчання їх моделей. В процесі моделювання складний об’єкт що досліджується — оригінал замінюється іншим, більш простим об’єктом — моделлю.

Моделювання є старим як світ. Наприклад геометричні моделі які передають зовнішні признаки об’єкта: розміри, форму, колір. Це об’єкти геометрично подібні оригіналу. Вони використовуються для учбових та демонстраційних потреб, для проектування та конструювання. З раннього дитинства ви зустрічаєтесь з іграшками які є простими моделями реальних об’єктів навколишнього середовища. При тому моделювалися не тільки окремі предмети але й системи. Так Фалесу Мілетському, який жів у 6ст. д.н.е. приписують метод вимірювання відстаней до кораблів на морі де реальна система з двох спостерігачів та корабля замінялась моделлю, що представляє з себе подібний трикутник

Будь який метод інженерного розрахунку або наукового дослідження базується, власне кажучи, на ідеї моделювання. Які ж переваги від використання моделей.

1.моделювання необхідне при розгляді великого числа варіантів розрахунку з метою одержання компактної, ефективної в енергетичному й економічному плані, надійній конструкції; чи для побудови на основі використання доступного устаткування нової технологічної лінії (цеху, заводу й ін.); математичні моделі при розрахунках дозволяють обробити велика кількість інформації, зіставити по основних параметрах велике число варіантів. Виконати цей обсяг роботи вручну, навіть із застосуванням мікрокалькуляторів, можна зусиллями тільки колективу проектувальників у великий термін. Однак, крім виграшу в часі використання ММ дає й інша перевага: з'являються якісно нові можливості для поліпшення результатів проектування.

2. Використання ММ у науково-дослідній роботі при фізичній неможливості провести експеримент у натурі, чи якщо його проведення технічно складно, дорого і нерентабельно, приймають наступну схему: будують математичну модель досліджуваного процесу максимально використовуючи уже відомі математичні описи, формули й ін., що із прийнятною точністю описують окремі фази, фрагменти, деталі досліджуваного процесу, установлюють припустимі чи можливі границі для варіювання параметрів, що визначають течію процесу. Потім, використовуючи можливості сучасної ЕОМ «програють» можливі варіанти течії процесу по заздалегідь наміченому плану, отримана інформація обробляється також із застосуванням ЕОМ, причому на цьому етапі можливі різні критерії оцінки отриманих результатів (звичайно справа зводиться до пошуку оптимальних режимів, параметрів і ін.).

3. Застосування ЕОМ у системах керування й автоматики. Математична модель процесу (чи його фрагментів) є обов'язковою складовою частиною програмного забезпечення системи керування і є фактичною основою побудови систем моніторингу, визначення робочих характеристик складових частин системи автоматизованого керування (перехідні функції, рівні керуючих впливів і ін.), а так само для вироблення і реалізації керуючих впливів з урахуванням реалізації різних видів зворотних зв'язків.

4. Застосування ММ для рішення задач оптимізації.Число задач, у яких потрібно визначити, оптимальні параметри якого-небудь процесу, конструкції й ін. безупинно росте. ММ звичайно є основою для проведення процесу оптимізації, оскільки практично всі методи оптимізації є математичними (чи засновані на певних математичних положеннях). Задачі оптимізації стали особливо необхідними в умовах, коли чи рано пізно будь-яке технічне рішення проходить т.зв. економічну перевірку. Діапазон задач величезний – від найпростіших – у який враховується зміна одного чи двох параметрів, до складних систем, у яких одночасно можуть змінюватися десятки параметрів.

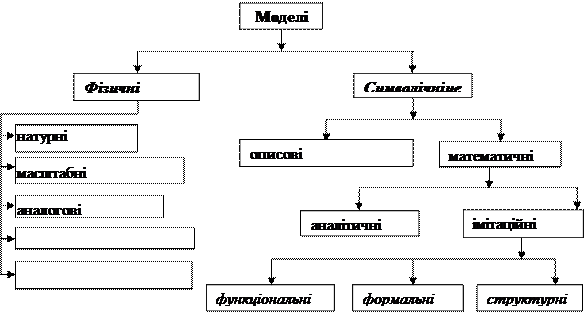
Рис. 1. Класифікація моделей.

Ми розглянули тільки основні галузі, у яких ММ знаходять широке і повсякденне застосування, розглянути всі можливі варіанти використання ММ у нас немає можливості. На закінчення необхідно зробити одне важливе зауваження: не слід думати, що для кожного з розглянутих розділів необхідно створювати власну математичну модель. Це не так. Гарна ММ (та, котра правильно і з достатньою точністю відображає розглянутий процес) може бути основою при рішенні практично будь-якої задачі. При цьому можуть змінюватися: постановка задачі – різні цілі, можуть змінюватися вихідні і граничні умови, можуть з'являтися умови сполучення розв'язуваної задачі з іншими обмеженнями або умовами; при цьому основна ММ залишається незмінною основою програми.

Модель – відображення в деякий формі найсуттєвіших характеристик об’єкта оригінала. В інженерній практиці об’єктами оригіналами є антропогенні технічні об’єкти. Их моделі поділяються на фізичні та символічні. Також ММ можна умовно розділити на дві великі групи: детерміновані і стохастичні (вероятностные) ММ. Кожна з цих груп може включати різні за своєю формою. Відмітною ознакою цих груп є наступне:

ДЕТЕРМІНОВАНІ МОДЕЛІ - від латинського «детермінанта» - визначник. У ММ цього класу при використанні достовірних вихідних даних і правильного (технічно) рішення виходить однозначно визначений (звідси і назва) результат. Найпростішим прикладом служить процедура рішення квадратного рівняння, що зводиться до перебування коренів рівняння по певному алгоритму і результат, якщо він існує, буде однозначно визначений. Те ж можна сказати і про алгоритм рішення рівняння третього ступеня. Саме поняття «визначник» було введено при рішенні систем рівнянь (правило Крамера).

СТОХАСТИЧНІ МОДЕЛІ - їхня принципова відмінність від ММ першого виду полягає в тому, що вихідні дані (або їхня частина) представляються у вигляді вірогідністних співвідношень, а при рішенні використовується математичний апарат теорії імовірностей. Відповідно до цього, результат буде являти собою теж вірогідністне вираз. Незважаючи на удавану складність і незручності в порівнянні з детермінованою моделлю, стохастичн моделі володіють низкою серйозних переваг.

Справа в тім, що вірогідність і однозначність результатів, що дає детермінована модель, є удаваною. Оскільки вихідні дані завжди задаються з відомими допущеннями, а розрахункові залежності найчастіше є наближеними, те і кінцевий результат, по суті, приблизний.

По способу одержання ММ поділяються на наступні групи:

Аналітичні моделі. Утворюються на основі строгих математичних описів, що є результатом чисто аналітичного рішення.

Експериментальні ММ. Утворюються на основі ММ, побудованих у результаті обробки експериментальних даних, як правило, у вигляді критериальных співвідношень.

Змішані ММ (сполучення перших двох груп).

У залежності від форми представлення можуть бути аналітичні, цифрові, аналогові та комбіновані.

(*При цьому розрізняють теоретичні методи, для яких використовуються різного роду знакові, абстрактні моделі, і експериментальні методи, для яких використовують фізичні моделі. Фізичне моделювання припускає проведення реального фізичного експерименту або побудову макета, що імітує реальний експеримент. У ряді випадків фізичне моделювання вимагає створення складних і дорогих установок, що не завжди виправдано. Більш того, фізичне моделювання не завжди дозволяє вивчити внутрішні, сховані від очей спостерігача властивості реальних систем.*)

Процедура створення та використання математичних моделей називається математичним моделюванням. Яке може бути аналітичним та імітаційним.

Вигляд і форма математичної моделі визначаються задачами дослідження і природою досліджуваного об'єкта. Проте, у будь-якому випадку порядок складання математичної моделі можна представити алгоритмом, структурна схема якого показана на мал. . Складання математичної моделі припускає ряд етапів: постановка задачі дослідження; вибір показників якості рішення задачі; визначення і вибір параметрів процесу (системи), що впливають на обрані показники якості; виявлення існуючих зв'язків між параметрами; встановлення і запис математичних залежностей між параметрами; складання математичного опису об'єкта; визначення області рішень (обмежень); складання алгоритмів і програм для вирішення на обчислювальних машинах; оцінка й узагальнення результатів моделювання. Найбільш важливим і найменш формалізованим є перший етап. Постановка задачі дослідження і вибір показників якості рішення грають дуже важливу роль тому що невдачі частіше обумовлені нечітко поставленою задачею або невдалим вибором показника, що не відповідає меті дослідження. Наступних три етапи складання математичної моделі є власне кажучи збором необхідної інформації про об'єкти. Тут необхідно визначити всі параметри об'єкта й існуючі між ними зв'язки на основі законів фундаментальних наук, різних гіпотез і допущень, a також використання експериментальних даних.

Теоретичні основи технологічних процесів вивчаються звичайно по різних опублікованих і рукописних джерелах. Якщо для встановлення зв'язків між параметрами об'єкта не вдається 'підібрати задовільну теорію, тоді висувають гіпотези, справедливість яких перевіряють порівнянням результатів рішень, отриманих на основі прийнятих гіпотез і по експериментальним даним. У такий же спосіб перевіряють справедливість застосування різних теорій. Невелика витрата часу на таку перевірку є одним з переваг аналітичного підходу до дослідження процесів.

Після одержання інформації шляхом перегляду літератури, аналізу документів і звітів, підготовки апріорного даних, аналізу експериментального даних, опитування і консультацій з фахівцями й експертами її варто систематизувати й оцінити з погляду поставленої задачі дослідження. У більшості випадків тільки деяка невелика частина інформації є необхідною і її варто відділити від непотрібної і випадкової. Оскільки зібрана інформація не завжди зручна для безпосереднього використання, її піддають попередній обробці, аналізу й групуванню. Одержати повну інформацію у всіх випадках практично неможливо.

При неможливості одержання інформації або її використань її заміняють іншими даними. Джерелами інформації можуть бути: постановка експерименту в лабораторних або виробничих умовах, висування різних, чітко сформульованих гіпотез, припущень і ін.

• На другому і третьому етапах складання моделі одержують структурну і параметричну схеми. При цьому установлюють важливість і вплив кожного параметра на рішення задачі. Кожний параметр у параметричній схемі описують у наступному порядку: визначення і символ, одиниці для розрахунку, діапазон вимірів, характеристики (одне- і багатозначний, кодований, керований, випадковий і ін.), місце застосування в моделях, джерело параметра і примітки. Параметричний опис є найпростішою формою, заснованою на емпіричних спостереженнях властивостей, ознак і відносин досліджуваного об'єкта.

* У результаті четвертого етапу моделювання одержують вихідні математичні зв'язки між параметрами у вигляді таблиць, графіків, математичних формул, статистичних даних і т.д. На цьому ж етапі записують системи вихідних математичних рівнянь, отриманих на основі обраної фізичної моделі, тобто сформованих представлень про реальний технологічний процес (концептуальна модель).

* На п'ятому етапі визначають область рішення задачі, що у найбільш простих випадках часто зводять до визначення початкових і граничних умов. У загальному випадку обмеження представляють у вигляді нерівностей.

* На шостому етапі вихідні дані і рівняння перетворюють таким чином, щоб форма запису була придатна для рішення поставлених задач. Табличні, графічні і статистичні дані обробляють і представляють у вигляді математичних формул При цьому по можливості спрощують отримані вихідні рівняння шляхом виключення незначущих членів, а іноді і виключенням цілих рівнянь у випадку незначного їхнього впливу на рішення поставленої задачі.

• На сьомому етапі роблять вибір методу рішення отриманих математичних рівнянь у залежності від задачі і рівня дослідження і складності рівнянь. Відповідно до обраного методу рішення роблять необхідні перетворення і заміни в системах рівнянь. Обчислювальній стадії повинен передувати аналіз інформації, яку необхідно одержати за допомогою моделі, з метою виявлення надлишкових ситуацій, що дозволить спростити обчислювальну процедуру. На цьому ж етапі складають чітку послідовність рішення задачі — алгоритм.

• Восьмий етап — складання програми рішень — обумовлюється як попередніми етапами моделювання, так і типом обчислювального пристрою. Програму рекомендується будувати по модульному принципу, тобто у вигляді сукупності стандартних блоків — модулів. Цей шлях досить ефективний, логічно виправданий і може бути порівняно легко здійснений і проведений. Модуль охоплює типову процедуру або стандартний оператор обробки інформації на ЕОМ. Після перевірки програми на логічність і правильність використовуваних рівнянь можна приступити до переведення всіх математичних формулювань на мову машини, а після налагодження програми — до обчислень.

. Ha останньому дев'ятому етапі роблять оцінку й аналіз результатів обчислень. На підставі аналізу видають рекомендації і повідомляють про раніше невідомі факти. Оскільки у вихідних рівняннях можуть бути різні постійні коефіцієнти, обов'язково планують проведення експериментів на моделі. З плану експериментів виводять кількість вихідних даних і визначають метод їхнього аналізу. Необхідно передбачити, яка частина розрахункових даних буде видаватися на друк. Вихідна печатка повинна містити перелік вихідних і вихідних даних з відповідними позначеннями і розмірністю. Наприкінці останнього етапу моделювання складають звіт, що повинний бути змістовним, ясним, точним і повним і включати чисельні значення вихідних даних або спосіб їхнього визначення (план експерименту й ін.), вихідні дані по всіх циклах обчислень, короткий виклад, аналіз і оцінки результатів, висновки і рекомендації з удосконалювання моделі і можливості її застосування.

И1 с 9-23

Читайте також:

1. A) правові і процесуальні основи судово-медичної експертизи
2. R – розрахунковий опір грунту основи, це такий тиск, при якому глибина зон пластичних деформацій (t) рівна 1/4b.
3. Активне управління інвестиційним портфелем - теоретичні основи.
4. Алгоритм моделювання систем масового обслуговування
5. Аналiз ризику методами iмiтацiйного моделювання
6. Аналіз ризику через моделювання.
7. Анатомо-фізіологічні основи статевого розвитку.
8. Бізнес-моделювання в системі управління розвитком підприємства. Поняття та етапи формування бізнес-моделі
9. Біологічні основи мислительної діяльності.
10. Біомеханічні основи шинування при пародонтозі.
11. Біохімічні основи розвитку витривалості
12. Біохімічні основи розвитку силових і швидкісних якостей

Переглядів: 2100