• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция

Розв’язування

Приклад виконання задачі 7

Коротка чавунна колона (чавун СЧ 12) заданого поперечного перерізу (рис.1.6) стискається силою Р, що прикладена в точці Р. Виконати розрахунок колони згідно з приведеним в задачі 7 порядком виконання.

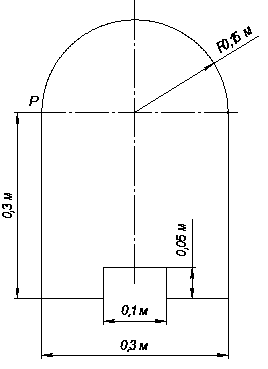
Рис. 1.6. Схема до прикладу задачі 7

Дано:

чавун СЧ 12,

a = d = 0,3 м.

Знайти:

Р_max, 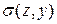, ядро перерізу -?

1. Обчислюємо геометричні характеристики заданого перерізу

Координати центра ваги перерізу

Оскільки фігура має вісь симетрії то центр ваги буде лежати на цій осі ().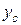

Представимо дану складну фігуру у вигляді комбінації трьох простих : півкола (1) квадрата (2) та прямокутника з від’ємною площею (3) (рис. 1.7). Індекси вказують належність позначення до відповідної фігури.

Площі цих фігур

;

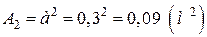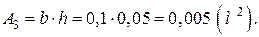
Загальна площа фігури

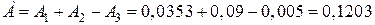(м²).

Проведемо допоміжну вісь z. Відстані від координат центрів ваги цих площ до вісі z

;

;

.

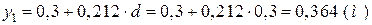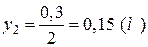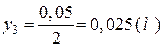Шукаємо координату 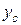фігури до допоміжної вісі z.

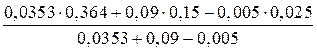== 0,218 (м).

Проводимо вісь z_с яка разом з віссю y_с утворює систему головних центральних осей

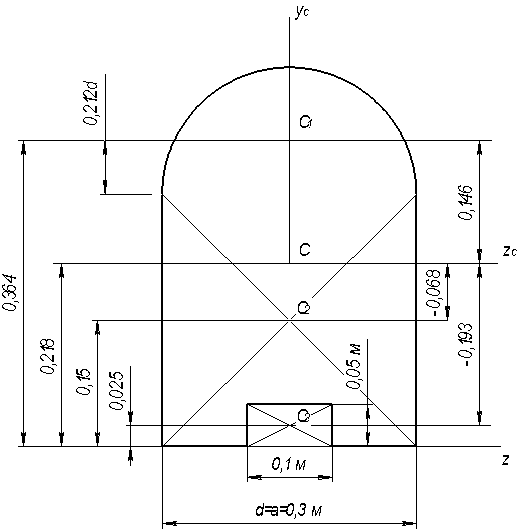
Рис. 1.7. Визначення центра ваги перерізу

1.2 Визначаємо головні моменти інерції перерізу

Моменти інерції окремих фігур в їхніх центральних осях

J_z1 =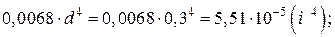

J_y1 =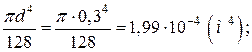

J_y2 = J_z2 =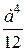= = 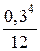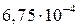(м⁴);

J_z3 = =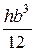

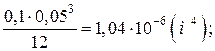
J_y3 = =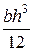

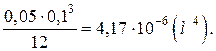
Знаходимо координати центрів ваги С₁(a₁; b₁), С₂(a₂; b₂) та С₃ (a₃; b₃) в системі центральних осей z_с – y_с.

a₁ = a₂ = a₃ = 0 (м),

b₁ = y₁ – y_c = 0,364 – 0,218 = 0,146 (м),

b₂ = y₂ – y_c = 0,15 – 0,218 = -0,068 (м),

b₃ = y₃ – y_c = 0,025 – 0,218 = -0,193 (м).

Центральні осьові моменти інерції перерізу

J_zс = J_z1 + b₁² ×А₁+ J_z2 + b₂² ×А₂ – J_z3 – b₃² ×А₃ = 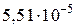+0,146²×0,0353+ +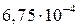+ (-0,068)²×0,09 – 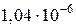– (-0,193)²*0,005 = 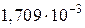(м⁴);

J_ус = J_у1 + a₁² ×А₁+ J_у2 + a₂² ×А₂ – J_y3 – a₃² ×А₃ =

= J_у1 + J_у2 – J_y3 =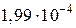+ 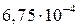– 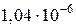= 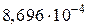(м⁴);

1.3 Визначаємо головні радіуси інерції перерізу

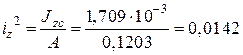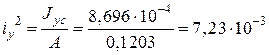(м²);

(м²).

2. Будуємо нейтральну лінію та визначаємо небезпечні точки перерізу

Будуємо нейтральну лінію через відрізки, які вона відсікає на головних осях

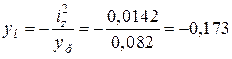(м);

(м);

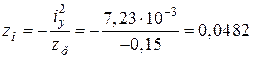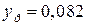де (м), 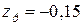(м) – координати точки прикладення сили Р в системі головних центральних осей z_с – y_с.

Відкладаємо в масштабі отримані відрізки 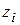та 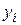на осях та проводимо нейтральну лінію (рис. 1.8).

Небезпечні точки перерізу є найвіддаленішими від нейтральної лінії. Це точки А і В (рис. 1.8). Координати цих точок в системі z_с – y_с

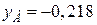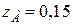т. А (точка максимального розтягу „+”) (м), (м);

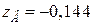т. В (точка максимального стиску „-”) (м), (м).

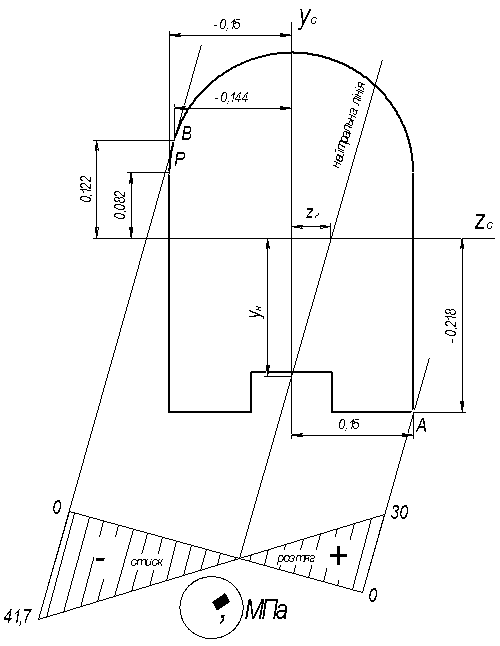
Рис. 1.8. Епюри нормальних напружень

3. Максимальне значення сили Р

3.1 Визначаємо допустимі напруження матеріалу стержня

Для чавуна СЧ 12 границі міцності при розтягу і стиску відповідно 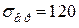МПа, 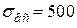МПа (додаток Б, таблиця Б.5).

Задамося запасом міцності n = 4 (орієнтовні межі 3…5 для крихких матеріалів).

Допустимі напруження матеріалу становлять

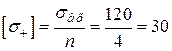(МПа);

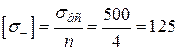(МПа).

3.2 Визначаємо максимально допустиме значення сили Р за умов міцності

;

.

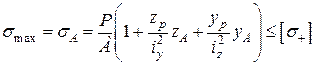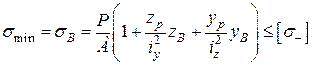Звідки

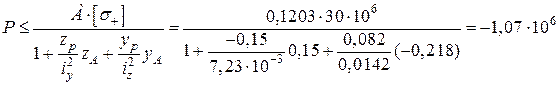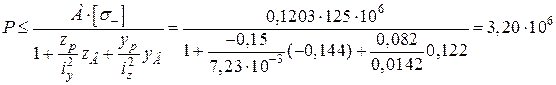(Н);

(Н).

Приймаємо меншу за модулем силу:

Р_max = 1,07 МН.

3.3 Будуємо епюру нормальних напружень в перерізі

Оскільки ця епюра лінійна, то достатньо визначити напруження в двох точках, зокрема в точках А та В. При прийнятій силі Р = -1,07 МН (знак „-” показує, що вона стискаюча)

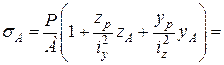
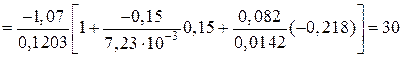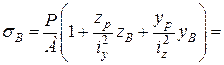
(МПа);

(МПа).

Будуємо епюру за отриманими значеннями, відкладаючи в масштабі відрізки (рис. 1.8) та візуально перевіряємо чи перетинає епюра нейтральну лінію в нулі.

3.4 Будуємо ядро перерізу

Проводимо характерні дотичні 1-1, 2-2 ... (нейтральні лінії) до перерізу. По координатам перетину з головними осями 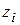, 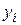визначаємо координати точки 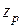, 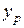прикладення сили Р, при якій буде реалізована ця дотична.

Використовуємо формули

; .

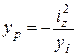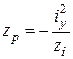Для зручності результати обрахунків приводимо в вигляді таблиці 1.2

Таблиця 1.2

лінія	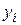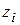, м	, м	точка	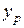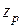, м	, м
1-1	-0,218	¥	Р1	0,065
2-2	¥	-0,15	Р2		0,048
3-3	0,294	-0,294	Р3	-0,048	0,025
4-4	0,232	¥	Р4	-0,061
5-5	0,294	0,294	Р5	-0,048	-0,025
6-6	¥	0,15	Р6		-0,048

З’єднуємо послідовно точки Р₁, Р₂, ... Р₆ та заштрихуємо отриману область (рис. 1.9). Ядро перерізу побудовано.

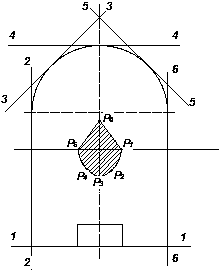
Рис. 1.9. Побудова ядра перерізу

Питання до захисту розрахунково-графічної роботи (задача 7)

1. Записати рівняння нейтральної лінії при позацентровому розтягу-стиску.

2. Записати умову міцності при позацентровому розтягу-стиску.

3. Чому при позацентровому розтягу-стиску зазвичай записують дві умови міцності?

4. Визначити напруження в вказаній точці, використовуючи аналітичний та графічний (з епюр) способи.

5. Побудувати нейтральну лінію, якщо сила Р прикладена в вказаній точці.

6. Що таке ядро перерізу?

7. Для чого потрібно будувати нейтральну лінію?

8. В якій системі координат визначаються координати точок, що входять в розрахункові формули умов міцності?

9. В яких елементах конструкцій реалізуються деформації позацентровому розтягу-стиску – навести приклади.

10. За яким алгоритмом виконують розрахунки стержня при позацентровому розтягу-стиску?

Читайте також:

1. Алгоритм розв’язування задачі
2. Алгоритм розв’язування задачі
3. Алгоритм розв’язування задачі
4. Алгоритм розв’язування задачі
5. Алгоритм розв’язування задачі
6. Алгоритм розв’язування задачі
7. Алгоритм розв’язування задачі оптимізації в Excel
8. Графічний метод розв’язування задач лінійного програмування
9. Завдання для самостійного розв’язування
10. Загальна характеристика методів розв’язування цілочислових задач лінійного програмування
11. Застосування перетворення за Лапласом для розв’язування диференціальних рівнянь
12. Застосування рівнянь та їх систем до розв’язування текстових задач.

Переглядів: 596