• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Основні гіпотези міцності

Оцінка міцності при складному напруженому стані

ТЕОРІЇ МІЦНОСТІ

При лінійному напруженому стані, коли діє тільки одне головне напруження (при розтяганні) або (при стисканні), умова міцності записується у вигляді

s ₁ £ [s]_р або s₃ £ [s]_с

де [s]_р і [s]_с - допустимі напруження відповідно при розтяганні і при стисканні, які встановлюються залежно від величини граничного напруження для даного матеріалу.

Граничне напруження (границя текучості для пластичних матеріалів або границя міцності для крихких) у цьому випадку легко може бути знайдене експериментально в дослідах на розтягання або стискання.

Значно складніше оцінити міцність при складному напруженому стані. Настання небезпечного стану в цьому випадку залежить не тільки від абсолютних величин головних напружень, а також від їх співвідношень. Для оцінки міцності при складному напруженому стані лабораторним шляхом потрібно виконати дуже багато складних випробувань зразків з метою реалізації різних величин і співвідношень головних напружень, що практично здійснити не можливо.

Щоб можна було судити про міцність при складному напруженому стані, треба знати істинні причини руйнування матеріалу. Ці теорії дають можливість скласти умови міцності при складному напруженому стані, виходячи з даних про міцність матеріалу, одержаних з випробувань на просте розтягання або стискання.

Напружені стани при складному напруженому стані і при одноосному розтяганні називатимемо рівнобезпечними або еквівалентними, якщо при пропорційному збільшенні головних напружень в одне і теж число разів вони одночасно стають граничними. Інакше кажучи, коефіцієнти запасу міцності для еквівалентних напружених станів однакові.

Еквівалентним напруженням називають таке умовне напруження одноосного розтягування, яке рівнобезпечне заданому випадку складного напруженого стану.

Відповідно до гіпотез міцності виводять формули для розрахунку еквівалентного напруження, яке потім порівнюють з допустимим напруженням на розтягання. Таким чином умова міцності матиме вигляд

s_екв £ [s]_р (4.1)

Теорія найбільших нормальних напружень (перша теорія міцності). В основі цієї теорії лежить припущення, що причиною руйнування матеріалу є найбільші нормальні напруження. За цією теорією складний і простий напружений стани є рівнобезпечними, якщо найбільші за абсолютною величиною головні напруження у них однакові.

Для матеріалів, які не однаково чинять опір розтяганню і стисканню умови міцності такі:

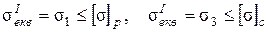(4.2)

де [s]_р і [s]_с - допустимі напруження відповідно при розтяганні і при стисканні.

Перша теорія підтверджується дослідами над невеликою кількістю видів напруженого стану крихких матеріалів. Зараз вона майже не застосовується

Теорія найбільших лінійних деформацій (друга теорія міцності). В основі цієї теорії лежить припущення, що міцність матеріалу при будь-якому напруженому стані визначається величиною максимальних відносних деформацій. За цією теорією складний і простий напружений стани є рівнобезпечними, якщо найбільші відносні лінійні деформації у них однакові.

Позначимо максимальну відносну деформацію при складному напруженому стані 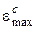, а при простому - через . Тоді умова міцності запишеться у вигляді

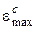£ (4.3)

Використовуючи (3.11) і (2.8) отримаємо

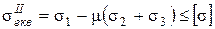(4.4)

Хоча теорія найбільших деформацій і враховує всі три головні напруження, для пластичних матеріалів вона на практиці не підтверджується. Для крихких матеріалів тільки при s₁ > 0 і s₃ < 0 і , якщо при цьому çs₁ç > çs₃ç (за абсолютною величиною), ця теорія наближено узгоджується з даними дослідів.

Першу і другу теорію практично не застосовують.

Теорія найбільших дотичних напружень (третя теорія міцності). В основі цієї теорії лежить припущення, що причиною руйнування матеріалу є дотичні напруження. Отже, граничний стан матеріалу настане тоді, коли максимальне дотичне напруження досягне значення, при якому з'являються пластичні деформації або руйнування цього матеріалу при простому розтяганні або стисканні. Таким чином, за цією теорією простий і складний напружені стани є рівнобезпечними, якщо їх максимальні дотичні напруження дорівнюють одне одному.

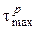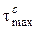Позначимо максимальні дотичні напруження при простому і складному напружених станах відповідно через і . Тоді умова рівнобезпечності, згідно з розглядуваною теорією виразиться рівністю

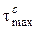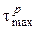= (4.5)

При одноосному розтяганні s_max = s₁, а s₂ = s₃ = 0, а тому згідно з (3.8) максимальне дотичне напруження

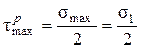(4.6)

При об'ємному напруженому стані

(4.7)

Якщо позначити допустиме напруження при простому напруженому стані , то умова міцності при складному напруженому стані виразиться формулою

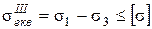(4.8)

Недоліком цієї теорії є те, що вона не враховує впливу проміжного головного напруження .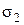

Ця теорія досить добре узгоджується з даними дослідів для пластичних матеріалів, для яких допустимі напруження на розтягання і стискання можуть бути взяті однаковими.

Енергетична теорія міцності (четверта).

Ця теорія грунтується на припущенні, що вирішальним фактором міцності є величина потенціальної енергії пружної деформації зміни форми, яка накопичується в одиниці об'єму. Згідно з енергетичною теорією складний і простий напружений стани є рівнобезпечними, якщо їх питомі потенціальні енергії, пов'язані із змінами форми при деформації, дорівнюють одна одній. Згідно з цією теорією

(4.9)

Енергетична теорія добре узгоджується з даними дослідів для пластичних матеріалів і набула великого поширення в інженерній практиці.

Теорія Мора.

На основі експериментальних досліджень міцності при різних напружених станах для матеріалів, які по різному чинять опір розтяганню і стисканню, Мор одержав для таких матеріалів граничні криві. На основі аналізу цих кривих він одержав вираз для еквівалентного напруження. Умова міцності в даному випадку має вигляд:

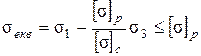(4.10)

де [s]_р і [s]_с - допустимі напруження відповідно при розтяганні і при стисканні.

Теорія Мора тотожна з третьою теорією міцності.

Умовою (4.10) користуються для розрахунку міцності при складному напруженому стані матеріалів, які мають різні граничні напруження при розтяганні і стисканні.

Читайте також:

1. II. Основні закономірності ходу і розгалуження судин великого і малого кіл кровообігу
2. Адвокатура в Україні: основні завдання і функції
3. Амортизація основних засобів, основні методи амортизації
4. Артеріальний пульс, основні параметри
5. Банківська система та її основні функції
6. Біржові товари і основні види товарних бірж. Принципи товарних бірж.
7. Будова й основні елементи машини
8. Будова оптоволокна та основні фізичні явища в оптоволокні.
9. Бюджетування (основні поняття, механізм).
10. Валютний ринок, основи його функціонування. Основні види валютних операцій
11. Варіатори та їхні основні параметри
12. Взаєморозрахунки з контрагентами та податковий облік: основні принципи

Переглядів: 2193