• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Напруження на похилих площадках. Умови на поверхні.

Тензор напружень. Найбільші дотичні напруження.

Головні напруження та головні площадки.

Напруження на похилих площадках. Умови на поверхні.

Для визначення напруженого стану в будь-якій точці тіла крім напружень на площадках, нормальних до координатних осей x, y, z потрібно вміти обчислювати напруження на довільній площадці похилій по відношенню до цих осей.Розглянемо тіло довільного обрису з накладеними на нього опорними в’язями та на яке впливають поверхневі і об’ємні сили. З його об’єму виділимо нескінченно малий об’єм тіла у вигляді паралелепіпеду. В об’ємі паралелепіпеду позначимо похилу площадку abc (рис. 2.1). Положення в просторі нескінченно малої площадки abc визначається нормаллю ν (рис. 2.2), направляючи косинуси якої:

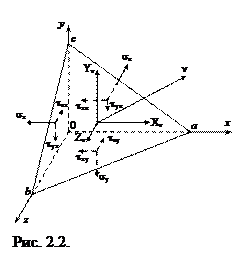
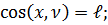
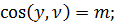
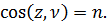
Похила площадка abc разом з координатними площинами Оab, Оbc, Оca утворюють елементарний тетраедр. Позначимо площу грані abc через dA; тоді площа інших граней тетраедра визначимо як проекції площі грані abc на відповідні координатні площини:

Оbc = dA∙ℓ,

Оca = dA∙n,

Оab = dA∙m.

На тетраедр, що розглядається, впливають наступні сили:

- на координатних площадках – сили від шести складових напружень σ_x, σ_y, σ_z, τ_xy, τ_yx, τ_zx;

- на площадці abc – сили від трьох складових повного напруження X_ν, Y_ν, Z_ν;

- за всім об’ємом – складові об’ємної сили X, Y, Z (не показані на рис. 2.2).

Спроектувавши всі сили на вісь x, отримаємо:

.

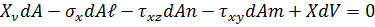В отриманому рівняння остання складова більшого порядку малості (dV-третій) у порівнянні з іншими складовими (dA-другий). Знехтуємо цією складовою, та поділимо кожну складову рівняння на dA, тоді:

.

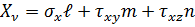Склавши рівняння проекцій на вісі y, z, отримаємо ще два подібних рівняння. Здобуті рівняння, носять назву – рівняння рівноваги елементарного тетраедра і записуються у вигляді:

(2.1)

Рівняння (2.1) дозволяють визначати складові напружень на будь-якій похилій площадці з нормаллю ν за допомогою шести складових напружень на площадках, які паралельні координатним площинам.

Якщо площадка abc співпадає з поверхнею тіла, то складові напруження X_ν, Y_ν, Z_ν відповідають складовим зовнішніх сил, що діють на поверхні тіла, то рівняння (2.1) називають умовами на поверхні тіла. Вони пов’язують між собою зовнішні та внутрішні сили.

Якщо тіло задовольняє рівнянням (1.3) та (2.1), то воно перебуває в стані рівноваги під дією зовнішніх сил. Дійсно, якщо складові напружень (1.6), задовольняють рівнянням рівноваги (1.3) в усіх точках в середині тіла, то всі точки в середині тіла знаходяться в рівновазі. Якщо складові напружень (1.6) задовольняють рівнянням (2.1) в точках біля поверхні тіла, то всі точки біля поверхні знаходяться в рівновазі. Якщо складові напружень (1.6) одночасно задовольняють рівнянням (1.3) та (2.1), то в рівновазі знаходиться все тіло в цілому.

І навпаки, якщо тіло знаходиться в рівновазі під дією заданого зовнішнього навантаження, то в усіх точках в середині тіла повинні перетворюватися на тотожність рівняння (1.3), а в усіх точках на поверхні тіла – рівняння (2.1).

Читайте також:

1. Аналогія як умовивід
2. Блок 4. Умови та охорона праці.
3. Блок перевірки умови
4. БУДОВА ТА УМОВИ ФОРМУВАННЯ ШАРУВАТИХ ТОВЩ
5. Види аудиторських висновків та умови їх надання
6. Види буріння похилих свердловин
7. Види і типи організаційних структур та умови їх ефективного застосування
8. Види й типи організаційних структур та умови їх ефективного застосування
9. Визначення втрат попереднього напруження
10. Визначення зусилля попереднього обтиску і величини попереднього напруження
11. Винесення внутрішніх, розумових дій назовні називають ексте­ріоризацією.
12. Вирішення суперечок між суб'єктами страхування. Умови припинення дії договору.

Переглядів: 1281