• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция

Основні рівняння теорії пружності.

Основні рівняння теорії пружності.

Тема: Рішення задачі теорії пружності.

4.2. Плоска задача теорії пружності в прямокутній системі координат.

На попередніх лекціях були отримані три групи формул, які утворюють основні рівняння теорії пружності.

1. Статичні рівняння. В цю групу входять диференціальні рівняння рівноваги (1.3):

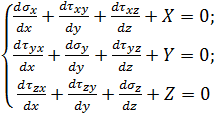(4.1)

та умови на поверхні (2.1):

(4.2)

2. Геометричні рівняння. В цю групу входять геометричні співвідношення Коші (3.10):

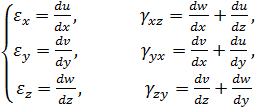(4.3)

та рівняння неперервності деформацій (3.20):

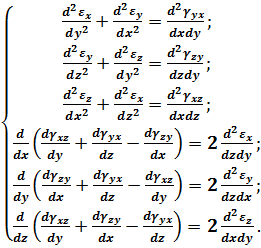(4.4)

3. Фізичні рівняння. В цю групу входять формули закону Гука в прямій (3.21) або оберненій (3.28) формах:

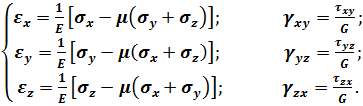(4.5)

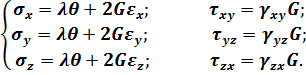(4.6)

Користуючись наведеними залежностями, можна вирішувати задачі торії пружності по визначенню напружень та деформацій, які виникають в пружному тілі під впливом зовнішнього навантаження.

Рівняння налічують 15 невідомих функцій:

- шість складових напружень

- шість складових деформацій

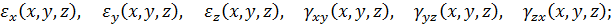
- три складові переміщення

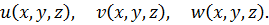
Для визначення цих функцій маємо 15 рівнянь: три диференціальних рівняння рівноваги (4.1), шість геометричних співвідношень Коші (4.3), шість формул закону Гука в прямій (4.5) або оберненій (4.6) формах. Таким чином, з математичної точки зору задача зводиться до інтегрування вказаних 15 рівнянь за умови, що вони задовольняють умовам на поверхні (4.2).

Розв’язок рівнянь можна проводити наступними способами, в залежності від того, які величини прийняті за основні невідомі.

1. Розв’язок в переміщеннях, коли за невідомі прийняті три складові переміщень: .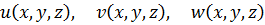

2. Розв’язок в напруженнях, коли за невідомі прийняті шість складових напружень: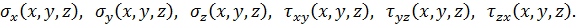

3. Розв’язок в змішаній формі, коли за невідомі прийняті деякі складові переміщень та деякі складові напружень.

Розв’язок в переміщеннях.Для визначення трьох складових переміщень потрібно мати три рівняння, які отримують з диференціальних рівнянь рівноваги (4.1), виразивши в них напруження через переміщення. Скористаємося першим рівнянням (4.1) та підставимо в нього напруження з формул закону Гука (4.6):

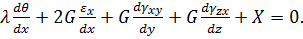
В отримане рівняння підставимо величину деформацій скориставшись для цього формулами (4.3):

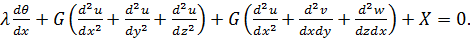
Позначимо вираз в перших дужках наступним чином:

(4.7)

Цей диференціальний оператор називають оператором Лапласа над функцією u(x,y,z) і читається як “набла два u”.

Вираз в других дужках можна перетворити наступним чином:

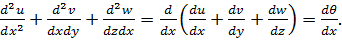
Після згадуваних перетворень початкове рівняння набуває вигляду:

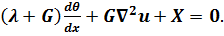
Аналогічно перетворимо і два інших диференціальних рівняння рівноваги (4.1). Після цього отримаємо систему рівнянь для розв’язку задачі теорії пружності в переміщеннях:

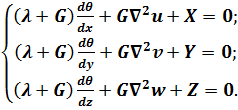(4.8)

Рівняння (4.8) носять назву – рівняння Ламе. Вони поєднують статичні, геометричні та фізичні рівняння теорії пружності. Дійсно, в них присутні умови рівноваги кожного елементу, геометричні характеристики деформацій u, v, w та фізичні характеристики матеріалу λ та G.

Таким же чином перетворимо рівняння умов на поверхні. Для цього в рівняння (4.2) підставимо вираз для обчислення напружень (4.6):

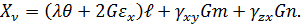
Підставимо в це рівняння величину деформацій (4.3) та згрупуємо всі члени наступним чином:

Вираз в перших дужках представляє собою похідну функції u(x,y,z) за напрямком нормалі ν до поверхні тіла. Дійсно, обчисливши похідну складної функції u(x,y,z) за змінною ν, отримаємо:

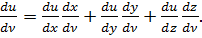
Пригадаємо, що похідні координат за ν представляють собою відповідні направляючи косинуси нормалі ν:

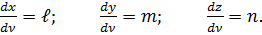
Таким чином,

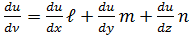
і початкове рівняння набуде вигляду:

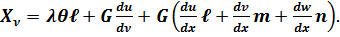(4.9)

Аналогічно можна перетворити два інших рівняння (4.2). При цьому отримаємо наступні три рівняння умов на поверхні, виражені через переміщення:

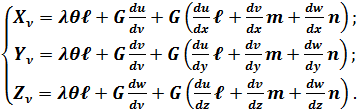(4.10)

Для визначення трьох складових переміщень u, v, w потрібно про інтегрувати три рівняння Ламе (4.8) та задовольнити умовам на поверхні (4.10). За отриманими переміщеннями та геометричними співвідношеннями Коші (4.3) визначають складові деформацій, а потім з формул закону Гука (4.6) – складові напружень.

Розв’язок в напруженнях. Надалі коло розглядуваних задач обмежимо випадками, коли об’ємні сили сталі за всім об’ємом тіла, або дорівнюють нулю. Це обмеження дозволяє значно спростити певні рівняння при розв’язку задачі в напруженнях, оскільки всі похідні від складових об’ємних сил по координатам x, y, z перетворюються на нуль.

При розв’язку задачі теорії пружності в напруженнях за основні невідомі приймають шість складових напруження: Для їх визначення трьох рівнянь рівноваги (4.1) недостатньо і тому потрібно додати ще шість рівнянь неперервності деформацій (4.4). В останні входять складові деформації, які потрібно попередньо виразити через напруження. Зробивши це та провівши ряд спрощень та перетворень отримаємо наступні шість рівнянь:

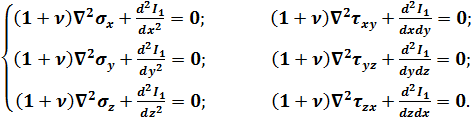(4.11)

Останні рівняння отримані в 1892 р. італійським математиком Е. Бельтрамі. В 1899р. австралієць Дж. Мічел отримав схожі рівняння для випадку, коли об’ємні сили не сталі і, відповідно, в праву частину рівнянь замість нулів входять похідні від об’ємних сил. Тому останнє рівняння називають рівнянням Бельтрамі-Мічела.

Таким чином, для розв’язку в напруженнях потрібно інтегрувати дев’ять рівнянь (4.1) та (4.11). Наявність трьох зайвих рівнянь потрібна для отримання однозначного розв’язку.

Отримані після інтегрування шість складових напружень повинні задовольняти умовам на поверхні (4.2). Після цього за формулами закону Гука (4.5), визначають складові деформацій, а з геометричних співвідношень Коші (4.3) – складові переміщень.

Аналіз наведеного вище дозволяє дійти висновку, що розв’язок задач теорії пружності будь-яким способом зводиться до інтегрування системи диференціальних рівнянь в частних похідних, які визначають поведінку пружного тіла у внутрішніх точках. До цих рівнянь додаються умови на поверхні, що обмежують тіло. Ці умови диктують обмеження щодо зовнішніх поверхневих сил або переміщень точок поверхні тіла. В залежності від цього зазвичай формулюють один з трьох типів краєвих задач.

Перша краєва задача – кінематична. В об’ємі тіла знаходять складові переміщень, які приймають на поверхні певні значення. В умові на поверхні тіла таким чином задаються рівняння поверхні та величини складових переміщень на цій поверхні.

Друга краєва задача - статична. В цьому випадку на поверхні тіла відсутні будь-які обмеження на переміщення і задаються рівняння поверхні, направляючи косинуси нормалі до поверхні та величини складових поверхневого навантаження.

Третя краєва задача – змішана. В цьому випадку на одній частині поверхні тіла задаються кінематичні умови, а на другій – статичні.

Розрізняють три основних метода математичного розв’язку задач теорії пружності:

1. Прямий метод. Він полягає в безпосередньому інтегруванні рівнянь теорії пружності сумісно з заданими умовами на поверхні.

2. Обернений метод. В цьому випадку задаються функціями напружень або переміщень, які задовольняють диференціальним рівнянням, та визначають, яким зовнішнім навантаженням відповідає розглядувана система переміщень чи напружень.

3. Напівобернений метод Сен-Венана. Задається частина функцій напружень або переміщень. Потім за допомогою рівнянь теорії пружності встановлюються залежності, яким повинні задовольняти функції напружень та переміщень що залишились. При цьому відбувається істотне спрощення диференціальних рівнянь. Цей метод є найбільш прийнятним для розв’язку задач теорії пружності.

Для перевірки правильності розв’язання задач теорії пружності використовують наступну теорему – для тіла, що знаходиться в природному стані, розв’язок задачі буде єдиним, якщо продовжує виконуватися принцип незалежності дії сил.

4.2. Плоска задача теорії пружності в прямокутній системі координат.

Розглянемо плоску пластину до якої прикладене зовнішнє навантаження. Будемо вважати, що її товщина дуже мала у порівняння з поперечними розмірами. За таких умов, розглядуване тіло є дуже тонка розтягнута плівка. Виділимо нескінченно малий прямокутний елемент пластини (рис. 4.1). На його гранях, в загальному випадку, виникають напруження σ_x, σ_y, τ_xy = τ_yx = τ. На бокових (заштрихованих) гранях цього елемента напруження відсутні: σ_z = 0, τ_xz = 0, τ_yz =0. Припустимо, що ці напруження дорівнюють нулю і у внутрішніх точках елемента. Описуваний стан називають узагальненим плоским напруженим станом елемента. Він характеризується тим, що дві паралельні грані нескінченно малого елемента, вільні від напружень. Напруження σ_x, σ_y, τ при цьому рівномірно розподілені за товщиною пластини.

Рівняння теорії пружності значно спрощуються для випадку плоского напруженого стану, оскільки задача зводиться до визначення тільки двох змінних. При плоскому напруженому стані, в пружному тілі, переміщення відбуваються тільки паралельно площині xOy:

Підставляючи ці складові переміщень в геометричні співвідношення Коші (4.3), отримаємо:

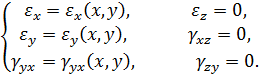(4.12)

Незважаючи на те, що в напрямку осі Oz відсутні лінійні деформації, в цьому напрямку діє напруження σ_z. При цьому елемент перебуває в стані плоскої деформації. Єдина відмінність останнього від узагальненого плоского напруженого стану це те що σ_z ≠0. Напруження σ_z залежать від напружень, що діють в площині xOy. Дійсно, з третьої формули закону Гука (4.5) за відсутності деформації ε_z, отримаємо:

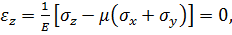
звідки

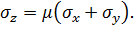(4.13)

Це ж рівняння можна записати наступним чином:

Зважаючи на сказане запишемо основні рівняння теорії пружності для випадку плоского напруженого стану.

Диференціальні рівняння рівноваги (4.1) набувають вигляду:

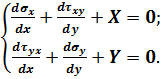(4.14)

Оскільки на боковій поверхні в усіх точках направляючий косинус n = 0, то з рівнянь умов на поверхні (4.2) залишаються тільки два:

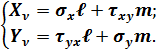(4.15)

Шість геометричних співвідношень Коші (4.3) зводяться до трьох:

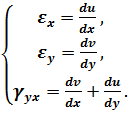(4.16)

З шести рівнянь нерозривності деформацій (4.4) залишається лише тільки одне, а інші перетворюються на тотожність:

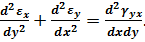(4.17)

З шести формул закону Гука (4.5) залишаються тільки три, які з врахуванням виразів (4.12), (4.13) набувають вигляду :

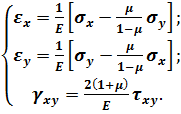(4.18)

Введемо позначення. Нехай 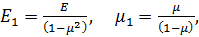тоді формули (4.18) набувають вигляду:

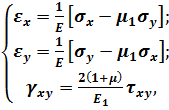(4.19)

при цьому значення коефіцієнта пропорційності в третьому рівнянні не змінюється:

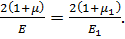
Читайте також:

1. II. Основні закономірності ходу і розгалуження судин великого і малого кіл кровообігу
2. V Процес інтеріоризації забезпечують механізми ідентифікації, відчуження та порівняння.
3. А .Маршалл - основоположник неокласичної теорії.
4. Адвокатура в Україні: основні завдання і функції
5. Аксіоматичний метод у математиці та суть аксіоматичної побудови теорії.
6. Альтернативні теорії вартості
7. Альтернативні теорії капіталу
8. Альтернативні теорії макроекономічного регулювання
9. Альтернативні теорії максимізації
10. Альтернативні уявлення щодо макроекономічного регулювання: теорії раціональних сподівань та економіка пропозиції. Крива Лафера.
11. Амортизація основних засобів, основні методи амортизації
12. Артеріальний пульс, основні параметри

Переглядів: 2542