Лінгвістичне забезпечення АСУТП

Засіб Беллмана

Тема Динамічне програмування

ЛЕКЦІЯ 10

Організаційне забезпечення

Інформаційне забезпечення

Інформаційне забезпечення АСУТП охоплює:

- інформацію, що характеризує стан автоматизованого технологічного комплексу;

- системи класифікації і кодування технологічної і техніко-економічної інформації;

- масиви даних і документів, необхідних для виконання усіх функцій АСУТП, у тому числі нормативно - довідкову інформацію, що забезпечує задане функціонування автоматизованого технологічного комплексу.

Даний вид забезпечення представляється схемами організаційної структури. На цих схемах вказані підрозділи або посадові особи, що забезпечують функціонування АСУТП, або одержують від цієї системи інформацію, а також зв'язки між підрозділами і посадовими особами, зазначеними на схемі і їхня співпідпорядкованість. Ці схеми відбивають структуру керування об'єктом, раціональна форма якої являється результатом аналізу технологічного процесу, транспортних, матеріальних і енергетичних потоків.

Крім схеми організаційної структури, організаційне забезпечення при розробці АСУТП повинно містити наступні поділи:

а) зміни в організаційній структурі керування об'єктом;

б) організація підрозділів;

в) реорганізація існуючих підрозділів керування.

Робоча документація організаційного забезпечення являється експлуатаційною документацією і призначений для опису дій персоналу по забезпеченню функціонування АСУТП. Основними документами при цьому являються:

- технологічні інструкції;

- інструкції з експлуатації;

- посадові інструкції.

10.1 Рішення оптимальних задач за допомогою методу динамічного програмування (засіб Белмана).

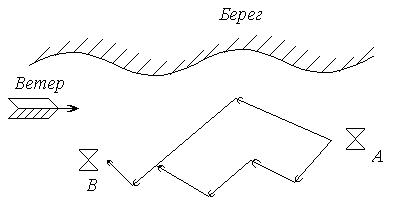Розглянуті вище методи активного експерименту спрямовані, в остаточному підсумку, на визначення екстремумів функцій відгуку, тобто на оптимізацію режимів функціонування автоматизованих технологічних об'єктів. Цій же меті служить так званий метод динамічного програмування (засобу Белмана), суть котрого доцільно роздивитися на прикладі поширеної задачі визначення оптимальної траєкторії руху вітрильних човнів на регатах. Характерною рисою цих змагань є необхідність проходити частину шляху в "лавировку" (галсами) через зустрічний напрямок вітру. Зміна галсів викликає, у свою чергу необхідність поворотів, і, як слідство – втрати часу. Тобто, переходячи на мову технічної кібернетики, тут присутня задача на оптимізацію процесу по швидкодії. Отже, оптимальною траєкторією руху яхти буде така, що потребує найменшого часу на проходження траєкторії між поворотними знаками А і В. Крім досвіду команди, характеру вітрильного судна і т.д. в аналізованому процесі бере участь також зовнішнє середовище, тобто в різних точках простору швидкість і напрямок вітру і течії можуть бути різними. Тому при довгих галсах менше часу витрачається на повороти, але поблизу берега швидкість вітру, звичайно, менша, чим удалині від нього, і траєкторія може виявитися не самою вигідною.

Для рішення даної задачі декілька ідеалізуємо її: будемо вважати, що точки А і В не обминаються, а лише розглядається маршрут А-В. Крім того, при відомих зовнішніх умовах (розподіл швидкостей вітру і течій) реально досяжний час залежить тільки від координат точок А і В, тобто

T=F (XA, YA, XB, YB)

Так як у вихідній задачі число варіантів нескінченно велике, то вибрати найкращий із них, тобто вирішити задачу – практично неможливо. Тому необхідно замінити безупинний простір "квантовим" дискретним, тобто рахуючи, що повороти можуть тільки у визначених точках водяної поверхні.

Припустимо, що, обравши початковий курс АN, можна зробити поворот в однієї з точок а01, а02,…, а0n, тобто утворюється n нових гілок траєкторії, на кожній із яких, наприклад на а0(n-1)_{М, є}також і можливих точок повороту. А з огляду на, що загальне число варіантів складає nn, тобто при n=10 , буде 1010. Щоб оцінити отриманий результат, варто врахувати, що якщо використовувати для обчислення часу, що затрачається на проходження кожного варіанта траєкторії, машину, що виконує одне таке обчислення за 1 із, той загальний час, необхідний для прорахунку усіх варіантів, складе більш 300 років (!),а точніше 317 рік.

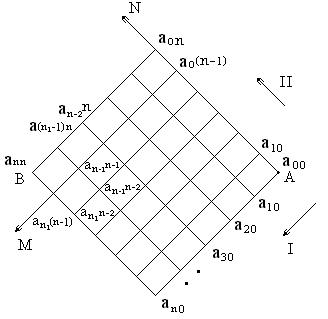
Правда, при n=4 буде потрібно – 256 с., тобто усього трохи більше 4 хвилин, але і це для таких гонок є великою втратою часу, тобто сама ідея рішення задачі шляхом перебору усіх варіантів не є оптимальною. А оптимізувати саме рішення дозволить метод динамічного програмування. Зафіксуємо точку В і почнемо обчислення з точок аn_(n-1) і аn-1, які віддалені від точки В усього на один крок. Обчислення Тn_{, n-1} і Тn-1_,n нескладно, тому що траєкторія переходу з цих точок у точку В – єдина. Тепер переходимо до точок аn_{, n-2}, an-1_,n-1і аn-2_,n, що відстоять від кінцевої на два кроки. Від кожній із них можна перейти до аn_,n-1 або аn-1_,n не більш, чим двома шляхами. Визначивши час, необхідний для цих переходів, неважко знайти й оптимальну траєкторію руху від кожній із цих точок. Переходячи до точок, що відстоять від кінцевої точки на три кроки, помічаємо, що для кожній із цих точок таки необхідно підрахувати не більш двох варіантів, тому що за один крок із цих точок можна потрапити в точки _аn,n-1, _an-1,n-1, _an-2,n, для яких мінімальний час і оптимальні траєкторії уже відомі. Продовжуючи аналогічні міркування крок за кроком, аж до вихідної точки А, ми можемо переконатися, що для кожної нової точки приходиться обчисляти тривалість 1-2х кроків. Тому загальне число кроків обчислюється для поля розділеного сіткою n*n складе усього 2n2, що при n=10 дає тільки 200, а при n=4 усього 32 операції, що можливо навіть вручну. Виграш у часу при використанні методу Белмана пояснюється відкиданням неоптимальних варіантів.

Читайте також:

<== попередня сторінка	\|	наступна сторінка ==>
Класифікація моделей АСУ	\|	Лінгвістичне забезпечення АСУТП

Не знайшли потрібну інформацію? Скористайтесь пошуком google:

Генерація сторінки за: 0.02 сек.