• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Класифікація моделей АСУ

Як відомо, теоретичні дослідження і розрахунки при одержанні моделі АСУ, підтверджуються експериментами. Проте в ряді випадків виконати цю перевірку на натурі не представляється можливим. Наприклад, спроектували електростанцію. Як перевірити правильність розрахунків? Коли побудують перевіряти пізно. Або розробили конструкцію багатомісцевого аеробуса. Як перевірити можливість польоту? Аеродинамічної труби такого великого діаметра немає. Вихід один – необхідно випробувати фізичну модель.

Фізичне моделювання – це моделювання зі зміною масштабу, але зі зберіганням природи явища.

Для того, щоб найбільше повно досліджувати якийсь процес або явище, необхідно мати велику кількість спостережень і вимірів. Виділити головне і глибоко досліджувати процеси або явища за допомогою несистематизованої інформації важко, тому що кожне спостереження або вимір може зафіксувати лише деякі з множини діючих на об'єкт факторів. Тому таку інформацію прагнуть згустити в деяке абстрактне поняття – модель.

Питання подоби явищ розглядаються в рамках теорії подоби, яка базується на трьох теоремах:

1. Два фізичні явища подібні, якщо вони описуються однією і тією ж системою диференціальних рівнянь і мають подібні умови однозначності.

2. Якщо фізичні процеси подібні, то критерії подоби цих процесів рівні між собою.

3. Рівняння, що описують фізичні процеси можуть бути виражені диференціальним зв'язком між критеріями подоби.

Отже модель і оригінал подібні, якщо рівні відповідні критерії подоби.

Крім фізичного є також інші види моделювання, наприклад такі як аналогове і математичне.

Аналоговим називається моделювання зі зміною природи явища, але зі зберіганням його сутності. Це питання вже нами розглядалося при вивченні аналогових ОМ.

Щодо математичного моделювання варто зауважити, що ідентичність математичних виразів процесів оригіналу і моделі ще не означає, що процеси абсолютно аналогічні. Необхідно також враховувати критерії подоби, що отримані через безрозмірні комбінації основних параметрів і кількість яких N = п – 1,

де п – число членів досліджуваного вихідного рівняння.

У ряді випадків зустрічаються процеси, що не можуть бути безпосередньо описані диференційними рівняннями. Залежність між змінними тут можна встановити лише експериментально. У таких випадках для обмеження експерименту та пошуку зв'язку між основними характеристиками процесу можна застосовувати так званий метод аналізу розмірностей, у рамках якого шукані розмірності визначаються на підставі системи рівнянь, що одержуються з умови рівності розмірностей лівої і правої частин рівняння.

Це методи, за допомогою яких установлюють математичні залежнності між параметрами досліджуваного об'єкта.

При цьому широко застосовують:

1) елементарні функції і рівняння, особливо коли прагнуть абстрагувати процес або явище;

2) методи нарисної й аналітичної геометрії;

3) диференціальні рівняння у приватних похідних – при описі теплових, коливальних процесів, течії рідин, дифузії газів і т.д. ;

4) метод варіаційного числення, у рамках якого вводять поняття функціоналу, суть його полягає в слідуючому.

Нехай є плоска крива Y = f (X) із диапазоном визначення X0£ X £X1. Неважко бачити, що довжина кривої L, площа S криволінійної трапеції і обсяг V тіла обертання залежать від виду заданої кривої У = f (X):

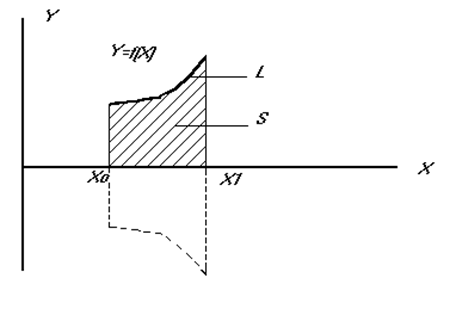
; доб

Таким чином, функція Y = f (X), що однозначно визначає значення L, S і V відіграє роль аргумента, тому величини L, S і V називають функціоналом щодо функції Y = f (X) і записується він таким чином

L, S і V = F {Y= f (X)}

Задача варіаційного числення складається в тому, що якщо заданий функціонал F (Y) у диапазоні Х0£ X £X1, то потрібно знайти таку функцію Y = f (X), при котрій цей функціонал приймав би мінімальне або максимальне значення.

5) У галузі будівельних наук широко використовується теорія функцій комплексної змінної. В основі цієї теорії лежить положення про комфортне перетворення, відповідно до якого можливий, наприклад, переніс двох пересічних кривих Z1Z2 і Z1Z3 із координат Z у координати W1W2 і W1W3, зберігаючи рівність кутів між кривими в кожній парі. Це дозволяє змінити координати таким чином, щоб спростити громіздкі математичні перетворення.

6) При використання складних диференційних рівнянь, або їхніх систем із нелінійними початковими і граничними умовами, прибігають до наближених обчислень за допомогою чисельних методів.

Всі зазначені методи стають більш ефективними при використанні ЕОМ.

У багатьох випадках необхідно досліджувати не тільки детермініровані процеси, для котрих характерною є відповідність кожному значенню аргументу конкретного значення функції, а і випадкові вірогіднісні (стохастичні) процеси, у яких кожному значенню аргументу відповідає безліч значень функції.

Проте, незважаючи на випадковий характер зв'язку, розсіювання має цілком визначені закономірності. Математичною основою цих законів є теорія ймовірності, що базується на таких основних поняттях.

1). Генеральна сукупність N – це нескінчена безліч однорідних подій. Звичайно, на практиці вивчають лише частину генеральної сукупності, що називають вибірковою сукупністю, або малою вибіркою N1.

2). Ймовірність Р (Х) події Х (відносна частота) - це відношення числа випадків N (X), до загального числа подій, тобто

P (X) = N (X)/N;

для достовірної події P(X) = 1;

для неможливої P(X) = 0,

тобто 0 £Pi £1.

3). Математичне чекання m(X) = SXiPi;

4). Розмах варіації ряду подій R = Xmax-Xmin;

5). Дисперсія – характеризує розсіювання випадкового розміру стосовно математичного чекання.

D(X) = S[Xi-m(X)]^2.Pi.

6). Середньоквадратичне відхилення або стандарт – є мірою розсіювання досліджуваного діапазону s(X) = ;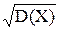

7). Коефіцієнт варіації–дозволяє порівнювати інтенсивності розсіювання в різноманітних сукупностях K = s/m(X).

Середньоквадратичне відхилення s_і –відповідає точкам перегину кривої. Можливість того, що випадкові події не вийдуть за ці межі, дорівнює слідуючим показникам :

±2s – 0,95;

±3s – 0,997;

j=±2/3s – 0,5.

Крім нормального, є також і інші види розподілу: Пуассона, показове, Вейбулла, гама – розподіли, Пірсона, Рэля, бета – розподіли, Шарлье, Гудрига й ін.

До основних ймовірносно-статистичних методів варто віднести дисперсійний і кореляційний аналіз, що поряд з аналізом регресійним ми будемо розглядати при вивченні методів математичної обробки отриманих результатів експерименту.

Для дослідження складних процесів вірогіднісного характеру широко застосовують метод Монте-Карло ( 1950 р.), названий також методом статистичного моделювання, або статичних іспитів. Він базований на використанні випадкових чисел, що моделюють вірогіднісні процеси.

Послідовність рішення задач методом Монте-Карло зводиться до такого:

- збір, обробка й аналіз систематичних спостережень досліджуваного процесу;

- вибір головних і відкидання другорядних факторів;

- упорядкування адекватної математичної моделі;

- побудова графіків і циклограм.

Для рішення задач даним методом необхідно мати статистичний ряд, знати закон його розподілу, середнє значення і дисперсію.

Рішення задач методом Монте-Карло ефективно лише з використанням ЕОМ.

Читайте також:

1. II. Класифікація видатків та кредитування бюджету.
2. V. Класифікація і внесення поправок
3. V. Класифікація рахунків
4. А. Структурно-функціональна класифікація нирок залежно від ступеню злиття окремих нирочок у компактний орган.
5. Адміністративні провадження: поняття, класифікація, стадії
6. АНАЛІЗ ЛІНІЙНИХ МОДЕЛЕЙ ЕКОНОМІЧНИХ ЗАДАЧ
7. Аналіз та синтез моделей систем
8. Аналітичні процедури внутрішнього аудиту та їх класифікація.
9. Банківська платіжна картка як засіб розрахунків. Класифікація платіжних карток
10. Банківський кредит та його класифікація.
11. Банківські ресурси, їх види та класифікація
12. Будівельна класифікація ґрунтів

Переглядів: 739